À-coup
| Unités SI | mètre par seconde cube |
|---|---|
| Dimension | L·T −3 |
| Base SI | m⋅s−3 |
| Nature | Grandeur vectorielle intensive |
| Symbole usuel | j ou J (anglais : jerk, jolt) |
| Lien à d'autres grandeurs | = |
En mécanique, un à-coup, également saccade ou secousse, est une brusque variation du vecteur accélération sans notion de choc, comme un conducteur donnant un coup d'accélérateur, un coup de frein ou un coup de volant.
En physique, le vecteur d'à-coup[1] — en anglais : jerk[2] (pron. /dʒɜːk/, « djeuk ») aux États-Unis ou jolt[2] en Grande-Bretagne — est la dérivée du vecteur accélération par rapport au temps (soit la dérivée troisième par rapport au temps du vecteur position)[3].
L'à-coup est donc un vecteur défini par trois fonctions temporelles — typiquement ses trois composantes selon les axes x, y et z en coordonnées cartésiennes — et il n'existe pas de terme normalisé pour désigner son module que l'on appelle également l'à-coup.
Étymologiquement, les termes jerk et jolt signifient « secousse ».
Le yank (coup sec) est le produit d'une masse par un à-coup (m⋅j), ou de manière équivalente dans le cas d'une masse constante, la dérivée d'une force par rapport au temps.
L'à-coup est donc lié à la vitesse de variation d'une force ou d'un couple. Une personne subissant un à-coup important va le ressentir car elle va avoir du mal à accommoder la force de ses muscles pour maintenir sa posture ; dans un mécanisme, un à-coup important provoque des vibrations. C'est donc un phénomène mesurable, et à prendre en compte du fait de ses conséquences physiques.
L'unité de l'à-coup est le mètre par seconde cube (m⋅s−3). Le symbole utilisé pour l'à-coup n'est pas normalisé, cependant couramment on utilise les notations j ou J (pour jerk ou jolt).
où :
- est l'accélération,
- est la vitesse,
- est la position,
- est le temps.
Importance dans les mécanismes[modifier | modifier le code]


Pour créer une accélération, il faut fournir un effort, selon le principe fondamental de la dynamique. De l'application de cet effort et de la notion d'inertie, il résulte une déformation élastique. Si l'accélération change rapidement, alors la déformation change elle aussi rapidement ; cela entraîne des oscillations dans le système, donc des vibrations.
Exemples
Plus concrètement, prenons l'exemple d'un mobile de masse m poussé par un vérin sur un plan horizontal. Le mouvement se fait sans frottement, la masse de la tige de vérin est négligeable. Nous nous plaçons dans une phase d'accélération uniforme, a est donc constant. Si l'on isole le mobile (en haut dans la figure ci-contre), nous voyons qu'il faut le pousser avec une force
- F = ma.
Si l'on isole le piston, nous voyons que celui-ci subit la poussée du fluide (huile ou air selon le type de vérin), valant F, et l'action du mobile, –F. La tige est donc en compression élastique, elle subit une déformation qui est proportionnelle à l'accélération.
Si l'accélération change lentement (la valeur d'à-coup est faible), alors la longueur de la tige varie progressivement. Mais si l'accélération varie rapidement, la modification de la longueur se propage sous la forme d'une onde de compression. L'adaptation des pièces aux nouvelles sollicitations se fait sous la forme d'oscillations amorties. Cela crée des secousses, des vibrations.

Plaçons-nous maintenant du côté du solide poussé par le vérin. Prenons un solide formé (voir figure ci-contre) :
- d'un bloc parallélépipédique noté 1, de masse m1 ;
- d'une sphère notée 2, de masse m2 ;
- la sphère étant reliée au bloc par une tige de masse négligeable.
Pour accélérer ce système par rapport au sol, il faut fournir une force F valant
- F = (m1 + m2)a.
Le système se déforme alors élastiquement. Cela se comprend bien en se plaçant dans le référentiel lié au système {1 ; 2} (figures de droite) :
- la pièce 1 subit une force d'inertie Fi1 opposée à F, elle est donc en compression ;
- la pièce 2 subit une force d'inertie Fi2 opposée à F, la tige est donc en flexion.
Si l'accélération varie lentement — donc si la valeur d'à-coup est faible —, alors la pièce 1 va se déformer lentement, et la flexion de la tige reliant 2 à 1 va évoluer lentement. Mais si l'accélération varie brutalement — donc si l'à-coup est important —, alors la brusque compression ou détente du bloc 1 va se propager sous la forme d'une onde de compression, et la tige entre 2 et 1 va subir un coup de fouet.
Conclusion
Une valeur d'à-coup importante signifie que l'accélération varie brusquement, donc que la force varie brusquement. On ne peut alors plus considérer que la déformation du système est homogène. Il y a donc des vibrations qui se propagent dans le système. Ces vibrations peuvent créer des dégradations, ainsi que des bruits.
Lorsque l'on conçoit la cinématique d'une machine, par exemple lorsque l'on programme un automate ou que l'on trace le profil d'une came, il faut donc s'attacher à limiter l'à-coup.

Un pic d'à-coup peut également survenir lorsqu'une pièce passe d'une machine à une autre. Dans l'exemple ci-contre, l'objet manutentionné est une barre cylindrique munie d'un col. Lorsque l'objet est sur une roue, il subit une accélération centripète. Lors du passage à la seconde roue, l'accélération centripète change « instantanément » de sens, ou, d'un autre point de vue, la force centrifuge change soudainement de sens. L'objet va donc se mettre à se balancer.
Domaines d'application[modifier | modifier le code]
L'à-coup est régulièrement utilisé dans des domaines tels que l'ingénierie, plus particulièrement dans les secteurs ferroviaires (confort dans les trains, limitation de la brutalité des accélérations et des freinages des métros…) et lors de la conception de montagnes russes et de grands huit. Il est facilement observable en voiture si l'automobiliste ne réduit pas la pression sur les freins à la fin d'un freinage important.
Des objets fragiles ou de précision doivent n'être soumis non seulement qu'à un niveau maximal d'accélération mais également qu'à un niveau maximal d'à-coup ; il en est de même pour les êtres humains (et de manière générale les vertébrés) qui ont besoin de temps pour ressentir les contraintes et adapter en retour leur tension musculaire afin d'y résister dans le but de ne pas subir le coup du lapin. L'à-coup peut également être considéré comme un critère important lorsque les phénomènes de résonances vibratoires sont un problème à prendre en compte.
Lorsqu'un parachutiste est en chute libre à la vitesse terminale (à environ 70 m/s) et qu'il ouvre son parachute en forme d'aile ; durant le processus d'ouverture du parachute, il subira un jerk à peu près constant[4],[5].
Pour les astronautes, la NASA impose un à-coup maximum de 500 g/s (≃ 5 000 m/s3) hors phases de choc[6].
- Panneaux signalant, en France, des situations générant des à-coups sur la route
-
Succession de virages dont le premier est à droite, générant un à-coup latéral.
-
Succession de virages dont le premier est à gauche, générant un à-coup latéral.
-
Panneau avertissant de la présence d'un ralentisseur (à 50m) générant un à-coup vertical.
-
Panneau indiquant la présence d'un ralentisseur générant un à-coup vertical.
Cas du modèle du solide indéformable[modifier | modifier le code]
Si l'on utilise le modèle du solide indéformable pour décrire le comportement d'un système, alors on va parler d'à-coup au sens littéral lorsque l'on a une discontinuité de l'accélération. Si l'on représente graphiquement les composantes du vecteur accélération (ax, ay, az) en fonction du temps, les représentations vont présenter une marche. Les dérivées, qui sont les composantes du vecteur d'à-coup, vont donc prendre une valeur « infinie », un dirac.
Un à-coup au sens littéral correspond donc à une valeur d'à-coup infinie avec le modèle du solide indéformable.
Dans la pratique, les pièces ne peuvent pas changer instantanément de longueur, la valeur de l'à-coup est limitée par le comportement physique du système :
- par le phénomène de sollicitation : rares sont les phénomènes qui changent d'intensité instantanément, il y a dans la plupart des cas une inertie ; par exemple, un moteur ne change pas de régime instantanément mais graduellement, un circuit électrique présente une résistance à la modification de l'intensité (en particulier en présence de bobines d'induction) ;
- par le comportement de la chaîne cinématique : élasticité des pièces, jeu et frottement des liaisons.
Si les vitesses et les charges sont élevées, l'à-coup peut prendre des valeurs extrêmement fortes. Le système va subir des secousses importantes, générant des vibrations donc des bruits et de la fatigue. Par contre, un pic d'à-coup pour des « petits » mécanismes (faibles charges, faibles vitesses) ne pose en général pas de problème en dehors d'un bruit modéré.
Prise en compte dans la conception d'une loi de mouvement[modifier | modifier le code]

Considérons un mouvement rectiligne : un mécanisme doit amener un solide d'une position x = 0 à une position xf.
Solutions simples mais problématiques[modifier | modifier le code]
Loi trapézoïdale en vitesse[modifier | modifier le code]
D'un point de vue cinématique, les lois les plus simples sont :
La solution la plus simple d'un point de vue conceptuel consiste donc à concevoir un mouvement en trois parties :
- Accélération uniforme jusqu'à une vitesse donnée.
- Mouvement uniforme à cette vitesse.
- Décélération uniforme jusqu'à l'arrêt.
Avec une telle cinématique, on voit que l'accélération est une fonction en escalier. Elle n'est pas dérivable aux transitions, l'à-coup est donc infini dans le modèle du solide indéformable.
D'un point de vue concret, une telle loi de mouvement serait réalisée :
- par un système ne permettant pas la régulation de la puissance (« tout ou rien »), comme un vérin hydraulique, pneumatique, ou un moteur dont le circuit d'alimentation n'aurait pour état que « ouvert » ou « fermé », par exemple régulé uniquement par une butée de fin de course ; l'à-coup est alors limité par la vitesse d'ouverture de l'électrovanne, du distributeur ou les propriétés d'amortissement du circuit RLC ;
- par un automate auquel on demanderait d'envoyer instantanément la puissance maximale dans les actionneurs, ce qui ne serait pas raisonnable ; l'à-coup serait alors limité par la vitesse de montée en puissance de l'ensemble ;
- par une came ; on ne peut pas détecter « à l'œil » un problème d'à-coup « infini », puisqu'un humain ne détecte pas une discontinuité de courbure, mais seulement une discontinuité de pente. En effet la came peut paraître « suffisamment lisse » mais néanmoins avoir une dérivée seconde discontinue. C'est le cas de la loi trapézoïdale en vitesse qui produit un profil de came apparemment lisse (cf. le premier chronogramme de la figure Chronogrammes d'un mouvement ayant un profil de vitesse trapézoïdal), mais qui présente une courbure et donc une accélération discontinues (cf. le troisième chronogramme). Autrement dit une discontinuité de courbure n'est pas observable par un humain ; le risque est donc bien réel de concevoir un tel système.

Came à raccordements circulaires[modifier | modifier le code]
Considérons maintenant la conception d'une came : la pièce à faire bouger est sur un chariot coulissant selon l'axe x, et la came est sur un chariot coulissant selon l'axe y à une vitesse constante par rapport au bâti. Le galet suiveur est dans un « couloir », une rainure creusée dans la came. Lorsque le chariot de la came avance en y, le galet suiveur est entraîné par la rainure et le chariot de la pièce avance en x.
Le profil de la came correspond au profil de la courbe x(t). Cette courbe comprend trois parties rectilignes : une partie horizontale (x = 0) correspondant la position initiale, une partie inclinée correspondant au mouvement, et une partie horizontale (x = xf) correspondant à la position finale. La rainure de la came possède donc également trois parties rectilignes.
Le plus simple à dessiner consiste à raccorder ces trois portions rectilignes par des arcs de cercle tangents dont le rayon extérieur est supérieur au rayon du galet. La loi x(t) va donc également avoir des raccordements en « cercle » (ou plutôt en ellipse, selon les échelles de temps et de position adoptées).
On peut voir tout de suite que dans la partie circulaire, le galet subit une accélération centripète/force centrifuge ; on a donc au démarrage et au freinage un passage brutal d'une situation où l'on n'a pas d'accélération (parties linéaires, le galet est immobile ou en mouvement rectiligne uniforme) à une situation avec une accélération non nulle (centripète).
Pour être plus précis, dans la partie circulaire, le centre du galet subit une accélération radiale valant
- a0 = v2/R,
v étant la vitesse relative du centre du galet par rapport à la came et R le rayon de la trajectoire du galet. Ainsi, l'accélération passe « instantanément » de 0 (vecteur vitesse constamment nul à l'attaque de la came) à une valeur a0 (début de la partie circulaire). Et lorsque le galet quitte la partie circulaire, l'accélération radiale cesse tout aussi brutalement.
Voyons ceci sous l'angle des lois de mouvement. Considérons le démarrage : la loi x(t) est l'équation cartésienne d'un cercle passant par les points (0, 0) — point le plus bas du cercle — et (τ, x0) — point le plus à droite. On a donc :
et l'on a donc :

On voit que la vitesse tend vers +∞ lorsque t se rapproche de τ. Cela correspond à la situation où le tracé de la came fait un quart de tour : l'effort de poussée se retrouve perpendiculaire à la trajectoire imposée par le guide du chariot, provoquant une situation de blocage. Cette phase se termine donc pour une valeur de temps t1 strictement inférieure à τ. Au-delà, la came a un tracé rectiligne, cela signifie que la vitesse est constante :
On voit ici que l'on a une rupture de pente de la loi v(t), donc une discontinuité de l'accélération au début et à la fin de la partie circulaire.
Ceci est confirmé par le calcul de l'accélération, qui montre deux discontinuités : une en 0 et une en t1
Nous avons donc là encore un à-coup infini (dirac) à deux instants. La conception de cette came n'est donc pas satisfaisante du point de vue des secousses. Entre ces deux diracs, l'à-coup vaut
Solutions ayant un à-coup fini[modifier | modifier le code]
Pour être sûr d'avoir un à-coup fini (sans pic de dirac), il faut s'assurer que l'accélération soit continue. Il faut donc définir la loi à partir d'un profil d'accélération continu (mais pas nécessairement dérivable), puis l'intégrer pour avoir le profil de vitesse puis enfin le profil de déplacement. Dans la conception d'une came, cela revient à s'assurer de la continuité de la courbure : une courbure continue permet d'avoir une accélération radiale continue, sans variation brusque.
Pour l'accélération, on prend en général des lois simples par partie, par exemple :
- linéaire ;
- sinusoïdale ;
- polynomiale.
Limite d'à-coup et filtre d'à-coup linéaire[modifier | modifier le code]
Si le mouvement est géré par un automate programmable, il est possible de lui faire générer des lois de mouvement en limitant les dérivées de la position, c'est-à-dire en imposant une vitesse, une accélération et un à-coup maximum[7].
La manière la plus simple consiste à avoir un à-coup en escalier, c'est-à-dire pouvant prendre trois valeurs, jmax, 0 et –jmax. On a donc nécessairement une loi d'accélération en trapèze. Si le mouvement est court, alors
- soit l'accélération maximale n'est jamais atteinte, et l'on a donc une loi d'accélération triangulaire, les phases de montée et de descente de la vitesse ne présentent pas de partie rectiligne ;
- ou bien la vitesse maximale n'est jamais atteinte, la loi de vitesse ne présente pas de plateau au milieu ;
- et si le mouvement est très court, ni la vitesse, ni l'accélération maximale ne sont atteintes.
Une autre manière de faire consiste à limiter la vitesse et l'accélération, mais d'appliquer un filtre linéaire à l'à-coup, typiquement un filtre passe-bas pour éviter que l'à-coup ait des variations brusques. Ce procédé permet de modifier la loi de mouvement à la volée, par exemple si l'on change la position finale en cours de mouvement (suivi d'une cible mouvante). Selon la puissance du filtre, cela revient à limiter une dérivée d'ordre supérieur de la position.
Dérivées de l'à-coup[modifier | modifier le code]
Les dérivées du vecteur position d'ordres supérieurs à 3, qui sont donc elles-mêmes des dérivées de l'à-coup, existent également, les fonctions temporelles mécaniques étant toutes dérivables par partie.
Au cours du développement du télescope spatial Hubble et notamment de ses systèmes asservis de contrôle d'orientation, la dérivée quatrième du vecteur position a été utilisée et les ingénieurs ont employé le terme jounce dans leurs publications pour la désigner. Le terme snap est aussi utilisé.
Ces dérivées d'ordre supérieur n'ont pas de sens physique particulier, mais sont des manières de générer une loi de mouvement limitant vitesse, accélération et à-coup.
À-coup angulaire[modifier | modifier le code]


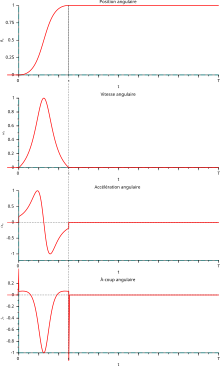
Considérons un mouvement de rotation autour d'un axe fixe dans le référentiel. L'orientation du solide peut s'exprimer par un angle θ (en radians), la position angulaire, à partir duquel on peut exprimer :
- la vitesse angulaire ω (en radians par seconde), sa dérivée temporelle ;
- l'accélération angulaire α (en radians par seconde au carré), la dérivée temporelle de ω.
On peut de même dériver α par rapport au temps et ainsi définir un à-coup angulaire ja :
- ;
- .
L'accélération angulaire implique un couple et donc une torsion du système. Un à-coup important implique une variation brusque du couple, et donc la propagation d'une onde de cisaillement dans le système.
Dans le cas d'un mouvement dans l'espace, on peut modéliser le déplacement d'un solide indéformable par un torseur cinématique, et donc définir à chaque instant un vecteur vitesse de rotation . On peut à partir de là définir un vecteur accélération angulaire
et ainsi un vecteur d'à-coup angulaire
- .
Considérons par exemple une croix de Malte, un dispositif permettant de créer une rotation intermittente de la roue menée à partir d'une rotation continue de la roue menante. Sur un cycle, on a donc une variation de la position angulaire θ durant un quart du cycle, et une position angulaire constante sur le reste du cycle.
Ce dispositif engendre une discontinuité de l'accélération angulaire α, et donc un à-coup angulaire « infini » (dirac), générant une secousse.
Cela n'empêche pas le mécanisme d'être utilisé dans les projecteurs de cinéma à pellicule avec une très grande fiabilité (une très grande durée de vie) et juste un léger bruit, puisque les charges sont très faibles — le système sert à entraîner la partie de la pellicule située dans le couloir de projection, donc une très faible inertie (un film plastique d'une vingtaine de centimètres de long, de quelques dixièmes de millimètre d'épaisseur et de 35 mm de large), peu de frottements, et une vitesse modérée (2,4 m/s, 8,6 km/h).
Pour éviter ce problème d'à-coup, on peut utiliser à la place un dispositif à cames conjuguées comme la double came de Trézel, plus volumineux et plus cher, mais plus silencieux également.
Notes et références[modifier | modifier le code]
- « La cinématique de l’ascenseur décrit le mouvement d’une cabine d’ascenseur dans une cage, en l’absence de masse ou de force. Il s’agit de trouver l’accélération maximale et l’à-coup (modification de l’accélération) pouvant être supportés sans gêne par les passagers, en vue de garantir le meilleur confort possible. » « Rapport de gestion 2002 », sur Groupe Schindler, 2002, p. 68.
- Gibbs et coll. 1998.
- « dérivée troisième », sur forums.futura-sciences.com (consulté le ).
- (en) Theo W. Knack, « Parachute Recovery Systems Design Manual » (consulté le ), p. 5-49.
- (en) Jean Potvin, « Universality Considerations for Graphing Parachute Opening Shock Factor Versus Mass Ratio », Journal of Aircraft, Aerospace Research Central, vol. 44, no 2, , p. 529-533 (DOI 10.2514/1.24061)
- Kathryn L. Lueders, ISS Crew Transportation and Services Requirements Document, NASA, (présentation en ligne, lire en ligne [PDF]).
- [PDF] (en) Peter M. Thompson, « Snap, Crackle, and Pop », sur AIAA (American Institute of Aeronautics and Astronautics.
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) David Eager, Ann-Marie Pendrill et Nina Reistad, « Beyond velocity and acceleration : jerk, snap and higher derivatives », European Journal of Physics, vol. 37, no 6, , article no 065008 (OCLC 6879306577, DOI 10.1088/0143-0807/37/6/065008, Bibcode 2016EJPh...37f5008E, résumé, lire en ligne
 [PDF]).
[PDF]). - Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Supérieur, hors coll., , 4e éd. (1re éd. mai 2008), X-956 p., 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, BNF 45646901, SUDOC 224228161, présentation en ligne, lire en ligne), s.v. jerk, p. 402, col. 1-2.
Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- [Gibbs et coll. 1998] (en) Philip Gibbs, Stephanie Gragert et PEG, « What is the term used for the third derivative of position? », sur FAQ Usenet Physics, 1996-1998 (consulté le ) — Description de l'à-coup

































