Raisonnement diagrammatique
Le raisonnement diagrammatique est un raisonnement au moyen de représentations visuelles. L'étude du raisonnement diagrammatique porte sur la compréhension des concepts et des idées, visualisés à l'aide de diagrammes et d'images plutôt que par des moyens linguistiques ou algébriques.
Thèmes apparentés
[modifier | modifier le code]Caractéristique universelle
[modifier | modifier le code]La caractéristique universelle (en latin : characteristica universalis) est un langage formel et universel imaginé par le philosophe et mathématicien allemand Gottfried Wilhelm Leibniz capable d'exprimer aussi des concepts mathématiques, que scientifiques ou encore métaphysiques. Leibniz espérait ainsi créer un langage utilisable dans le cadre du calcul logique universel mécanisable : le calculus ratiocinator.
Puisque la caractéristique universelle est schématique et emploie des pictogrammes, les schémas des travaux de Leibniz justifient une étude rigoureuse. Leibniz a pu à deux reprises illustrer son raisonnement philosophique avec des diagrammes. Un diagramme, le frontispice de son De arte combinatoria (1666), représente la théorie aristotélicienne selon laquelle toutes les choses matérielles sont formées à partir des quatre éléments : terre, eau, air et feu.
Diagramme
[modifier | modifier le code]Un diagramme est une représentation symbolique géométrique en 2D d'informations selon une technique de visualisation. Parfois, la technique utilise une visualisation en 3D qui est ensuite projetée sur une surface 2D. Le terme diagramme dans le sens commun peut avoir deux significations.
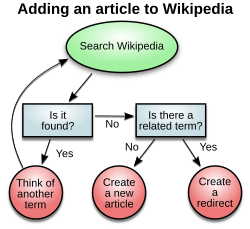
- dispositif d'information visuelle: Comme le terme «illustration», le diagramme est utilisé comme un terme permanent pour toute la classe des genres techniques, incluant les graphiques, dessins techniques et les tableaux[1].
- type spécifique de visualisation: C'est seulement le genre, qui montre des données qualitatives avec des formes qui sont reliées par des lignes, des flèches ou d'autres liens visuels.
En science, vous trouverez le terme utilisé dans les deux sens. Par exemple Anderson (1997) a déclaré que les «diagrammes sont picturaux, mais abstraits, ils représentent l'information. Les graphiques linéaires, blueprints, ou encore les esquisses d'architectes sont tous des exemples de diagrammes, alors que la photo et la vidéo ne le sont pas»[2]. D'autre part Lowe (1993) schémas définis comme des «représentations graphiques abstraites de l'objet qu'ils représentent»[3].
Les bases d'un diagramme peuvent être considérés comme[1]:
- une forme de dispositifs de mise en forme visuelle
- un affichage qui ne montre pas de données quantitatives, mais plutôt des relations et des informations abstraites
- un ensemble de blocs de construction tels que des formes géométriques qui sont connectées par des lignes, des flèches ou autres liens visuels.
Ou selon les mots de Hall (1996), les «diagrammes sont des figures simplifiées, des caricatures, destinés à transmettre une signification essentielle»[4]. selon Jan V. White (1984) «les caractéristiques d'un bon diagramme sont l'élégance, la clarté, la facilité, le motif, la simplicité, et la validité»[1]. L'élégance pour White signifie que ce qui est présent dans le diagramme est «la solution la plus simple et la plus appropriée à un problème»[5].
Graphe logique
[modifier | modifier le code]Un graphe logique est un type particulier de structure graphique-théorétique dans l'une de plusieurs systèmes de syntaxe graphique que Charles Sanders Peirce a développé pour la logique.
Dans ses articles sur la logique qualitative, graphiques entitatifs et graphiques existentiels, Peirce a développé plusieurs versions d'un formalisme graphique ou d'un langage formel graph-théorétique, conçus pour être interprétés en logique.
Graphe conceptuel
[modifier | modifier le code]Un graphe conceptuel est une notation en logique basée sur les graphes existentiels de Charles Sanders Peirce et les réseaux sémantiques de l'intelligence artificielle. Dans le premier article publié sur les graphes conceptuels, John F. Sowa les a utilisés pour représenter les schémas conceptuels utilisés dans les systèmes de base de données.Son premier livre[6] les a appliqué à un large éventail de sujets en intelligence artificielle, informatique et en sciences cognitives. Une notation linéaire, appelée Conceptuel Graphique Interchange Format (CGIF), a été normalisé dans la norme ISO pour la logique commune.
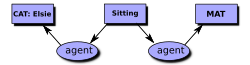
Le diagramme de droite est un exemple de la forme d'affichage d'un graphe conceptuel. Chaque boîte est appelé un nœud de concept, et chaque ovale est appelé un nœud de relation. En CGIF, ce graphe conceptuel serait représenté par la déclaration suivante:
- [Chat Elsie] [Assis *x] [Tapis *y] (agent ?x Elsie) (location ?x ?y)
En CGIF, les crochets entourent l'information à l'intérieur des nœuds de concept, et les parenthèses entourent les informations à l'intérieur des nœuds de relation. Les lettres x et y, qui sont appelés les coreferences labels, montrent comment les nœuds concepts et de relations sont connectés. Dans le Common Logic Interchange Format (CLIF), ces lettres sont mappés à des variables, comme dans la déclaration suivante:
- (existe ((x Assis) (y Tapis)) (et (Chat Elsie) (agent x Elsie) (location x y)))
Graphe existentiel
[modifier | modifier le code]Un graphe existentiel est un type de notation diagrammatique ou visuelle pour des expressions logiques, proposées par Charles Sanders Peirce, qui a écrit son premier article sur la logique graphique en 1882 et a continué à développer cette méthode jusqu'à sa mort en 1914. Peirce proposé trois systèmes de graphes existentiels :
- alpha – isomorphique pour le calcul des propositions et l'algèbre booléenne à deux éléments;
- beta – isomorphique pour la logique du première ordre avec toutes les formules fermées;
- gamma – isomorphique pour la logique modale normale.

En alpha, la syntaxe est:
- La page blanche;
- Lettres seules ou phrases écrites sur la page;
- Tout graphe peut être délimitée par une courbe fermée simple appelé une coupe. Une coupe peut être vide. Les coupes ne doivent jamais se croiser.
Toute partie bien formé d'un graphe est un sous-graphe.
La sémantique est:
- La page blanche représente la Vérité;
- Les lettres, phrases, sous-graphes et les graphes entiers peuvent être Vrai ou Faux;
- Pour joindre un sous-graphe avec une coupe est équivalente à la négation logique.Par conséquent, une coupe vide indique le Faux;
- Tous les sous-graphes avec une coupe donnée sont tacitement conjoints.
Par conséquent, les graphes alpha sont une notation minimaliste pour la logique propositionnelle, fondée sur l'adéquation expressive du Et et du Non.
Notes et références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Diagrammatic reasoning » (voir la liste des auteurs).
- Lee E. Brasseur, Visualizing technical information : a cultural critique, Amityville, N.Y., Baywood Pub, , 161 p. (ISBN 0-89503-240-6)
- Michael Anderson (1997).
- Richard K. Lowe, « Diagrammatic information: techniques for exploring its mental representation and processing », Information Design Journal, vol. 7, no 1, , p. 3–18 (DOI 10.1075/idj.7.1.01low)
- Bert S. Hall (1996).
- Jan V. White, Using charts and graphs : 1000 ideas for visual persuasion, New York, Bowker, , 202 p. (ISBN 0-8352-1894-5)
- John F. Sowa (1984).
