Table de hachage
Une table de hachage est, en informatique, une structure de données qui permet une association clé–valeur, c'est-à-dire une implémentation du type abstrait tableau associatif. Son but principal est de permettre de retrouver une clé donnée très rapidement, en la cherchant à un emplacement de la table correspondant au résultat d'une fonction de hachage calculée en O(1). Cela constitue un gain de temps très important pour les grosses tables, lors d'une recherche ou d'un besoin d'accès aux données en utilisant la clé définie.
Il s'agit d'un tableau ne comportant pas d'ordre (contrairement à un tableau ordinaire qui est indexé par des entiers). On accède à chaque valeur du tableau par sa clé, qui, transformée par une fonction de hachage en une valeur de hachage (un nombre), indexe les éléments de la table, ces derniers étant appelés alvéoles (en anglais, buckets ou slots).
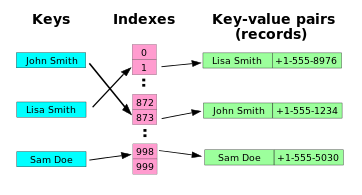
Le fait de créer une valeur de hachage à partir d'une clé peut engendrer un problème de collision, c’est-à-dire que deux clés différentes, voire davantage, pourront se retrouver associées à la même valeur de hachage et donc à la même alvéole (les fonctions de hachage ne sont pas injectives). Pour diminuer les risques de collisions, il faut donc premièrement choisir avec soin sa fonction de hachage. Ensuite, un mécanisme de résolution des collisions sera à implémenter si nécessaire. Il faudra alors stocker dans les alvéoles la paire clé–valeur et pas uniquement la valeur, afin de pouvoir comparer la clé avec celle qui sera donnée en entrée.
Tout comme les tableaux ordinaires, les tables de hachage permettent un accès en O(1) en moyenne, quel que soit le nombre de paires clé–valeur dans la table. Toutefois, comme plusieurs paires clé–valeur peuvent se trouver dans la même alvéole, le temps d'accès dans le pire des cas peut être de O(n). Comparées aux autres tableaux associatifs, les tables de hachage sont surtout utiles lorsque le nombre de paires clé–valeur est très important[réf. nécessaire].
La position des paires clé–valeur dans une table de hachage est pseudo-aléatoire mais dépend de la fonction de hachage choisie et des clés utilisées. Cette structure n'est donc pas adaptée au feuilletage (browsing) de données voisines. Des types de structures de données comme les arbres équilibrés, généralement plus lents (en O(log n)) et un peu plus complexes à implémenter, maintiennent une structure ordonnée.
Fonction de hachage[modifier | modifier le code]
L'idée générale de la fonction de hachage est de répartir les paires clé–valeur dans un tableau d'alvéoles. Une fonction de hachage permet de transformer une clé en une valeur de hachage, donnant ainsi la position d'une alvéole dans le tableau.
Le calcul de la valeur de hachage se fait parfois en deux temps :
- Une fonction de hachage particulière à l'application est utilisée pour produire un nombre entier à partir de la clé ;
- Ce nombre entier est converti en une position possible de la table, en général en calculant le reste modulo la taille de la table.
Si la clé n'est pas un entier naturel, il faut trouver un moyen de la considérer comme tel. Par exemple, si la clé est une chaine de caractères, on peut prendre les valeurs numériques (ASCII ou autre) de chaque caractère et les combiner par une fonction rapide comme le ou exclusif, donnant un entier qui servira d'index. Dans la pratique, on cherche à éviter le recours aux divisions à cause de leur relative lenteur sur certaines machines.
Choix d'une fonction de hachage[modifier | modifier le code]
Une bonne fonction de hachage est utile aux performances, surtout si les collisions sont résolues ensuite par des explorations séquentielles : toute fonction de hachage provoquant beaucoup de collisions (par exemple la fonction qui à une clé associe la valeur ASCII de son premier caractère) ralentira nettement la recherche. Un bon compromis est à trouver entre :
- la rapidité de la fonction de hachage ;
- la taille à réserver pour l'espace de hachage ;
- la réduction du risque des collisions.
Un ou exclusif de tous les caractères d'une clé fournissait souvent un compromis acceptable dans l'écriture de compilateurs au début des années 1960.
Larry Wall utilisa pour implémenter son langage Perl une fonction permettant de doubler autant de fois que nécessaire avec l'extension du nombre de clés l'espace de hachage, sans autre nouveau calcul des clés qu'une translation binaire. [pas clair] [réf. nécessaire]
Les tailles des tables de hachage sont souvent des nombres premiers[réf. nécessaire], afin d'éviter les problèmes de diviseurs communs, qui créeraient un nombre important de collisions. Une autre possibilité est d'utiliser une puissance de deux, ce qui permet de réaliser l'opération modulo par de simples décalages, et donc de gagner en rapidité.
Un problème fréquent est le phénomène de grumelage (clustering) qui désigne le fait que des valeurs de hachage se retrouvent côte à côte dans la table, formant des « grumeaux ». Cela pénalise ces méthodes. Les fonctions de hachage réalisant une distribution uniforme des valeurs de hachage sont à rechercher, mais dès lors que le nombre de clés devient voisin du tiers de la taille de la table ces collisions deviennent probables[note 1].
Quand un attaquant essaye de pénaliser la recherche en soumettant des clés générant un grand nombre de collisions afin de la ralentir (voire de provoquer un déni de service), une solution possible est de choisir aléatoirement une fonction de hachage au début du programme. L'adversaire n'a alors pas de moyen de connaître le type de données qui produira des collisions. Dans la pratique, les algorithmes sont le plus souvent conçus pour affronter des données réparties de manière aléatoire que contre un adversaire.[réf. nécessaire]
Fonction de hachage parfaite et minimale[modifier | modifier le code]
Une fonction de hachage est dite parfaite si elle n'engendre aucune collision. Si toutes les clés sont connues, une fonction de hachage parfaite peut être utilisée pour créer une table de hachage parfaite sans aucune collision.
Une fonction de hachage est dite minimale si elle est parfaite et répartit n entrées dans une table de exactement n alvéoles.
Une fonction de hachage parfaite permet un accès en temps constant dans tous les cas.
Facteur de compression[modifier | modifier le code]
Le facteur de compression (load factor) qui est la proportion d'alvéoles utilisées dans une table de hachage est une indication critique de ses performances.
Il est défini ainsi :
où
- n est le nombre de paires clé–valeur ;
- k est le nombre d'alvéoles.
Modification de la taille de la table[modifier | modifier le code]
Lorsque le facteur de compression de la table augmente au-delà de 50 %, les collisions deviennent fréquentes. Une solution est d'augmenter la taille de la table (c'est-à-dire le nombre d'alvéoles) sitôt atteint ce taux, tout en maintenant cette taille à un nombre premier ou à une puissance de 2 selon que l'on travaille par division (lent) ou modulo (bien plus rapide). S'il y a des dizaines de milliers de clés ou davantage, le calcul d'une nouvelle valeur doit être aussi rapide que possible — il doit si possible se déduire à partir de la clé antérieure, idéalement par simple décalage binaire (shift).
Le rehachage (rehash) est une fonction qui, en général, double (au moins) l'espace mémoire alloué pour la table, et recopie parfois ses valeurs (temps d'exécution en O(n)). Cette fonction cherche le plus petit nombre premier supérieur à deux fois sa taille.
Dans la pratique, les fonctions idéales dépendent des progrès relatifs des vitesses de calcul des processeurs et des temps d'accès à la mémoire : des choix bien adaptés à une génération de machines pourront ne plus l'être pour la suivante.
Résolution des collisions[modifier | modifier le code]
Lorsque deux clés ont la même valeur de hachage, les paires clé–valeur associées sont stockées dans la même alvéole. On doit alors employer une méthode de résolution des collisions.
Le calcul probabiliste montre que même si la fonction de hachage a une distribution parfaitement uniforme, il y a 95 % de chances d'avoir une collision dans une table de hachage à 1 million d'alvéoles avant même qu'elle ne contienne 2 500 paires clé–valeur. Les collisions ne posent cependant de réel problème que si elles sont nombreuses au même endroit. Même une collision unique sur chaque clé utilisée n'a pas d'effet très perceptible.
Plusieurs méthodes de traitement des collisions existent. Les plus utilisées sont le chaînage et l'adressage ouvert. Depuis le début des années 1990, les développeurs de logiciels n'ont plus à se préoccuper vraiment du détail de ces méthodes, celles-ci étant directement incorporées dans les langages eux-mêmes — Perl, PHP, REXX, etc. — ou au pire dans les objets de la bibliothèque qu'ils utilisent.
Chaînage[modifier | modifier le code]
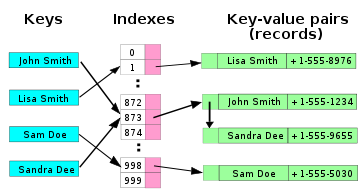
Cette méthode est la plus simple. Chaque alvéole de la table est une liste chaînée des paires clé–valeur qui ont la même valeur de hachage. Une fois l'alvéole trouvée, la recherche est alors linéaire en la taille de la liste chaînée. Dans le pire des cas où la fonction de hachage renvoie toujours la même valeur de hachage quelle que soit la clé, la table de hachage devient alors une liste chaînée, et le temps de recherche est en O(n). L'avantage du chaînage est que la suppression d'une clé est facile, et que l'agrandissement de la table peut être retardé plus longtemps que dans l'adressage ouvert, les performances se dégradant moins vite.
D'autres structures de données que les listes chaînées peuvent être utilisées. En utilisant un arbre équilibré, le coût théorique de recherche dans le pire des cas est en O(log n). Cependant, la liste étant supposée être courte, cette approche est en général peu efficace à moins d'utiliser la table à sa pleine capacité, ou d'avoir un fort taux de collisions. Un tableau dynamique peut aussi être utilisé pour réduire la perte d'espace mémoire et améliorer les performances du cache lorsque le nombre de paires clé–valeur est petit.
Adressage ouvert[modifier | modifier le code]

L'adressage ouvert consiste dans le cas d'une collision à stocker les paires clé–valeur dans d'autres alvéoles. La position des alvéoles est déterminée par une méthode de sondage. Lors d'une recherche, si l'alvéole obtenue par hachage direct ne permet pas d'obtenir la bonne clé, une recherche sur les alvéoles obtenues par une méthode de sondage est effectuée jusqu'à trouver la clé, ou non, ce qui indique qu'aucune clé de ce type n'appartient à la table.
Les méthodes de sondage courantes sont :
- le sondage linéaire : l'intervalle entre les alvéoles est fixe, souvent 1 ;
- le sondage quadratique : l'intervalle entre les alvéoles augmente linéairement (les indices des alvéoles augmentent donc quadratiquement), ce qui peut s'exprimer par la formule : où k est le nombre d'alvéoles.
- le double hachage : l'indice de l'alvéole est donné par une deuxième fonction de hachage, ou hachage secondaire.
Le sondage linéaire possède la meilleure performance en termes de cache, mais est sensible à l'effet de grumelage décrit plus haut. Le double hachage ne permet pas d'utiliser le cache efficacement, mais permet de réduire presque complètement ce grumelage, au prix d'une complexité plus élevée. Le sondage quadratique se situe entre le linéaire et le double hachage au niveau des performances.
Plus le facteur de compression est proche de 100 %, plus le nombre de sondages à effectuer devient important. Lorsque la table est pleine, les algorithmes de sondage peuvent même échouer. Le facteur de compression est en général limité à 80 %, même en disposant d'une bonne fonction de hachage.
Des facteurs de compression faibles ne sont pas pour autant synonymes de bonnes performances, une mauvaise fonction de hachage pouvant générer un grumelage. L'indexation par la valeur ASCII du premier caractère d'une variable laisserait par exemple nombre de cases inutilisées, tout en assurant un maximum de collisions sur des noms de variables tels que x1, x2, … en calcul scientifique ou sur des prénoms répandus tels que Martin, Michel, … en traitement d'annuaires.
Hachage probabiliste[modifier | modifier le code]
Notes et références[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Donald E. Knuth, The Art of Computer Programming, vol. 3 : Sorting and Searching, , 2e éd. [détail de l’édition], partie 6, chap. 4 (« Hashing »), p. 513-558
- (en) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique [« Introduction to Algorithms »], MIT Press et McGraw-Hill, , 2e éd., 1180 p. (ISBN 978-0-262-03293-3, lire en ligne), chap. 11 (« Hash Tables »), p. 221-252
- (en) Michael T. Goodrich (en) et Roberto Tamassia (en), Data Structures and Algorithms in Java, John Wiley & Sons, , 4e éd., 720 p. (ISBN 978-0-471-73884-8), chap. 9 (« Maps and Dictionaries »), p. 369-418
- Christine Froidevaux, Marie-Claude Gaudel et Michèle Soria, Types de données et algorithmes, McGraw-Hill, coll. « Informatique », , 575 p. (ISBN 978-2-84074-023-0)
Références[modifier | modifier le code]
Notes[modifier | modifier le code]
Article connexe[modifier | modifier le code]
- Filtre de Bloom, une autre structure de données fondée sur les fonctions de hachage



