Méthode de Box-Muller

Représentation graphique de la transformation : les cercles de départ, répartis uniformément autour de l'origine, deviennent un nouvel ensemble de cercles centrés, dont la répartition est proche de l'origine puis s'étiole rapidement. Les plus grands cercles de départ correspondent aux plus petits cercles d'arrivée, et vice-versa.

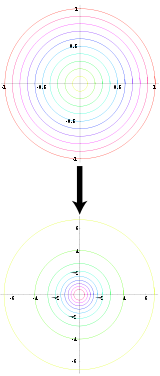
En théorie des probabilités et en informatique, la méthode de Box-Muller (George E. P. Box et Mervin E. Muller, 1958) consiste à générer des paires de nombres aléatoires à distribution normale centrée réduite, à partir d'une source de nombres aléatoires de loi uniforme.

La transformation prend communément deux formes.

• La forme « simple » transforme des coordonnées polaires uniformément distribuées en des coordonnées cartésiennes normalement distribuées.
• La forme « polaire » transforme des coordonnées cartésiennes uniformément distribuées dans le cercle unité (obtenues par rejet) en des coordonnées normalement distribuées.

On peut également utiliser la méthode de la transformée inverse pour générer des nombres normalement distribués ; la méthode de Box-Muller est plus précise et plus rapide. On peut également envisager la méthode ziggourat, qui est beaucoup plus rapide.

La méthode polaire est celle utilisée par la bibliothèque standard du C++ du compilateur GCC pour échantillonner des variables de distribution normale.

Écritures

Transformation de Box-Muller

Soient $U_{1}$ et $U_{2}$ deux variables aléatoires indépendantes uniformément distribuées dans ]0,1].

Soient

$Z_{0}=R\cos(\Theta )={\sqrt {-2\ln U_{1}}}\cos(2\pi U_{2})\,$

et

$Z_{1}=R\sin(\Theta )={\sqrt {-2\ln U_{1}}}\sin(2\pi U_{2}).\,$

Alors Z₀ et Z₁ sont des variables aléatoires indépendantes suivant une loi normale centrée réduite.

Méthode polaire

Cette méthode, due à George Marsaglia (en) et T.A. Bray, est basée sur le fait suivant : si $(X,Y)$ est un point choisi uniformément sur le disque unité, alors $U=X^{2}+Y^{2}$ est une variable uniforme sur le segment $[0,1]$, et ${\textstyle ({\frac {X}{\sqrt {U}}},{\frac {Y}{\sqrt {U}}})}$ un point uniforme sur le cercle, tous deux indépendants. Il en résulte, par la transformée de Box-Muller, que

$Z_{0}=X\cdot {\sqrt {\frac {-2\ln U}{U}}},\quad Z_{1}=Y\cdot {\sqrt {\frac {-2\ln U}{U}}}$

sont des variables aléatoires indépendantes suivant une loi normale centrée réduite.

Le couple $(X,Y)$ est échantillonné par la méthode du rejet. Les variables $X$ et $Y$ sont tirées uniformément et indépendamment sur le segment $[-1,1]$. On calcule ensuite $U=X^{2}+Y^{2}$. Si $U\geq 1$ ou $U=0$ , rejetons-le et choisissons à nouveau un couple $(X,Y)$, jusqu'à ce que $U$ appartienne à $]0,1[$.

Explications

La justification de cette transformation vient de la transformation de la mesure de probabilités de la loi normale en coordonnées polaires :

${\frac {1}{{\sqrt {2\pi }}^{2}}}\mathrm {e} ^{-{\frac {x^{2}+y^{2}}{2}}}\,\mathrm {d} x\,\mathrm {d} y={\frac {1}{2\pi }}\mathrm {e} ^{-{\frac {r^{2}}{2}}}r\,\mathrm {d} r\,\mathrm {d} \theta =\left({\frac {1}{2}}\mathrm {e} ^{-{\frac {s}{2}}}\mathrm {d} s\right)\left({\frac {1}{2\pi }}\mathrm {d} \theta \right)$

en posant s = r².

On voit ainsi que les variables S et Θ sont indépendantes (la densité du couple est le produit des densités) et suivent deux lois distinctes :

• $S\sim {\mathcal {E}}\left({\frac {1}{2}}\right)$ : S suit une loi exponentielle de paramètre 1/2.
• $\Theta \sim {\mathcal {U}}\left(\left[0;2\pi \right]\right)$ : Θ suit une loi uniforme continue sur $\left[0;2\pi \right]$.

La variable S est alors générée par la méthode de la transformée inverse. Il suffit ensuite d'écrire les égalités $x=r\cos \theta$ et $y=r\sin \theta$.

Comparaison entre les deux formes

La méthode polaire est une méthode d'échantillonnage à rejet, qui n'utilise qu'une partie des nombres générés par la source aléatoire, mais elle est en pratique plus rapide que la transformation de Box-Muller car elle est plus simple à calculer :

• elle n'utilise pas de fonction trigonométrique, coûteuses en temps de calcul ;
• la génération de nombres aléatoires uniformes est plutôt rapide, il n'est donc pas gênant d'en gaspiller une partie. En moyenne, la part de points rejetés est (1 – π/4) ≈ 21,46 %. On génère donc en moyenne 4/π ≈ 1,2732 nombres aléatoires uniformes pour obtenir chaque nombre aléatoire normal.