Isolateur (optique)

Symbole d'un isolateur optique

Un isolateur optique de laboratoire

Un isolateur optique ou diode optique est un composant optique permettant la propagation de la lumière en sens unique. Ce type de composants est généralement utilisé pour éliminer les réflexions parasites dans un oscillateur paramétrique optique, tel qu'une cavité laser. Les isolateurs optiques utilisent l'effet Faraday (lequel fait tourner la polarisation par un effet magnéto-optique), et plus précisément le composant destiné à cet effet : le rotateur de Faraday.

Principe général

Rotateur de Faraday

Le composant principal d'un isolateur optique est le rotateur de Faraday. Le champ magnétique $B$ appliqué au rotateur de Faraday implique une rotation de la polarisation due à l'effet Faraday. L'angle de rotation, $\beta$ est donné par la relation:

$\beta =\nu Bd\,$

avec $\nu$, la Constante de Verdet du matériau et $d$ la longueur du rotateur. Le matériau peut être amorphe ou cristallin, solide, liquide ou gazeux. Pour le cas particulier des isolateurs, le rotateur est choisi de manière que l'angle soit de 45 degrés.

Il a été prouvé que la non-réciprocité est un critère déterminant pour les performances d'un isolateur optique.

Principe de l'isolateur

Effet d'un champ magnétique sur un dipôle électrique.

Les mécanismes physiques qui interviennent dans un isolateur optique peuvent être expliqués de manière imagée avec le modèle (simpliste) de l'électron élastiquement lié.

Une onde électromagnétique entrant dans un cristal vient exciter les atomes qui se mettent à osciller sous forme de dipôles induits. Dans le modèle de l'électron élastiquement lié, le noyau, très lourd, reste immobile tandis que l'électron oscille autour d'une position d'équilibre, comme s'il était maintenu au noyau par un ressort. Le dipôle est excité par le champ électrique de l'onde lumineuse, l'électron est soumis à la force de Lorentz:

$\mathbf {F} _{L}=-e\mathbf {E}$

(Avec $e$ la charge élémentaire de l'électron et $\mathbf {E}$ le vecteur champ électrique de l'onde)

Enfin, les dipôles rayonnent et réémettent une onde dont la polarisation est identique à leur axe d'oscillation: ici, la polarisation est identique à celle de l'onde qui les a créés.

Lorsqu'on introduit dans le matériau un champ magnétique, la force de Lorentz que subit le dipôle se voit ajouter un terme qui dépend du champ magnétique.

$\mathbf {F} _{L}=-e(\mathbf {E} -\mathbf {v} \times \mathbf {B} )$

(Avec $\mathbf {B}$ le vecteur champ magnétique appliqué au matériau et $\mathbf {v}$ la vitesse de l'électron)

L'électron n'oscille plus parallèlement au champ électrique mais avec un angle qui dépend entre autres de l'amplitude du champ magnétique. L'onde réémise par rayonnement des dipôles induits est, elle, polarisée selon l'axe d'oscillation des dipôles: la polarisation a tourné d'un angle (par exemple, $\alpha$).

Admettons maintenant qu'une onde entre dans le cristal, mais dans le sens opposé aux propagations précédentes. L'orientation du champ magnétique, elle, n'a pas changé. La polarisation du faisceau est de nouveau tournée d'un angle $\alpha$: elle ne revient pas à la polarisation initiale, mais on a désormais $2\alpha$. Le composant n'est donc pas réciproque.

Si $\alpha$ vaut 45°, le faisceau qui revient en sens inverse ressort polarisé à 90°. Il suffit d'introduire un polariseur en entrée pour éteindre totalement cette polarisation.

Isolateur dépendant de la polarisation

Généralités

Figure 2: Rotateur de Faraday avec polariseur et analyseur

Un isolateur dépendant de la polarisation (ou isolateur de Faraday) s'organise autour de trois parties : un polariseur d'entrée (polarisé linéaire vertical), un rotateur de Faraday et un polariseur de sortie (analyseur) polarisé à 45°. La lumière qui traverse l'isolateur en sens direct devient polarisée verticalement par le premier polariseur, tourne de 45° avec le rotateur de Faraday et est intégralement transmise par l'analyseur. En revanche, la lumière entrant en sens inverse est polarisée à 45° par le polariseur de sortie et tourne également de 45° avec le rotateur de Faraday. Cela la rend donc polarisée orthogonalement au polariseur d'entrée, elle est donc totalement absorbée.

La figure 2 illustre un rotateur de Faraday avec un polariseur d'entrée et un analyseur. Pour un isolateur dépendant de la polarisation, l'angle entre le polariseur et l'analyseur, $\beta$, doit être de 45° pour garantir l'isolation.

Les isolateurs dépendants de la polarisation sont couramment utilisés pour de l'optique en espace libre (non fibrée). En effet, la propagation dans l'air ne dégrade pas la polarisation, on a donc des systèmes à maintien de polarisation. Dans le cadre de l'optique fibrée, la direction de la polarisation est dispersée si les fibres ne sont pas à maintien de polarisation. En conséquence, l'angle formé entre le polariseur d'entrée et la polarisation du faisceau entrant mènera à une perte de puissance.

Lorsqu'on travaille à haute puissance, le polariseur d'entrée peut être avantageusement remplacé par un cube à séparation de polarisation. Le faisceau contrapropageant n'est ainsi plus absorbé mais réfléchi par l'isolateur, ce qui permet d'éviter l'échauffement du système.

Sensibilité à la longueur d'onde: Isolateurs accordables

Schéma de principe d'un isolateur optique

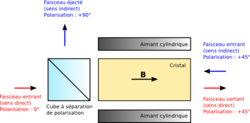
La constante de Verdet dépend de la longueur d'onde. Ceci limite en théorie les performances des isolateurs pour les sources à large bande spectrale. D'autre part, puisqu'il est nécessaire d'avoir une polarisation à 45° pour assurer une bonne isolation, un des paramètres du système doit être modifié pour avoir un isolateur accordable. En général, le champ magnétique est fourni par un puissant aimant cylindrique dans lequel est logé le cristal. Puisque l'effet Faraday dépend directement du champ magnétique, l'aimant peut-être translaté de manière à encercler plus ou moins le cristal. Les isolateurs ayant généralement une structure cylindrique, le réglage s'effectue le plus souvent avec une vis dans l'axe de propagation du faisceau.

En pratique, les isolateurs accordables peuvent être utilisés pour couvrir de larges bandes spectrales. Il est possible d'isoler des signaux sur des bandes de plus de 200 nm de large. La bande passante n’est dans ce cas limitée que par les traitements anti-reflets des composants. Cela requiert néanmoins d’avoir un rotateur de Faraday au milieu de la bande spectrale et avec une constante de Verdet faiblement dépendante de la longueur d’onde.

Isolateur indépendant de la polarisation

Figure 3: Schéma de principe d'un isolateur indépendant de la polarisation. En pratique, des collimateurs sont placés entre les fibres et le composant pour assurer un bon couplage.

Les isolateurs indépendants de la polarisation sont également faits en trois parties : une cale biréfringente (ayant sa direction de polarisation ordinaire verticale et la direction extraordinaire horizontale), un rotateur de Faraday et une cale biréfringente de sortie ayant sa direction de polarisation ordinaire à 45° et extraordinaire à -45°.

La lumière traversant en sens direct le système est divisée par la cale biréfringente en une composante verticale (0°) et une composante horizontale (90°), respectivement appelées rayon ordinaire (noté o) et rayon extraordinaire (noté e). Le rotateur de Faraday fait tourner chacun des deux rayons d'un angle de 45°. Le rayon o est alors à +45° et le e à -45°. Le cristal biréfringent de sortie recombine les deux composantes.

D'autre part, la lumière entrant en sens inverse dans l'isolateur est séparée en deux composantes, une ordinaire à 45° et une extraordinaire à -45°. Le rotateur de Faraday les fait tourner d'un angle de 45°, ce qui a pour effet de les incliner à 90° pour la composant ordinaire et 0° pour l'extraordinaire. Au lieu d'être recombinés à la sortie de la seconde cale biréfringente, les deux rayons divergent.

En général, des collimateurs sont utilisés à chaque extrémité de l'isolateur. En sens direct, le faisceau est divisé, recombiné, puis focalisé sur le collimateur de sortie. Dans le sens contraire, les rayons divergent et il n'y a donc pas de focalisation.

La figure 3 illustre la propagation de la lumière au travers d'un isolateur indépendant de la polarisation. Le passage en sens direct correspond au schéma du haut, le passage en sens inverse est représenté par celui du bas.

Les polarisateurs indépendants de la polarisation ne sont en général pas à maintien de polarisation. Ils introduisent un déphasage qui dépend à la fois de la longueur d'onde et de la température, ce qui conduit à une dépolarisation du signal.

Isolateurs fibrés

Les isolateurs fibrés sont fréquemment utilisés en laboratoire. Les polariseurs d'entrée et de sortie sont généralement des prismes biréfringents. Un des matériaux utilisés pour ces prismes peut-être le dioxyde de titane.

Lorsque les isolateurs sont fibrés, n’importe quelle polarisation peut entrer dans l’isolateur dans le sens opposé au sens passant. La sélection se fait lors du couplage entre la sortie de l’isolateur et la fibre de sortie: les faisceaux sont spatialement décalés de manière à ne pas pouvoir être couplés dans la fibre. Les isolateurs fibrés ont l’avantage d’être très compacts.

Il est possible de fabriquer des fibres optiques avec des constantes de Verdet élevées, ce qui permet d’envisager de faire des isolateurs de Faraday intrinsèques à la fibre, et plus seulement connectable à une fibre. En clair, il est envisageable de construire des fibres nativement à sens unique. Encore au stade de recherche, ces fibres pourraient être utiles pour les sources laser fibrées.

Isolateurs optiques et thermodynamique

En autorisant la lumière à aller d'un point froid vers un point chaud et en bloquant la propagation dans le sens inverse, les isolateurs optiques peuvent être compris comme en contradiction avec la loi de Kirchhoff et le second principe de la thermodynamique. Néanmoins, ce n'est pas le cas parce que l'isolateur doit absorber (et pas réfléchir) la lumière depuis le point chaud et pourra éventuellement la rayonner de nouveau vers le point le plus froid : bloquer le passage du point chaud vers le point froid n'empêche pas la création d'un nouveau chemin des photons entre ce point chaud et le point froid.

Critères de performances

Gain d’insertion

Avoir de faibles pertes en transmission est très important dans de nombreuses applications. Ces pertes sont déterminées à la fois par la qualité des polariseurs, les réflexions à chacune des surfaces traversées (et donc, la qualité des traitements anti-reflet) et la précision angulaire du rotateur.

Isolation

Le critère de performances principal d’un isolateur optique est son degré d’isolation, c’est-à-dire sa capacité à éliminer les rayons qui se propagent dans le mauvais sens. Les rotateurs de Faraday standard atteignent entre 30 et 40 dB d’isolation, mais les performances diminuent pour les composants à haute puissance. Pour diminuer l’éclairement, ils offrent une plus grande surface de cristal au faisceau. Cela rend cependant le signal plus sensible aux inhomogénéités du champ magnétique et diminue l’isolation. L’isolation peut également être dégradée si les polariseurs sont mal alignés ou si le faisceau n’est pas bien collimaté.

Pour pallier les éventuelles diminutions de performances en terme d’isolation, il est possible de monter l’un derrière l’autre deux isolateurs. Cela augmente les pertes d’insertion mais permet d’atteindre de bonnes performances en terme d’isolation, si bien qu’il est possible de trouver des isolateurs doublés dans le commerce.

Choix du cristal

L'élément le plus important d'un isolateur est le cristal dans lequel a lieu l'effet Faraday (le rotateur de Faraday) avec les caractéristiques qui font sa performance : une grande constante de Verdet, une faible absorption, un indice de réfraction non linéaire faible et un haut seuil d'endommagement. De plus, pour éviter les effets thermiques (lentille thermique notamment), le cristal doit être le plus court possible. En général, ces conditions font choisir du terbium dopé borosilicate ou du terbium-gallium (TGG) pour une plage de longueur d'onde entre 700 et 1100 nm, ou encore du YIG pour les fibres utilisées dans les télécommunications (généralement entre 1310 et 1550 nm). Les isolateurs au YIG commerciaux atteignent des isolations supérieures à 30 dB.

Les isolateurs optiques diffèrent des isolateurs à lames quart d'onde en ce que le rotateur de Faraday provoque un effet non réciproque tout en maintenant une polarisation rectiligne. En fait, le rotateur de Faraday fait tourner la polarisation toujours dans le même sens, indépendamment du sens de propagation de l'onde.

Applications

• Les isolateurs peuvent servir à protéger les sources laser ou amplificateurs de la lumière réfléchie. Lorsqu’on met en chaîne des amplificateurs, il peut être également judicieux de placer des isolateurs pour éviter l’amplification de photons spontanés. Dans le domaine des télécommunications, l’amplification régulière du signal est nécessaire et les amplificateurs sont également entourés d’isolateurs.

• Les propriétés de polarisation des isolateurs peuvent être utilisées dans les résonateurs pour forcer la polarisation linéaire ou faire du verrouillage de phase avec rotation non-linéaire de polarisation.

• 
  Isolateur permettant de protéger une source laser à 780 nm.
• 
  Isolateur placé derrière un Amplificateur optique.

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « optical isolator » (voir la liste des auteurs).

Articles connexes

• Fibre optique
• Coupleur (optique)
• Circulateur (optique)
• Isolateur pour guide d'ondes

Liens externes

• Isolateurs pour les télécommunications, belles images