Entrelacs et graphes

La théorie des nœuds et la théorie des graphes ont des rapports entre elles. Un entrelacs d'apparence compliquée peut être codé par un graphe planaire.
Diagramme d'un nœud ou d'un entrelacs[modifier | modifier le code]

Un nœud ou entrelacs dans l'espace peut être projeté sur le plan euclidien ; on obtient un diagramme de ce nœud ou entrelacs si cette projection est génériquement régulière, c'est-à-dire injective presque partout, à l'exception d'un nombre fini de points de croisements simples où la projection envoie seulement 2 points de l'entrelacs sur le même point. De plus, les directions des brins à ces deux points doivent être distinctes. Enfin on doit indiquer quel brin est dessus et lequel est dessous en interrompant le tracé ou par un codage. Un tel diagramme caractérise la classe d'isotopie de l'entrelacs.
En termes de théorie des graphes, un diagramme de nœud ou d'entrelacs est simplement un graphe planaire dont tous les sommets sont de degré 4, ces sommets étant labellisés par l'information des dessus-dessous.
Graphe associé à un nœud ou un entrelacs[modifier | modifier le code]




Une construction associée à un diagramme d'entrelacs facilite la manipulation de celui-ci. En effet, la projection précédente décompose le plan en plusieurs composantes connexes : le diagramme lui-même, de dimension 1, et une zone non bornée et des composantes homéomorphes à des disques, de dimension 2.
On peut alors attacher une couleur grise ou blanche à chacune de ces zones de la manière suivante : colorez en gris la zone non bornée et, pour chaque croisement, colorez en gris la zone opposée au croisement. Le théorème de Jordan permet d'affirmer que ce processus est bien défini [1].
Définissez ensuite un graphe planaire dont les sommets sont au "centre" de chaque zone blanche, et dont les arêtes passent par chaque croisement, entre les deux brins de l'entrelacs. L'information du dessus-dessous est codée par un signe + ou - étiquetant chaque arête. L'arête est étiquetée + si le brin venant de la gauche passe au-dessus, et étiquetée - sinon.
On peut représenter ce signe par la convention d'un trait plein pour un signe + et d'un trait en pointillé pour le signe -. Il y a un choix global des signes, un changement de ce choix correspond à la réflexion dans un miroir. Lorsque le nœud ou l'entrelacs est alterné (alternance des passages dessus-dessous), toutes les arêtes ont le même signe.
Le diagramme de nœud est alors le graphe médial du graphe que nous venons de définir.

Passage inverse, du graphe à l'entrelacs[modifier | modifier le code]
L'animation ci-dessous montre comment procéder pour passer du graphe à l'entrelacs.
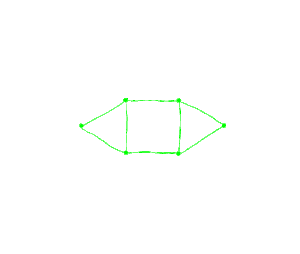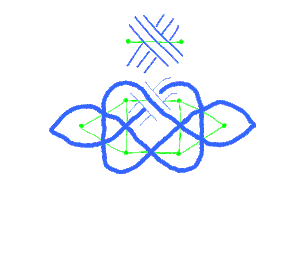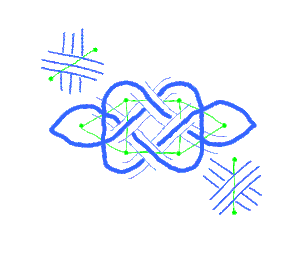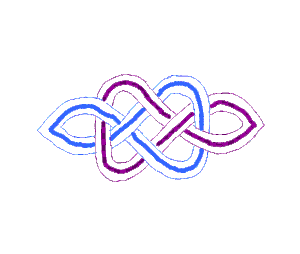
Cette correspondance entre diagrammes d'entrelacs et graphes plantaires permet de dessiner de beaux entrelacs, pour les coder d'une manière plus aisée à manipuler, ou pour les déformer, les comparer ou les mémoriser.

Mouvements de Reidemeister[modifier | modifier le code]
Les mouvements de Reidemeister sont des modifications locales du diagramme d'entrelacs qui préservent la classe d'isotopie et permettent de passer de n'importe quel diagramme à n'importe quel autre. Ces mouvements se transcrivent sur le graphe associé comme indiqué dans les figures ci-dessous.
-
Type I : suppression/ajout d'une boucle ou d'une arête libre
-
Type II : suppression/ajout d'une arête double de signes contraires
-
Type III (et son image miroir)
Comme pour les diagrammes, deux graphes planaires à arêtes signées sont associés au même entrelacs si et seulement si on peut passer de l'un à l'autre par une série de mouvements de Reidemeister.
Voir aussi[modifier | modifier le code]
- Code de Gauss d'un entrelacs.
- Enlacement de deux courbes.
Notes et références[modifier | modifier le code]
- Alexeï Sossinsky, Nœuds, Paris, Seuil, , p. 59 à 70
- (en) Peter Cromwell, Knots And Links, Cambridge University Press, , p. 51 à 56
- (en) Bela Bollobas, Modern Graph Theory, Springer, , p. 368 à 370
- (en) Colin C. Adams, The Knot Book, American Mathematical Society, 1994, 2001, 2004 (lire en ligne), p. 51 - 55
Liens externes[modifier | modifier le code]
- (fr + en + de) Tutoriel sur les entrelacs
- (en) « Biquasiles and Dual Graph Diagrams »
- Page mathcurve sur le sujet
- Des beaux entrelacs sur Images des maths
- [vidéo] VideoDiMath, Dessiner de beaux entrelacs (Christian Mercat) sur YouTube, (consulté le )




