Diffusion dynamique de la lumière
La diffusion dynamique de la lumière (en anglais, dynamic light scattering ou DLS) est une technique d'analyse spectroscopique non destructive permettant d'accéder à la taille de particules en suspension dans un liquide ou de chaînes de polymère en solution de 1 à 500 nm[réf. nécessaire] de diamètre environ.
Principe[modifier | modifier le code]
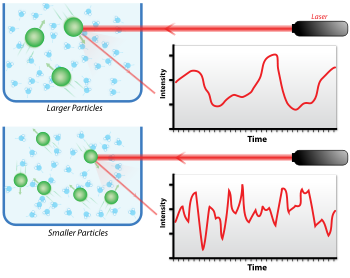
Lorsque la lumière d'un laser atteint des petites particules dans une microcuvette, la lumière diffuse dans toutes les directions. Ce phénomène est principalement de la diffusion de Rayleigh, diffusion élastique où les particules sont plus petites que la longueur d'onde considérée. On peut mesurer l'intensité de la lumière diffusée par les particules à un angle considéré (90° typiquement) au cours du temps. Cette dépendance en temps vient du fait que les particules dans un liquide sont soumises au mouvement brownien à cause de l'agitation thermique. La distance entre diffuseurs (concentration locale) change ainsi sans cesse. Il en résulte des interférences constructives ou destructives et l'intensité totale mesurée contient des informations sur la vitesse de mouvement des particules.
Traitement mathématique[modifier | modifier le code]
Un traitement mathématique est mis en œuvre. On définit la fonction d'autocorrélation qui permet de comparer le signal mesuré à lui-même, mais avec un petit décalage temporel. Une modélisation graphique permet d'extraire un temps caractéristique de décroissance de cette fonction. Si l'autocorrélation décroît rapidement (taux faible), c'est que le signal mesuré varie rapidement. C'est le cas lorsque les particules se déplacent assez vite, donc qu'elles sont de petites tailles (plus mobiles). L'inverse de ce temps caractéristique (dit temps de relaxation) est lié au coefficient de diffusion des particules par la relation suivante: avec D le coefficient de diffusion, q le vecteur d'onde et le temps de relaxation. L'équation de Stokes-Einstein permet alors d'obtenir le rayon hydrodynamique des particules: où désigne la constante de Boltzmann et la viscosité du fluide.
Résultats obtenus[modifier | modifier le code]
Le rayon hydrodynamique est le rayon d'une sphère théorique qui aurait le même coefficient de diffusion que la particule considérée. Dans le cas d'une pelote polymère, ce rayon correspond au rayon d'une sphère dans laquelle le solvant ne pénètre pas. Pour une particule chargée la sphère considérée contient la particule entourée de sa couche diffuse, ce qui entraine une surestimation par rapport à une mesure de taille par microscopie.
En réalité il existe une dispersité des tailles rencontrées et différentes méthodes sont mises en œuvre pour extraire l'intensité diffusée des différentes populations. Les différences sont très marquées en intensité et la présence d'impuretés ou d'agrégats sont très visibles même en très petit nombre.
On obtient donc un rayon hydrodynamique, un indice de polydispersité et des indices sur l'allure du profil de distribution des tailles de particules de l'échantillon, en nombre, volume ou intensité.







