Coefficient de pression

Le coefficient de pression est un coefficient aérodynamique adimensionnel facilitant l’étude et la représentation graphique de la distribution des pressions autour de corps placés dans un écoulement de fluide.

Définition

Le coefficient de pression $C_{p}$ est un coefficient aérodynamique adimensionnel de pression facilitant l’étude et la représentation graphique de la distribution des pressions autour de corps placés dans un écoulement de fluide.

Dans l’air, ou tout autre fluide dont la masse volumique est suffisamment faible, il s'écrit :

$C_{p}={p-p_{\infty } \over {\frac {1}{2}}\rho _{\infty }v_{\infty }^{2}}$

où :

p est la pression statique mesurée au point considéré,

$p_{\infty }$ la pression statique de l’écoulement (c.-à-d. à l’écart des perturbations créées par le corps),

$v_{\infty }$ la vitesse de l’écoulement loin du corps,

$\rho _{\infty }$ la masse volumique du fluide (l’air, par exemple).

Les coefficients de pression sont utilisés, dans tous les travaux de mécanique des fluides, depuis les écoulements incompressibles jusqu’aux écoulements hypersoniques.

Dans certain cas, la pression du vent sur un corps peut être visible, comme, par exemple, la pression du vent autour du point d’arrêt de ce ballon censé être sphérique.

Dans un écoulement incompressible, le $C_{p}$ au point d’arrêt (ou aux points d’arrêt lorsqu’il y en a plusieurs) vaut toujours 1 et c’est la plus forte valeur existant dans l’écoulement ; au culot des corps, même profilés, existe une zone où le coefficient de pression est négatif, mais en beaucoup d'autres endroits d'un écoulement les $C_{p}$ sont négatifs.

Écoulements incompressibles et courbe de distribution des pressions

L’équation de Bernoulli (qui est valide en dehors de la couche limite sur les corps) permet de lier mathématiquement les coefficients de pression $C_{p}$ mesurés localement autour d’un corps à des coefficients de vitesse $C_{v}$ qui représentent la vitesse locale du fluide au-dessus de sa couche limite. NdBP : Par chance, la pression statique au-dessus de la couche limite se transmet jusqu’à la surface du corps où elle peut être mesurée à l’aide de petits orifices.

Les libellés des $C_{p}$ et $C_{v}$ naissent naturellement de l’équation de Bernoulli pour les gaz lorsqu’on applique celle-ci à deux points de la même ligne de courant, le deuxième de ces points étant pris loin du corps (à l’infini amont, par exemple) :

${\frac {1}{2}}\rho v^{2}+p={\frac {1}{2}}\rho v_{\infty }^{2}+p_{\infty }$

En recombinant différemment cette égalité on peut écrire :

$p-p_{\infty }={\frac {1}{2}}\rho v_{\infty }^{2}-{\frac {1}{2}}\rho v^{2}$

En divisant les deux membres de l’égalité par la pression dynamique ${\frac {1}{2}}\rho v_{\infty }^{2}$ on obtient finalement :

${p-p_{\infty } \over {\frac {1}{2}}\rho _{\infty }v_{\infty }^{2}}=1-{\frac {v^{2}}{v_{\infty }^{2}}}$

On reconnaît $C_{p}$ dans le premier membre de cette égalité. Si l’on définit à présent le deuxième terme du deuxième membre comme le carré d’un coefficient de vitesse $C_{v}$ :

$C_{v}={\frac {v}{v_{\infty }}}$

On obtient :

$C_{p}=1-C_{v}^{2}$

Cette égalité très simple constitue la variante adimensionnelle de l’équation de Bernoulli. Elle n'est valide qu'en dehors de la couche limite pour les écoulements stationnaires incompressibles.

Contrairement à ce que leur libellé peut laisser penser, ces coefficients adimensionnels de pression et de vitesse $C_{p}$ et $C_{v}$ sont extrêmement intuitifs et représentent bien les pressions et les vitesses qui intéressent les Mécaniciens des Fluides ; ceci explique pourquoi ils apparaissent dans tous les rapports d’essais en souffleries.

Trois représentations du $C_{p}$ autour de la sphère et du Tube de Pitot.

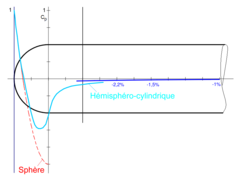
L’image ci-contre montre trois présentations possibles du coefficient de pression autour de la sphère isolée et d’un corps hémisphéro-cylindrique tel que le tube de Pitot (ou Antenne de Prandtl), ce coefficient de pression étant calculé ici théoriquement (en non visqueux, c-à-d sans couche limite).

La première image de la galerie ci-dessous reprend la distribution théorique des $C_{p}$ sur la sphère, mais en y ajoutant les $C_{p}$ réellement mesurés en sous-critique et en super-critique. On note que la distribution réelle des $C_{p}$ est très différente de la distribution théorique, spécialement au premier régime (bas nombre de Reynolds).

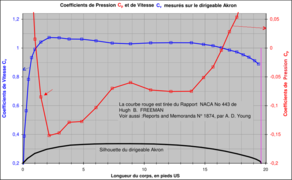
L'image suivante de la galerie fait apparaître visuellement la relation mathématique entre le coefficient de pression mesuré et le coefficient de vitesse autour d’un très grand modèle du dirigeable Akron à l’incidence nulle (ce modèle mesurait 6 m de longueur).

Ainsi pour ce corps profilé 3D, le coefficient de pression $C_{p}$ est, au point considéré, la surpression ou sous-pression relative de l’écoulement (relative à la pression dynamique). Ce $C_{p}$ varie depuis l’unité (au point d’arrêt du corps, par définition) à des valeurs rapidement négatives, pour finir à une valeur positive mais nettement inférieure à l’unité au culot du corps. Le coefficient de vitesse $C_{v}$ est, au point considéré, la vitesse relative de l’écoulement (relative à la vitesse de l’écoulement loin du corps). Ce $C_{v}$ varie de 0 au point d’arrêt (par définition) à une valeur au-dessus de l’unité en finissant par une valeur légèrement négative au culot du corps.

L'intégration des $C_{p}$ sur toute la surface du corps donne le $C_{x}$ de pression ; dans le cas d'un corps profilé, comme ici, ce $C_{x}$ de pression est très faible, ce qui signifie que le $C_{x}$ des corps profilés est principalement un $C_{x}$ de friction.

Si l'on observe ci-dessus la variante adimensionnelle de l'équation de Bernoulli, on constate que le coefficient de pression $C_{p}$ est lié linéairement au carré du coefficient de vitesse $C_{v}$, c'est ce qui explique que dans le rapport NACA n^o 824 (réf. ci-dessous), ce soit le carré du $C_{v}$ qui est utilisé pour représenter la pression. L'image suivante de la galerie montre la distribution des pressions dans le plan de symétrie d'une berline routière. On observe qu'il existe sur l'avant du capot moteur et sur le haut du parebrise deux zones dépressionnaires (c.-à-d. que les pressions sur ces deux zones tendent à tirer le véhicule en avant).

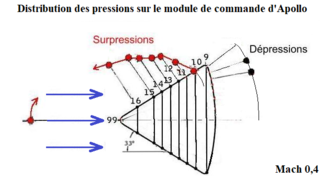
La dernière image de la galerie montre les coefficients de pression relevés sur le cône de la capsule Apollo (sans sa tour de sauvetage) ainsi que sur son bouclier thermique. Au franchissement des épaules de ce cône, les $C_{p}$ deviennent évidemment négatifs puisque l'écoulement, en cet endroit, est en survitesse (survitesse par rapport à la vitesse de l'écoulement loin du corps).

• 
  Distribution des pressions (Cp) sur la sphère d'après Achenbach.
• 
  Distribution des pressions sur le cylindre infini présenté en travers d'un écoulement.
• 
  Distribution des $C_{p}$ et $C_{v}$ autour du dirigeable Akron.
• 
  Distribution des $C_{p}$ dans le plan de symétrie d'un berline routière DrivAer Fastback.
• 
  Distribution des $C_{p}$ sur le flanc d'un fuselage d'avion.
• 
  Distribution des pressions sur le cône d'Apollo (module de commande) à l'incidence zéro.
• 
  Distribution des pressions sur la torpille Mk 25

Exemples d'utilisation de la courbe de distribution des pressions

Sur les véhicules thermiques à moteur avant, les ouvertures permettant le refroidissement du moteur sont évidemment placées près du point d'arrêt (où le $C_{p}$ vaut $1$, image ci-dessus).

Distribution des pressions sur le poisson tassergal (ou bluefish) d'après DuBois et coll.

Les expérimentations ont révélé que les yeux des poissons sont placés très près du point avant de $C_{p}$ nul de la courbe de distribution des pressions à leur surface, de sorte qu'ils peuvent nager aux plus hautes vitesses sans que leurs globes oculaires soient distordus par la surpression ou la sous-pression due à la vitesse. De même, l'ouverture de leurs ouïes est placée dans la zone de $C_{p}$ minimum afin d'activer la circulation d'eau à l'intérieur des ouïes et le cœur est placé dans la même zone afin d'accroître sa course d'expansion pendant la nage rapide

Autres exemples de distribution des pressions

• 
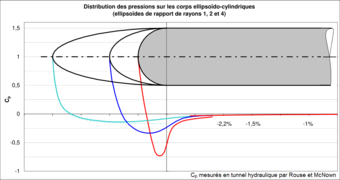
  Distribution des pressions sur trois corps ellipsoïdo-cylindriques.
• 
  Distribution des pressions sur le corps hémisphéro-cylindrique (tube de Pitot).
• 
  Distribution des pressions sur le cylindre à tête plate exposé axialement dans un écoulement.

Voir aussi

Bibliographie

• Sighard F. Hoerner (en), Résistance à l’avancement dans les fluides, Paris, Gauthier-Villars éditeurs, 1965
• A. Bonnet et J. Luneau, Aérodynamique, théories de la dynamique des fluides, Cépaduès-Éditions, 1989
• Th. Faure, Aérodynamique appliquée, 2006
• (en) John D. Anderson, Fundamentals of Aerodynamics, McGraw-Hill, 2011

Articles connexes

• Coefficient de vitesse
• Avant-corps (mécanique des fluides)

Liens externes

• Summary of Airfoil Data, Naca Report No. 824, by Ira H. Abbott, Albert E. von Doenhoff, and Louis S. Stivers Jr.