Système anastigmatique à trois miroirs
Un télescope anastigmatique à trois miroirs est un télescope anastigmatique construit avec trois miroirs courbes, permettant de minimiser les trois principales aberrations optiques – l'aberration sphérique, la coma et l'astigmatisme. Cette conception est principalement utilisée pour obtenir de larges champs de vue, beaucoup plus importants qu'avec des télescopes ayant seulement une ou deux surfaces courbes.
Un télescope ayant seulement un miroir courbe, tel qu'un télescope de Newton, aura toujours des aberrations. Si le miroir est sphérique, il souffrira d'aberration sphérique. Si le miroir est parabolique pour corriger l'aberration sphérique, alors il souffrira nécessairement de coma et d'astigmatisme hors-axe. Avec deux miroirs courbes, tels que dans un télescope Ritchey-Chrétien, la coma peut également être minimisée. Ceci permet d'avoir un plus large champ de vue, et l'astigmatisme résiduel est symétrique autour des objets distordus, permettant de faire de l'astrométrie sur l'ensemble du champ de vue. Cependant, l'astigmatisme peut être réduit en rajoutant un troisième élément optique courbe. Quand cet élément est un miroir, le résultat est un système anastigmatique à trois miroirs. En pratique, la conception peut comporter un nombre quelconque de miroirs de repliement plans, utilisés pour diriger le chemin optique dans des configurations plus compactes.
Histoire
[modifier | modifier le code]De nombreuses combinaisons de trois miroirs peuvent être utilisées pour annuler l'ensemble des aberrations du troisième ordre. En général, celles-ci nécessitent de résoudre un ensemble d'équations relativement compliquées. Cependant, quelques configurations sont néanmoins assez simples pour pouvoir être conçues à partir de quelques concepts intuitifs.
Télescope de Paul
[modifier | modifier le code]La première combinaison fut proposée en 1935 par Maurice Paul[1]. L'idée de base derrière la solution de Paul est que les miroirs sphériques, avec une obstruction d'ouverture au centre de courbure, ont seulement de l'aberration sphérique – pas de coma ni d'astigmatisme (mais ils produisent une image sur une surface courbe ayant un rayon égal à la moitié de celui du miroir sphérique). Donc si l'aberration sphérique peut être corrigée, un très large champ de vue peut être obtenu. Ceci est similaire à la conception de Schmidt conventionnelle, mais le télescope de Schmidt réalise cela avec une lame de correction réfractive au lieu d'un troisième miroir.
L'idée de Paul fut de partir d'un compresseur de faisceau de Mersenne, qui ressemble à un Cassegrain constitué de deux paraboloïdes confocaux, les deux faisceaux d'entrée et de sortie étant collimatés. Le faisceau d'entrée comprimé est alors dirigé vers un miroir tertiaire sphérique, ce qui produit une aberration sphérique traditionnelle. L'idée clé de Paul est que le secondaire peut être remplacé par un miroir sphérique.
Une façon d'examiner cela est d'imaginer que le miroir tertiaire, qui souffre d'aberration sphérique, est remplacé par un télescope de Schmidt, avec une lame de correction en son centre de courbure. Si les rayons de courbure du secondaire et du tertiaire sont identiques, mais de signes opposés, et si le centre de courbure du tertiaire est placé directement au vertex du miroir secondaire, alors la lame de Schmidt serait placée sur le dessus du miroir secondaire parabolique. Par conséquent, la lame de Schmidt nécessaire pour rendre le miroir tertiaire équivalent à un télescope de Schmidt est éliminée par le paraboloïde représenté par le secondaire convexe du système de Mersenne, car chacun corrige la même quantité d'aberration sphérique, mais de signe opposé. Par ailleurs, comme le système de Mersenne + Schmidt est la somme de deux systèmes anastigmatiques (le système de Mersenne est anastigmatique comme le système de Schmidt), le système résultant est également anastigmatique, du fait que les aberrations de 3ème ordre sont additives[2]. De plus, le secondaire est désormais plus facile à fabriquer. Cette conception est également appelée Mersenne–Schmidt, puisqu'elle utilise une configuration de Mersenne comme correcteur d'un télescope de Schmidt.
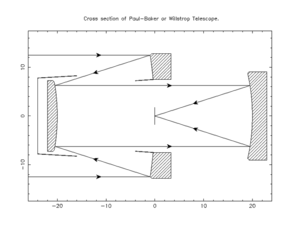
Télescope Paul–Baker
[modifier | modifier le code]La solution proposée par Paul avait un plan focal courbe, mais cela fut corrigé dans la conception Paul–Baker, introduite en 1969 par James Gilbert Baker (en)[3]. La conception Paul–Baker augmente l'espacement entre les miroirs secondaire et tertiaire et transforme le miroir secondaire sphérique en miroir elliptique, ce qui corrige la courbure de champ et aplatit le plan focal[4].
Télescope Korsch
[modifier | modifier le code]Un ensemble plus général de solutions fut développé par Dietrich Korsch en 1972[5]. Un télescope Korsch est corrigé de l'aberration sphérique, de la coma, de l'astigmatisme et de la courbure de champ et peut avoir un large champ de vue tout en ayant peu de lumière parasite dans le plan focal.
Exemples
[modifier | modifier le code]- Le télescope spatial James Webb est un système anastigmatique à trois miroirs.
- Le télescope spatial Euclid utilisera un télescope Korsch.
- Le projet « Cambridge University Three-Mirror Telescope » comprend un modèle fonctionnel de 100 mm construit en 1985 et un prototype de 500 mm construit en 1986.
- Le télescope de l'observatoire Vera-C.-Rubin (anciennement appelé Large Synoptic Survey Telescope) est un système anastigmatique à trois miroirs modifié de type Paul–Baker.
- Les télescopes KH-11 Kennen (ou peut-être ceux du projet abandonné Future Imagery Architecture) pourraient être de type anastigmatique à trois miroirs, puisque les télescopes inutilisés donnés à la NASA par la National Reconnaissance Office sont de ce type.
- Le Télescope géant européen sera de type anastigmatique à trois miroirs, avec deux miroirs plans supplémentaires de repliement.
- Les satellites d'observation de la Terre Deimos‑2 et DubaiSat‑2 utilisent tous deux un télescope Korsch anastigmatique à trois miroirs[6],[7].
- Le spectromètre imageur Ralph sur la sonde New Horizons.
- WFIRST utilise un système anastigmatique à trois miroirs hors axe[8].
Références
[modifier | modifier le code]- Maurice Paul, « Systèmes correcteurs pour réflecteurs astronomiques », Revue d'Optique Théorique et Instrumentale, vol. 14, no 5, , p. 169–202
- (en) R. N. Wilson, Reflecting Telescope Optics I, Springer, (ISBN 978-3-540-40106-3), p. 227
- (en) J.G. Baker, « On improving the effectiveness of large telescopes », IEEE Transactions on Aerospace and Electronic Systems, vol. AES-5, no 2, , p. 261–272 (DOI 10.1109/TAES.1969.309914, Bibcode 1969ITAES...5..261B)
- (en) V. Sacek, « Paul-Baker and other three-mirror anastigmatic aplanats », Telescope-Optics.net, (consulté le )
- (en) Dietrich Korsch, « Closed form solution for three-mirror telescopes, corrected for spherical aberration, coma, astigmatism, and field curvature », Applied Optics, vol. 11, no 12, , p. 2986–2987 (DOI 10.1364/AO.11.002986, Bibcode 1972ApOpt..11.2986K)
- (en) « DEIMOS‑2: Cost effective, Very-high Resolution Multispectral Imagery »
- « Technical Specifications of DubaiSat 2 »
- (en) D.A. Content, R. Goullioud, J.P. Lehan et J.E. Mentzell, « Optical design trade study for the Wide Field Infrared Survey Telescope [WFIRST] », Conference Proceedings of the SPIE, vol. 8146, (DOI 10.1117/12.898528, lire en ligne)
