Processus de décision markovien
En théorie de la décision et en théorie des probabilités, un processus de décision markovien (en anglais Markov decision process, MDP) est un modèle stochastique où un agent prend des décisions et où les résultats de ses actions sont aléatoires. Les MDPs sont utilisés pour étudier des problèmes d'optimisation à l'aide d'algorithmes de programmation dynamique ou d'apprentissage par renforcement. Les MDPs sont connus depuis les années 1950[1]. Une grande contribution provient du travail de Ronald A. Howard avec son livre de 1960, Dynamic Programming and Markov Processes. Ils sont utilisés dans de nombreuses disciplines, notamment la robotique, l'automatisation, l'économie et l'industrie manufacturière.
Un processus de décision markovien est un processus de contrôle stochastique discret. À chaque étape, le processus est dans un certain état et l'agent choisit une action . La probabilité que le processus arrive à l'état est déterminée par l'action choisie. Plus précisément, elle est décrite par la fonction de transition d'états . Donc, l'état dépend de l'état actuel et de l'action sélectionnée par le décideur. Cependant, pour un et un , le prochain état est indépendant des actions et états précédents. On dit alors que le processus satisfait la propriété de Markov.
Quand le processus passe de l'état à l'état avec l'action , l'agent gagne une récompense .
Les MDPs sont une extension des chaînes de Markov. La différence est l'addition des actions choisies par l'agent et des récompenses gagnées par l'agent. S'il n'y a qu'une seule action à tirer dans chaque état et que les récompenses sont égales, le processus de décision markovien est une chaîne de Markov.
Définition intuitive[modifier | modifier le code]
Afin de comprendre ce qu'est un MDP, supposons que l'on ait un système évoluant dans le temps comme un automate probabiliste. À chaque instant le système est dans un état donné et il existe une certaine probabilité pour que le système évolue vers tel ou tel autre état à l'instant suivant en effectuant une transition.
Supposons maintenant que l'on doive contrôler ce système boite noire de la meilleure façon possible. L'objectif est de l'amener dans un état considéré comme bénéfique, en évitant de lui faire traverser des états néfastes. Pour cela, on dispose d'un ensemble d'actions possibles sur le système. Pour compliquer la chose, on supposera que l'effet de ces actions sur le système est probabiliste : l'action entreprise peut avoir l'effet escompté ou un tout autre effet. L'efficacité du contrôle est mesurée relativement au gain ou à la pénalité reçue au long de l'expérience.
Ainsi, un raisonnement à base de MDP peut se ramener au discours suivant : étant dans tel cas et choisissant telle action, il y a tant de chance que je me retrouve dans tel nouveau cas avec tel gain.
Pour illustrer les MDP, on prend souvent des exemples issus de la robotique mobile (avec les positions pour états, les commandes comme actions, les mouvements comme transitions et l'accomplissement/échec de tâches comme gains/pénalités).
Hypothèse de Markov[modifier | modifier le code]
Dans les MDP, l'évolution du système est supposée correspondre à un processus markovien. Autrement dit, le système suit une succession d'états distincts dans le temps et ceci en fonction de probabilités de transitions. L'hypothèse de Markov consiste à dire que les probabilités de transitions ne dépendent que des n états précédents. En général, on se place à l'ordre n = 1, ce qui permet de ne considérer que l'état courant et l'état suivant.
Définition formelle[modifier | modifier le code]
Un MDP est un quadruplet définissant:
- un ensemble d'états , qui peut être fini, dénombrable ou continu; cet ensemble définit l'environnement tel que perçu par l'agent (dans le cas d'un robot, on peut voir cela comme l'ensemble produit des valeurs de ses différents capteurs);
- un ensemble d'actions , qui peut être fini, dénombrable ou continu et dans lequel l'agent choisit les interactions qu'il effectue avec l'environnement (dans le cas d'un robot on peut voir cela comme l'ensemble produit des paramètres de ses différentes commandes);
- une fonction de transition ; cette fonction définit l'effet des actions de l'agent sur l'environnement: représente la probabilité de se retrouver dans l'état en effectuant l'action , sachant que l'on était à l'instant d'avant dans l'état .
ainsi définie représente le cas le plus général; dans un environnement déterministe, on aura plutôt .
- une fonction de récompense ; elle définit la récompense (positive ou négative) reçue par l'agent: est la probabilité d'obtenir une récompense pour être passé de l'état à en ayant effectué l'action . Ici encore cette définition est très générale, bien souvent on se contentera par exemple des cas particuliers suivants :
- (récompense déterministe, c'est le choix que nous adopterons dans la suite) ;
- (récompense déterministe rattachée à l'action en ignorant son résultat) ;
- (récompense déterministe rattachée à un état donné).
Dans la littérature, la fonction de récompense est parfois remplacée par une fonction de coût[réf. nécessaire].
NB: nous ne considérons ici que les modèles dans lesquels le temps est discrétisé, c'est-à-dire que la «trajectoire» de l'agent dans l'environnement est décrite par une suite d'états (), et non par une fonction avec . De même on notera la suite des actions prises par l'agent. On pourra consulter [2] pour une description des MDP à temps continu.
Exemple de MDP[modifier | modifier le code]
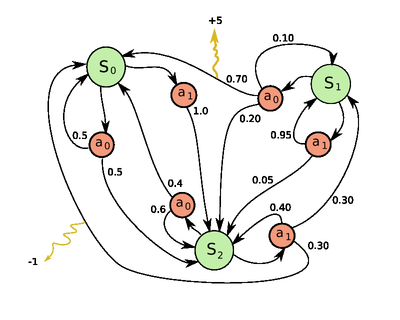
L'exemple donné ci-contre représente un processus de Décision Markovien à trois états distincts représentés en vert. Depuis chacun des états, on peut effectuer une action de l'ensemble . Les nœuds rouges représentent donc une décision possible (le choix d'une action dans un état donné). Les nombres indiqués sur les flèches sont les probabilités d'effectuer la transition à partir du nœud de décision. Enfin, les transitions peuvent générer des récompenses (dessinées ici en jaune).
- La matrice de transition associée à l'action est la suivante :
- La matrice de transition associée à l'action est la suivante :
En ce qui concerne les récompenses,
- on perçoit une récompense de +5 lorsque l'on passe de l'état à l'état en accomplissant l'action
- on perçoit une récompense de -1 (aussi appelée pénalité) lorsque l'on passe de l'état à l'état en accomplissant l'action
Remarques[modifier | modifier le code]
Le modèle MDP présenté ici est supposé stable dans le temps, c'est-à-dire que les composants du quadruplet sont supposés invariants. Il n'est donc pas applicable en l'état pour un système qui évolue, par exemple pour modéliser un système qui apprend contre un autre agent.
Politiques, fonctions de valeurs et équations de Bellman[modifier | modifier le code]
Politique[modifier | modifier le code]
Une politique décrit les choix des actions à jouer par l'agent dans chaque état. Formellement, il s'agit donc d'une fonction dans le cas d'une politique déterministe ou dans le cas stochastique. On note parfois la probabilité de jouer a dans l'état s, i.e. , la probabilité de jouer a à l'instant t sachant que l'état à l'instant t est s. Cette valeur est indépendante de t : on parle de politique stationnaire. Etant donné un MDP et une politique, on obtient une chaîne de Markov avec récompense. Nous nous plaçons dans le cas déterministe.
Critère[modifier | modifier le code]
L'agent choisit une politique à l'aide de la fonction de récompense . Notons la récompense effective obtenue après avoir effectué l'action par l'agent qui suit la politique . Voici plusieurs critères d'intérêts que l'agent peut chercher à maximiser :
- : espérance de la somme des récompenses à un horizon fini fixé ;
- ou : récompense moyenne à long terme ;
- : récompense escomptée (ou amortie) à horizon infini où .
Le dernier critère est courant et c'est celui que nous adoptons dans la suite. La valeur de permet de définir l'importance que l'on donne au futur. Quand nous sommes face à un agent «pessimiste» qui ne cherche qu'à optimiser son gain immédiat. À l'opposé si , l'agent est «optimiste» puisqu'il tient de plus en plus sérieusement compte du futur lointain (si , l'agent tient autant compte du futur lointain que du gain immédiat).
Fonctions de valeurs[modifier | modifier le code]
Lorsqu'une politique et un critère sont déterminés, deux fonctions centrales peuvent être définies :
- : c'est la fonction de valeur des états; représente le gain (selon le critère adopté) engrangé par l'agent s'il démarre à l'état et applique ensuite la politique ad infinitum.
- : c'est la fonction de valeur des états-actions; représente le gain engrangé par l'agent s'il démarre à l'état et commence par effectuer l'action , avant d'appliquer ensuite la politique ad infinitum.
Équation de Bellman[modifier | modifier le code]
Les deux fonctions sont intimement liées. On a toujours et, dans le cas du gain amorti à horizon infini, on peut également écrire que:
Cette dernière relation montre que la fonction vérifie une relation de récurrence appelée équation de Bellman:
L'équation de Bellman s'écrit comme l'équation linéaire suivante dans la chaîne de Markov avec récompenses "applatie" à partir du processus de décision markovien et la politique :
où est le vecteur contenant les valeurs pour chaque état, est la matrice des récompenses, est la matrice des probabilités.
Problèmes possibles[modifier | modifier le code]
- Planification : étant donné un MDP , trouver quelle est une politique qui maximise l'espérance de la récompense.
- Améliorer une politique connue : étant donné une politique , trouver une meilleure politique.
Ce problème est notamment au cœur des algorithmes de recherche de la politique optimale.
- Apprentissage d'une politique sans connaitre le modèle:
- à partir de traces d'exécution: c'est le problème de l'apprentissage par renforcement hors ligne.
- au cours d'expériences sur le modèle, on parle alors d'apprentissage par renforcement en ligne.
Algorithmes[modifier | modifier le code]
Une politique étant fixée, l'équation de Bellman peut se résoudre d'au moins deux manières, permettant donc de déterminer les valeurs de , et par suite, celles de également.
- on peut déjà remarquer que, dans le cas où le nombre d'états est fini, l'équation de Bellman cache en fait un système linéaire de équations à inconnues.
On peut donc le résoudre, une fois traduit en une équation matricielle, par une technique telle que le pivot de Gauss.
- on peut également remarquer qu'en posant
on définit un opérateur , appelé opérateur de Bellman, pour lequel est un point fixe. On peut montrer que est une contraction, ce qui garantit d'une part l'existence d'un unique point fixe, et d'autre part que la suite récurrence converge vers ce point fixe exponentiellement vite.
Équations d'optimalité de Bellman[modifier | modifier le code]
Le but de l'agent est de trouver la politique optimale qui lui permet de maximiser son gain, c'est-à-dire celle qui vérifie, pour tout état , quelle que soit l'autre politique . On peut montrer que la fonction de valeurs optimale vérifie l'équation d'optimalité de Bellman:
De manière analogue, la fonction vérifie elle aussi une équation d'optimalité:
Résolution des équations d'optimalité de Bellman[modifier | modifier le code]
Les équations d'optimalité de Bellman ne sont pas linéaires, il faut donc abandonner l'idée de les résoudre algébriquement. En revanche, l'opérateur de Bellman défini par
définit encore une contraction dont est un point fixe. La fonction de valeurs optimale peut donc à nouveau s'approcher par un processus itératif à convergence exponentielle.
Déterminer la politique optimale: algorithme d'Itération sur la valeur (VI)[modifier | modifier le code]
La méthode itérative que nous venons de voir pour les équations d'optimalité de Bellman fournit un premier algorithme, appelé itération sur la valeur (VI: Value-Iteration) permettant de déterminer . Il suffit en effet de déterminer avec une précision donnée, et on peut en déduire la politique optimale par:
Une difficulté dans cet algorithme est de déterminer la précision avec laquelle calculer de manière à être sûr d'en déduire effectivement la politique optimale.
Déterminer la politique optimale: algorithme d'Itération sur la politique (PI)[modifier | modifier le code]
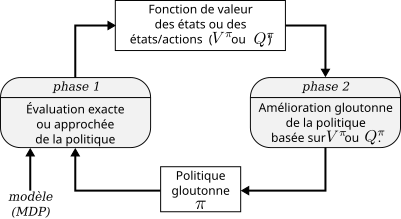
Un autre algorithme, appelé itération de la politique (PI: Policy-Iteration) essaye d'obtenir la politique optimale sans nécessairement calculer «jusqu'au bout» les valeurs de . L'idée est de partir d'une politique quelconque , puis d'alterner une phase d'évaluation, dans laquelle la fonction est déterminée (avec une des techniques vues plus haut), et une phase d'amélioration, où l'on définit la politique suivante par:
- .
Cet algorithme prend fin lorsqu'aucune évolution de la politique n'est observée, ie, lorsque pour tout .
Si dans l'algorithme précédent l'on utilise une méthode itérative pour évaluer , alors se pose la question de savoir à quelle précision s'arrêter. Ce problème n'en est en réalité pas un, car on peut montrer que même si l'on tronque l'évaluation de , l'algorithme converge tout de même vers l'optimal. À l'extrême, c'est-à-dire lorsqu'une seule itération est utilisée pour évaluer , et après avoir réuni en une seule étape de calcul la phase d'amélioration et la phase d'évaluation, on retombe sur l'algorithme VI.
L'algorithme PI peut également se formuler dans les termes de la fonction d'états-actions plutôt que . On voit donc qu'un grand nombre de variantes peuvent être imaginées, mais tournant toutes autour d'un même principe général qui est schématisé à la figure ci-contre.
Articles connexes[modifier | modifier le code]
- Chaîne de Markov, dont dérivent les MDP
- Processus de décision markovien partiellement observables (POMDP), qui permettent de modéliser l'incertitude sur l'état dans lequel on se trouve
- Calcul stochastique, qui est à la base des modèles stochastiques
- Apprentissage par renforcement, méthode permettant de résoudre des processus de décision markoviens
- Métaheuristiques, méthodes utilisant parfois des processus markoviens
Bibliographie[modifier | modifier le code]
- (Puterman 1994) M. L. Puterman, Markov Decision Processes. Discrete stochastic dynamic programming., Wiley-Interscience, New York 1994, 2005.
- (Sutton et Barto 1998) R. S. Sutton et A.G. Barto Reinforcement Learning: An introduction, MIT Press, Cambridge, MA, 1998.
Références[modifier | modifier le code]
- (en) Richard Bellman, « A Markovian Decision Process », Journal of Mathematics and Mechanics, vol. 6, no 5, , p. 679–684 (ISSN 0095-9057, lire en ligne, consulté le ).
- (en) Xianping Guo, Onesimo Hernandez-Lerma, Continuous-Time Markov Decision Processes: Theory and Applications, Springer-Verlag Berlin Heidelberg, 2009, (ISBN 978-3-642-02546-4)









![{\displaystyle T:S\times A\times S\to [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55ad2a126965231d6458bca3bc25459d76d83233)


![{\displaystyle R:S\times A\times S\times \mathbb {R} \to [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ec44df9ec76945a63ccdf0921ef165658d61d77)




















![{\displaystyle \pi :S\times A\to [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48c5e56b78ee044bec6af4437c8b436f1ed5f10)

![{\displaystyle \mathbb {P} [A_{t}=a\mid S_{t}=s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49f614b695b8430c9888aef1be9921a541feb311)



















![{\displaystyle Q^{\pi }(s,a)=\sum _{s'\in S}[R(s,a,s')+\gamma V^{\pi }(s')]T(s,a,s').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de0ba487e8d8ba9d5ab854a4eed7073e8bde698e)

![{\displaystyle V^{\pi }(s)=\sum _{s'\in S}[R(s,\pi (s),s')+\gamma V^{\pi }(s')]T(s,\pi (s),s').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f2f0c6b4a6c680c99e487fecaae77e31fec080b)







![{\displaystyle K(f)(s)=\sum _{s'\in S}[R(s,\pi (s),s')+\gamma f(s')]T(s,\pi (s),s'),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/020a762c0e5b5f360c56243581ce0406e6c3ee53)






![{\displaystyle V^{*}(s)=\max _{a\in A}\sum _{s'\in S}[R(s,a,s')+\gamma V^{*}(s')]T(s,a,s').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c5f51185b219b3c186b2fd3104444e79624a816)

![{\displaystyle Q^{*}(s,a)=\sum _{s'\in S}[R(s,a,s')+\gamma \max _{a'\in A}Q^{*}(s',a')]T(s,a,s').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13b6525bc391b384ba2435b1616eab2b2cb7a263)

![{\displaystyle K^{*}(f)(s)=\max _{a\in A}\sum _{s'\in S}[R(s,a,s')+\gamma f(s')]T(s,a,s'),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ded1b4a794ffca025f588381518adf2a4cb623b6)
![{\displaystyle \pi (s)=\arg \max _{a\in A}Q^{*}(s,a)=\arg \max _{a\in A}\sum _{s'\in S}[R(s,a,s')+\gamma V^{*}(s')]T(s,a,s').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e995e97329a25e80803f1046c5c6486ae1559aa1)


![{\displaystyle \pi _{n+1}(s)=\arg \max _{a\in A}\sum _{s'\in S}[R(s,a,s')+\gamma V^{\pi _{n}}(s')]T(s,a,s').}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d485b3ac9e79fea1eec90efc66f50e0db0043a5)

