Explication avec les mains
Cet article ne cite pas suffisamment ses sources ().
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».
En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?
Ne doit pas être confondu avec Preuve sans mots.
En sciences, une explication est appelée « explication avec les mains » lorsqu'elle esquisse un raisonnement sans présenter une démonstration rigoureuse. Un tel procédé est employé par exemple à l'occasion d'un exposé oral lorsque le temps donné au conférencier est trop court pour détailler complètement l'argumentation ou introduire les prémisses. Pendant le processus de recherche il aide à formuler une conjecture ou à préparer une démonstration rigoureuse en particulier pendant le dialogue avec un collaborateur. En tout état de cause, il ne s'agit pas d'un concept de science exacte, mais d'une attitude de scientifique.
L'expression vient du fait que le chercheur utilise des images, des gestes et des mimiques qui en soutenant un discours cherchent à emporter la conviction de l'auditoire en donnant plus de réalité aux concepts énoncés et en mettant en évidence les points clés du raisonnement. Comme dans cette mise en scène le geste l'emporte sur la parole, la terminologie « explication avec les mains » a été utilisée pour la caractériser.
En mathématiques, certains résultats peuvent être illustrés par une expérience physique, notamment en combinatoire, en théorie des nœuds et plus généralement en topologie[1]. Il s'agit plus alors d'une explication par une image animée.
Notes
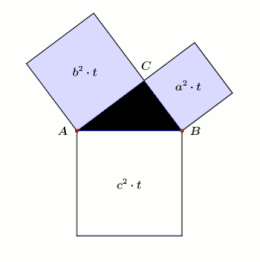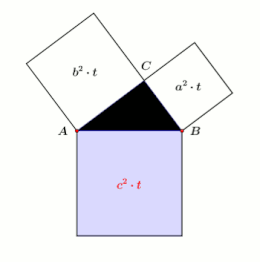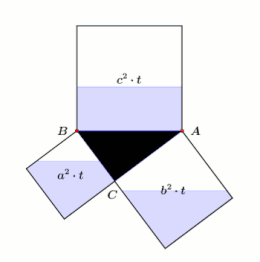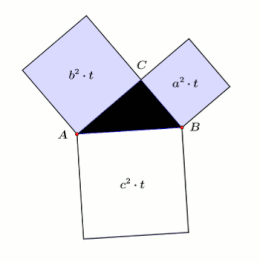
[modifier | modifier le code]- Il s'agit d'une illustration amusante du théorème de Pythagore mais il faut bien garder à l'esprit qu'il s'agit de surfaces et donc, dans cette illustration, de "réservoirs" à 2 dimensions. Alors qu'un réservoir occupe un volume, cette illustration ne doit pas conduire à penser que le théorème de Pythagore est également valide pour les volumes. L'énoncé « Dans tous triangles rectangles, le cube de l'hypoténuse égale la somme des cubes des deux autres côtés » n'est pas vrai. Voir Dernier théorème de Fermat.
Références
[modifier | modifier le code]- Voir par exemple la démonstration en neuf photographies qu'un double tour complet en rotation dans l'espace est homotope à l'identité dans Topology and Geometry de Glen E. Bredon, Graduate Text in Mathematics 139, Springer, 1993, page 166, ou des illustrations analogues dans Quantique : Rudiments, de Jean-Marc Lévy-Leblond, et dont voici une animation en ligne
