Utilisateur:Salle/Bibliographie mathématique

Ceci est actuellement un brouillon pour certains passages de l'article équation.

Quelques problèmes typiques dans l'étude des équations

Comme exposé dans l'introduction, les équations interviennent dans des branches très diverses des mathématiques, et sont de formes variées. Pourtant, un certain nombre de questions soulevées lors de la résolution d'une équation se retrouvent de manière transversales. On se contente ici d'évoquer ces problèmes, enles liant à des exemples qui seront traités dans les paragraphes idoines.

En premier lieu, se posent des questions sur l'existence, l'unicité des solutions à une équation ; et, lorsque l'unicité n'est pas assurée, de compter le nombre de solutions, lorsqu'elles sont en nombre fini, ou de contrôler d'une manière ou d'une autre la taille de l'espace de solutions. Un énoncé typique d'existence et d'unicité concerne la théorie des équations différentielles : c'est la solution des problèmes de Cauchy. Un cas où on peut compter précisément le nombre de solutions est celui d'une équation polynomiale à coefficients complexes. Dans le cas des équations linéaires (y compris différentielles), en dimension finie, les solutions sont souvent en nombre infini, mais on peut estimer ce qu'on appelle la dimension de l'espace des solutions. Dans toutes ces questions, le domaine dans lequel on étudie l'équation joue un rôle primordial (on convient d'ailleurs la plupart du temps qu'une équation est donnée avec le domaine dans lequel les solutions sont étudiées).

Trouver des informations sur le nombre de solutions se distingue du problème qui consiste à identifier ces solutions. Ce dernier problème peut se résoudre de manière exacte ou approchée. Les techniques mises en œuvre pour ces deux types de résolution diffèrent : une résolution approchée fera en général appel à des techniques plus ou moins pointues d'analyse ; le principe d'une résolution exacte est d'exprimer la ou les solutions à l'aide de quelques opérateurs bien identifiés (les quatre opérations arithmétiques et extraction de racines pour les équations polynomiales, auxquelles on ajoute l'opération de primitivation pour les équations différentielles) : ceci est souvent impossible. Ainsi, les mathématiciens qui se préoccupent de résolution exacte sont souvent amenés à étudier les équations d'un autre point de vue : il ne s'agira plus tant de chercher les solutions, que d'étudier les relations entre les solutions, et d'associer à une équation des invariants algébriques contenant une information sur ces relations. L'étude de ces invariants se constitue alors en domaine autonome, et cette formulation est souvent adaptée aux questions de variation du domaine d'étude de l'équation.

Géométrie

Géométrie analytique

Une conique est toujours l'intersection d'un plan et d'un cône de révolution.

En géométrie euclidienne, il est possible d'associer à chaque point de l'espace un jeu de coordonnées, par exemple à l'aide d'un repère orthonormé. Cette méthode permet de caractériser des figures géométriques à l'aide d'équations. Un plan dans un espace de dimension 3 s'exprime comme l'ensemble des solutions d'une équation linéaire de la forme a.x + b.y + c.z + d = 0, où a, b, c et d sont des nombres réels, x, y, z les inconnues qui correspondent aux coordonnées d'un point du plan dans le repère orthonormal. Les valeurs a, b et c sont les coordonnées d'un vecteur perpendiculaire au plan défini par l'équation. Une droite s'exprime comme l'intersection de deux plans, c'est-à-dire comme les solutions d'une équation linéaire à valeurs dans R^{2 ou comme les solutions d'un système de deux équations linéaires à valeurs dans R, si R désigne l'ensemble des nombres réels.}

L'équation cartésienne offre une méthode simple de démonstration du théorème de Thalès relatif au cercle.

Une conique est l'intersection d'un cône d'équation x² + y² = z² et d'un plan. Autrement dit, dans l'espace, toute conique est définie comme les points dont les coordonnées sont solutions d'une équation d'un plan dans R³ et de l'équation précédente. Autrement dit, les coniques sont données comme les lieux des solutions des polynômes de degré 2 à 2 variables.

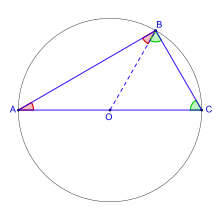
Avec cette approche, on obtient des équations dont l'objectif n'est pas l'expression des solutions au sens du paragraphe précédent. Un exemple est donné par le théorème de Thalès indiquant qu'un triangle est rectangle s'il possède un coté égal à un diamètre d'un cercle et un sommet opposé élément du cercle. Ce théorème est illustré sur la figure de droite. Si le repère est bien choisi, il est orthogonal et l'équation du cercle s'écrit : x² + y² = 1, les points A et C de la figure de droite ont pour coordonnées respectives (-1,0) et (1,0). Dire que AB est perpendiculaire à CB revient à dire que les vecteurs associés sont orthogonaux. L'équation du cercle permet de conclure la démonstration, en effet :

${\overrightarrow {AB}}\cdot {\overrightarrow {CB}}=\langle (x-1,y),(x+1,y)\rangle =(x+1)(x-1)+y^{2}=x^{2}+y^{2}-1=0\quad {\text{car}}\quad x^{2}+y^{2}=1$

L'usage d'une équation permet de faire appel à un nouveau pan des mathématiques pour résoudre des questions de géométrie. Le repère cartésien transforme un problème de géométrie en un problème d'analyse, une fois les figures étudiées traduites en équations ; d'où le nom de géométrie analytique. Ce point de vue, mis en évidence par Descartes, enrichit et modifie la géométrie telle que la concevaient les mathématiciens de la Grèce antique.

Actuellement, le terme géométrie analytique désigne une branche des mathématiques plus avancée qui utilise aussi des outils sophistiqués issus de l'analyse fonctionnelle ou de l'algèbre linéaire.

Équation cartésienne et paramétrique

Il existe au moins deux méthodes pour décrire une figure géométrique à l'aide d'équations. La première consiste à la décrire par une équation de la forme f(x) = 0, où f est une fonction de l'espace euclidien E de dimension n dans R^d où d est un entier plus petit que n. Si f est une fonction suffisamment régulière, n - d est la dimension de la figure géométrique. Si elle est égale à 1, la figure est une courbe, pour 2 on parle de surface etc... Une telle équation peut aussi s'écrire comme système de d équations à valeurs dans les réels exactement comme pour le cas de l'équation linéaire. Ce type d'équation est appelé cartésien si x est exprimé à l'aide de ses coordonnées dans un repère cartésien. Les équations décrites dans le paragraphe précédent sont toutes cartésiennes, comme celle du cercle d'équation x² + y² = 1.

Une autre méthode consiste à décrire la figure géométrique à l'aide d'une fonction f de R^d dans E de la manière suivante, un point m de E est élément de la figure lorsqu'il existe un point x de l'ensemble de définition de la fonction f tel que f(x) est égal à m. Dans ce cas, et sous réserve d'une régularité suffisante de f (il suffit que sa différentielle soit injective), la figure est de dimension d. On parle d'équation paramétrique de la figure géométrique, cette définition de l'équation est relativement éloignée de celle trouvée en algèbre.

Exemple :

Le cercle trigonométrique du plan euclidien admet pour équation paramétrique, de paramètre θ.

$\left\{{\begin{matrix}x&=&\cos \theta \\y&=&\sin \theta \end{matrix}}\right.$

Si la figure est suffisamment régulière, par exemple si elle correspond à une variété, au moins localement, il existe un paramétrage de la figure. Localement signifie que si m est un élément de la figure, il existe une fonction f et un voisinage V d'un point de l'ensemble de départ de f tel que l'image de f soit incluse dans la figure et tel que l'image de V par f soit un voisinage de m dans la figure. Localement, il est aussi possible de définir la figure à l'aide d'une équation cartésienne.

Géométrie algébrique

L'objet de la géométrie algébrique est initialement d'étudier les solutions des équations polynomiales à plusieurs variables, via les considérations de la géomérie analytique telles qu'exposées dans le premier paragraphe : dans le cas de deux variables, le lieu des solutions est une courbe dans le plan, dans le cas de deux variables, c'est une surface dans l'espace, etc. Le degré des polynômes joue aussi un rôle important : dans le cas du degré 1, on retombe sur des problèmes linéaires, déjà évoqués ailleurs dans l'article ; le degré 2 correspond aux coniques, quadriques, etc., très largement étudiées depuis l'Antiquité, en lien notamment avec l'astronomie ; le degré 3 comprend notamment les célèbres courbes elliptiques.

Les coniques et courbes elliptiques sont bien comprises et leur étude élémentaire lorsqu'on considère le problème réel ou complexe. Le premier élément clé pour une étude générale de la géométrie algébrique est ensuite le Nullstellensatz de Hilbert qui permet d'établir un dictionnaire entre les points des objets géométriques définis par une ou plusieurs équations polynomiales, et des objets issus de l'algèbre commutative.une idée au passage : parle-t-on à un moment ou à un autre de l'article des bases de Groebner ?

En revanche, l'étude de ces objets peut être bien plus compliquée dans d'autres cadres ; par exemple, lorsqu'on s'intéresse aux solutions en nombre rationnels, dès l'étude des courbes elliptiques, de nombreuses questions sont aujourd'hui ouvertes sur leur structure : si le théorème de Mordell donne la forme de l'ensemble des solutions (qui a une structure de groupe commutatif), un entier, appelé le rang, qui entre en jeu dans l'estimation de la taille de l'ensemble des solutions, est encore aujourd'hui extrêmement mystérieux, et son comportement fait l'objet de la célèbre conjecture de Birch et Swinnerton-Dyer. Pour les équations de degré supérieur (en fait, plus précisément, de genre supérieur, le genre étant lié outre au degré, à la configuration des points singuliers de la courbe), un théorème des années 1980 dû à Faltings assure la finitude du nombre de solutions à l'équation. Compter ces solutions reste cependant difficile.