Paradoxe de Simpson
| Type | |
|---|---|
| Inventeurs | |
| Nommé en référence à |
Le paradoxe de Simpson ou effet de Yule-Simpson est un paradoxe statistique décrit par Edward Simpson en 1951 et George Udny Yule en 1903, dans lequel un phénomène observé dans plusieurs groupes s'inverse lorsque les groupes sont combinés. Ce résultat, qui semble impossible au premier abord, est lié à des éléments qui ne sont pas pris en compte, comme la présence de variables non indépendantes ou de différences d'effectifs entre les groupes ; il est souvent rencontré dans la réalité, en particulier dans les sciences sociales et les statistiques médicales.
Formulation mathématique[modifier | modifier le code]
Soient f < g deux fonctions mesurables bornées sur un espace de probabilités et supposons que sup (f) > inf (g). Alors on peut trouver deux mesures de probabilités P, Q telles que EP(f) > EQ(g) où EP et EQ désignent l'espérance selon la mesure de probabilités P, resp. Q. L'apparent paradoxe vient du fait que si on prenait l'espérance selon la même mesure de probabilités, par exemple P, on aurait l'inégalité intuitive EP(f) < EP(g).
Formulation en termes de probabilité conditionnelle[modifier | modifier le code]
Considérons deux variables aléatoires, X et Y, et une variable de conditionnement, Z. Le paradoxe de Simpson se produit lorsque la relation entre X et Y est différente dans les sous-groupes de Z par rapport à l'ensemble des données combinées. Soit P(Y|X, Z) la probabilité conditionnelle de Y sachant X et Z. Le paradoxe apparaît lorsque, par exemple, pour un certain x :
pour tous les z, mais :
Ceci peut être expliqué par le fait que :
Lorsque les probabilités P(Y = 1 | X = x, Z = z) varient beaucoup avec z, les pondérer avec P(Z = z | X = x) ou P(Z = z | X ≠ x) peut inverser l'ordre des inégalités. Cette formulation met en évidence l'importance de la prise en compte des variables de confusion potentielles lors de l'analyse des données et sert de rappel que les corrélations observées ne doivent pas être interprétées comme des relations causales sans une analyse plus approfondie. C'est un exemple du paradoxe de Simpson. Oublier le conditionnement peut changer les conclusions d'une étude.
Exemples[modifier | modifier le code]
Résultats scolaires et pratique sportive[modifier | modifier le code]
Pour expliquer le paradoxe de Simpson, imaginons que l'on mesure la performance scolaire de différents élèves en fonction de la quantité de sport pratiqué. Supposons que l'on obtienne les résultats présentés dans le graphique en tête de cet article : l'axe horizontal x (abscisse) représente la quantité de sport pratiqué (par exemple en heures par semaine) et l'axe vertical y (ordonnée) représente la performance scolaire (par exemple, la moyenne des notes sur 10). Dans cet exemple imaginaire, on voit que parmi les élèves « bleus » ceux qui pratiquent davantage de sport sont meilleurs à l'école et il en est de même dans le groupe « rouge ». Pourtant, quand on combine les deux groupes on a une relation inversée qui semble indiquer que plus on pratique de sport (x élevé), moins on obtient de bonnes performances scolaires (baisse sur l'axe y) : l'observation des deux groupes combinés (droite noire en pointillés) semble contredire ce qu'on a observé dans chacun des groupes.
Cet exemple-jouet illustre l'existence de différences entre les groupes (bleu et rouge) dont on n'a pas tenu compte dans l'analyse. En les négligeant, on peut aboutir à des conclusions qui semblent contradictoires. C'est un exemple du paradoxe de Simpson[réf. nécessaire].
Contributeurs de Wikipédia[modifier | modifier le code]

Pour illustrer ce paradoxe de manière plus détaillée, considérons deux contributeurs de Wikipédia : Lisa et Bart. La première semaine, Lisa modifie 60 % des articles qu'elle consulte alors que Bart modifie 90 % des articles qu'il lit. La deuxième semaine, Lisa ne modifie que 10 % des articles lus et Bart 30 %. Les deux fois, Bart possède un taux de modifications supérieur à Lisa.
Pourtant, sur les deux semaines, Lisa a modifié un plus grand pourcentage d'articles que Bart : 55 % contre 35 % pour Bart (chiffres arrondis). Ce paradoxe apparent est dû au fait que dans les chiffres hebdomadaires on n'a pris en compte que le taux de modifications, alors que dans le bilan, on a utilisé en plus le nombre d'articles lus.
La première semaine, Lisa lit 100 articles et en modifie 60 (on retrouve bien 60 % de modifications). Pendant ce temps, Bart modifie 9 des 10 articles qu'il consulte (on retrouve les 90 % de la première semaine). La deuxième semaine, Lisa modifie 1 article sur les 10 lus (10 %) et Bart 30 sur 100 (30 %). Quand les chiffres des deux semaines sont combinés, on constate que les deux contributeurs ont lu autant d'articles (110) mais que Lisa en a modifié 61 contre seulement 39 pour Bart.
| Semaine 1 | Semaine 2 | Total | |
|---|---|---|---|
| Lisa | 60/100 = 60 % | 1/10 = 10 % | 61/110 = 55,45 % |
| Bart | 9/10 = 90 % | 30/100 = 30 % | 39/110 = 35,45 % |
Il apparaît que les chiffres de chaque semaine, pris séparément, soutiennent une hypothèse mais, une fois rassemblés, démontrent l'hypothèse inverse.
D'une manière plus formelle :
- — Lisa modifie 60 % des articles qu'elle lit.
- — Bart modifie 90 % des articles étudiés.
Bart a modifié un plus grand taux d'articles.
- — Lisa modifie 10 % des articles lus.
- — Bart modifie 30 % des articles lus.
Bart a encore dépassé Lisa.
Dans les deux cas, Bart a un pourcentage de modifications supérieur à Lisa. Mais comme en deux semaines, les deux contributeurs ont lus 110 articles chacun, on établit que :
- — Lisa a modifié 61 articles.
- — Bart n'en a modifié que 39.
- — Lisa a modifié plus d'articles que Bart (hypothèse opposée).
Le paradoxe apparent vient du fait que Bart a un taux de modifications supérieur chaque semaine, alors que sur les quinze jours, Lisa a modifié plus d'articles. Dans un cas, on prend en compte le taux de modifications, et dans l'autre, le nombre de modifications.
Les bases mathématiques du paradoxe sont sans équivoque. Si et , on sent que doit être plus grand que . Mais si des pondérations différentes sont utilisées pour obtenir le score final de chaque contributeur, alors cette tendance s'inverse.
Le premier score de Lisa est pondéré : ; de même pour Bart : .
Mais ces poids sont inversés par la suite.
Finalement, la question est de savoir qui est le plus efficace. Lisa semble l'être plus que Bart, puisqu'elle a modifié plus d'articles. Cependant, si on suppose que Lisa n'a fait que des corrections de coquilles et Bart que des modifications complexes concernant la neutralité, on pourrait dire que les 39 modifications de Bart sont plus importantes que les 61 de Lisa. Bart serait alors plus efficace. Le résultat dépend donc de ce que l'on entend par « efficacité ».
Cet exemple démontre que le vocabulaire et le contexte sont importants pour qualifier la notion de succès, concept qui peut être trompeur si l'on s'en tient aux chiffres[réf. nécessaire].
Traitement des calculs rénaux[modifier | modifier le code]
Un exemple réel provenant d'une étude médicale[1],[2] sur le succès de deux traitements contre les calculs rénaux permet de voir le paradoxe sous un autre angle.
Cette table montre le succès des traitements A et B pour soigner petits et gros calculs :
| petits calculs | gros calculs | ||
|---|---|---|---|
| Traitement A | Traitement B | Traitement A | Traitement B |
| 93 % (81/87) | 87 % (234/270) | 73 % (192/263) | 69 % (55/80) |
Dans les deux cas, le traitement A est plus efficace.
Toutefois, si l'on construit un résultat global en additionnant naïvement les traitements de petits et gros calculs, on trouve que B est plus efficace.
| Traitement A | Traitement B |
|---|---|
| 78 % (273/350) | 83 % (289/350) |
Ce qui crée le paradoxe, et l'impression erronée que B est globalement plus efficace, c'est que le traitement A a été donné beaucoup plus souvent pour les gros calculs, qui sont plus difficiles à soigner. Le rebroussement de cette inégalité, qui conduit au paradoxe, se produit à cause de deux effets concurrents :
- La variable supplémentaire (ici la taille des calculs) a un impact significatif sur les rapports, elle a une influence en même temps sur le choix du traitement (les calculs de taille élevée ont été plus souvent traités par le traitement A) et sur le résultat du traitement (les calculs de taille élevée sont plus difficiles à soigner). Cette variable est appelée facteur de confusion.
- Les tailles des groupes qui sont combinés quand la variable supplémentaire est ignorée sont très différentes.
Efficacité des vaccins[modifier | modifier le code]
Le paradoxe de Simpson peut aussi amener à des fausses conclusions sur l'efficacité d'un vaccin. Par exemple, les vaccins contre le Covid-19 sont plus efficaces contre les formes graves de la maladie, sans l'être à 100 %. En France, les vaccins ont été en priorité administrés à des personnes à risque (donc particulièrement susceptibles de développer une forme grave de la maladie)[3], alors que les populations jeunes (peu susceptibles de développer une forme grave de la maladie) restent souvent en grande partie non-vaccinées. En conséquence, la grande proportion de vaccinés parmi les personnes hospitalisées et décédées peut donner l'impression que les vaccins n'ont pas ou très peu d'efficacité contre les formes graves de la maladie, même en tenant compte de la grande proportion de vaccinés parmi la population générale (autrement dit sans commettre l'erreur de l'oubli de la fréquence de base). Mais cette impression est biaisée car il faut tenir compte des caractéristiques démographiques de la population vaccinée, et dans cet exemple les personnes à risque sont surreprésentées. Dans ce cas, une analyse par tranches d'âge permet de constater l'efficacité réelle des vaccins[4],[5].
On peut se convaincre de l'importance de l'effet Simpson avec un exemple poussé à l'extrême : une maladie affecte (ou tue) uniquement des personnes de plus de 60 ans et seules celles-ci sont vaccinées avec un vaccin imparfait. Dans ce cas, tous les décès enregistrés concernent des personnes ayant été vaccinées.
Interprétation géométrique[modifier | modifier le code]
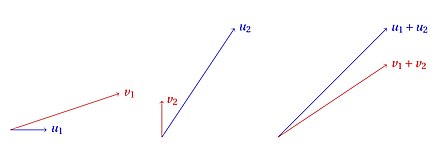
On peut fournir une interprétation géométrique, c'est-à-dire sans mentionner les probabilités, très visuelle du paradoxe de Simpson. Il est possible de considérer des vecteurs , , et du plan vérifiant :
- la pente de est strictement inférieure à celle de ;
- la pente de est strictement inférieure à celle de ;
mais la pente de est strictement supérieure à celle de .
Notes et références[modifier | modifier le code]
- (en) Confounding and Simpson's paradox, Steven A Julious, Mark A Mullee, University of Southampton, 1994
- (en) Charig, Webb, Payne, et Wickham, « Comparison of treatment of renal calculi by open surgery, percutaneous nephrolithotomy, and extracorporeal shockwave lithotripsy. », British Medical Journal, (lire en ligne)
- Conseil d'orientation de la stratégie vaccinale, « Recommandations de vaccination Covid-19 janvier 2021 »
- Swiss National Covid-19 Science Task Force: Rapport scientifique, 23 novembre 2021 (figures 3 et 4)
- Université de Nottingham Trent: Expert blog: In the wrong hands, vaccination statistics can prove deadly - Simpson’s Paradox shows why
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
- Analyse multivariée
- Des résultats paradoxaux assez similaires :
- Effet de structure
- Erreur écologique
- Voyages au pays des maths
Bibliographie[modifier | modifier le code]
- (en) E. H. Simpson, « The Interpretation of Interaction in Contingency Tables », Journal of the Royal Statistical Society, b, vol. 13, , p. 238-241 (lire en ligne)
- N. Gauvrit, Statistiques, Méfiez-vous !, Paris, Ellipses,
- Jean-Paul Delahaye, Au pays des paradoxes, Belin [détail des éditions] (ISBN 978-2-84245090-8), « Le paradoxe de Simpson », p. 115-118
- (en) Bigelow, John, « Simpson’s Paradox », dans The Stanford Encyclopedia of Philosophy, (lire en ligne)
Liens externes[modifier | modifier le code]
- Le paradoxe de Simpson, Denis van Waerebeke, Cédric Piktoroff (réalisation), dans Voyages au pays des maths sur Arte (, 10 minutes) Consulté le .


























