Angles d'Euler
En mécanique et en mathématiques, les angles d'Euler sont des angles introduits par Leonhard Euler (1707-1783) pour décrire l'orientation d'un solide ou celle d'un référentiel par rapport à un trièdre cartésien de référence[1]. Au nombre de trois, ils sont appelés angle de précession, de nutation et de rotation propre[2],[1], les deux premiers pouvant être vus comme une généralisation des deux angles des coordonnées sphériques.
Le mouvement d'un solide par rapport à un référentiel (un avion dans l'air, un sous-marin dans l'eau, des skis sur une pente...) fait intervenir six paramètres, qui sont, par exemple, les trois coordonnées décrivant la position de son centre de masse (ou d'un point quelconque du solide) et les trois angles d'Euler, cf. les schémas ci-dessous.
Les angles d'Euler peuvent aussi servir à représenter l'orientation d'un solide par rapport à un repère (appelée aussi attitude en astronautique).
-
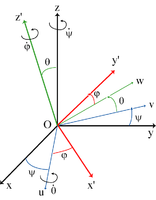
Angles d'Euler ψ, θ et φ. Le référentiel fixe est indiqué en noir, le référentiel mobile en rouge et la ligne des nœuds en bleu.
-
Autre représentation.
Notations et étymologies[modifier | modifier le code]
Les trois angles d'Euler, de précession, de nutation et de rotation propre (ou de giration), sont couramment notés respectivement ψ, θ et φ.
Le mot précession vient du latin praecessio (« action de précéder ») ; cela provient de son utilisation en astronomie dans l'expression « précession des équinoxes ».
Le mot nutation vient du latin nutatio (« action de pencher la tête ») et est aussi utilisé en botanique pour signifier l'habitude qu’ont certaines plantes de pencher leurs fleurs[3].
Le mot rotation vient du latin rotatio avec la même signification et le mot giration vient du latin gyratum, lui-même issu du grec gûros (« cercle »).

Exemple de la toupie[modifier | modifier le code]
Dans l'exemple du mouvement de la toupie ci-contre, l'angle de nutation θ mesure l'obliquité de l'axe par rapport à la verticale, l'angle de précession ψ mesure la rotation de l'axe de la toupie autour de Oz, et l'angle de rotation propre φ mesure bien la rotation de la toupie sur elle-même.
On voit dans cet exemple que l'angle de précession ψ est égal à la longitude augmentée d'un angle droit et l'angle de nutation θ est égal à la colatitude dans les coordonnées sphériques de l'axe Oz' dans Oxyz.
Rotations d'Euler[modifier | modifier le code]
Changement de référentiel[modifier | modifier le code]
Les trois rotations obtenues en modifiant un des trois angles d'Euler et en gardant les deux autres constants sont la précession, la nutation et la rotation propre. On passe du référentiel fixe Oxyz au référentiel lié au solide Ox'y'z' par trois rotations successives :
- La précession, d'angle ψ autour de l'axe Oz, qui fait passer de Oxyz au référentiel Ouvz (en bleu dans l'image de gauche ci-dessus).
- La nutation, d'angle θ autour de l'axe Ou (ou ligne des nœuds), qui fait passer de Ouvz à Ouwz' (en vert).
- La rotation propre, ou giration, d'angle ϕ autour de l'axe Oz', qui fait passer de Ouwz' au référentiel lié au solide Ox'y'z' (en rouge).
NB. L'axe Ou est porté par l'intersection des plans Oxy et Ox'y'.
Les coordonnées (x', y', z') d'un point dans le référentiel mobile Ox'y'z' sont reliées aux coordonnées (x, y, z) de ce même point dans le référentiel fixe Oxyz par la relation suivante[4] :
avec la matrice de passage [5]
Rappelons que cette matrice donne aussi verticalement les coordonnées des vecteurs unitaires dans la base .
Notons que le passage inverse s'écrit , où AT est la transposée de A, cette dernière étant orthogonale.
Interprétation par composée de rotations[modifier | modifier le code]
La matrice A est aussi la matrice dans le référentiel fixe Oxyz de la rotation r transformant ce référentiel en Ox'y'z'. La décomposition de matrices A = BCD montre que cette rotation est la composée où
- r1 est la rotation d'angle ϕ autour de Oz,
- r2 est la rotation d'angle θ autour de Ox,
- r3 est la rotation d'angle ψ autour de Oz.
Généralité de la décomposition[modifier | modifier le code]
La donnée des deux référentiels Oxyz et Ox'y'z' permet de connaitre les angles d'Euler. Celui de nutation θ est l'angle entre Oz et Oz', l'axe Ou s'obtient comme perpendiculaire commune à Oz et Oz', et on obtient respectivement ψ et ϕ comme angles entre Ox et Ou et entre Ou et Ox'.
La matrice A ci-dessus est donc la matrice générale d'une rotation, et la décomposition prouve que le groupe des rotations d'axe passant par O est engendré par les rotations d'axes l'un de deux axes orthogonaux donnés passant par O.
En terme d'aéronautique, cela signifie qu'on obtient l'orientation quelconque d'un avion en utilisant deux des trois rotations : roulis (d'axe la carlingue), tangage (d'axe les ailes), et lacet (d'axe la verticale), par exemple roulis puis tangage puis roulis.
Autre conséquence : lorsqu'on manipule à la souris un objet visualisé à l'écran (vers le haut : rotation autour de l'horizontale, vers la droite : rotation autour de la verticale), on obtient toutes les orientations possibles de l'objet.
Nota : r est la rotation d'angle α autour de où
- ,
et a pour coordonnées .
On obtient la première relation en écrivant que la trace de A est égale à 1 + 2 cos α.
La deuxième et la troisième deuxième s'obtiennent facilement en écrivant les matrices d'Euler-Rodrigues de et en effectuant leur produit.
Exemple : la rotation d'un tiers de tour autour de (1 , 1 , 1) de matrice a pour angles d'Euler .
Mécanique du solide[modifier | modifier le code]

On s'intéresse seulement ici à la description du mouvement du solide en rotation quelconque autour du point O, qui peut être un point fixe du solide dans le référentiel de référence ou le centre de masse. Les angles d'Euler sont choisis de façon à permettre une mémorisation simple de la construction du vecteur rotation instantané du solide, nécessaire à l'étude de la cinématique du solide. Le vecteur rotation instantané du solide est en effet donné par la simple somme :
- ,
où les vecteurs apparaissant dans le membre de droite sont les vecteurs unitaires des axes correspondants et les expressions sont respectivement les vitesses angulaires de précession, de nutation et de rotation propre. On remarquera que l'expression simple précédente utilise une base non orthogonale.
L'utilisation des angles d'Euler est très générale en mécanique et en astronomie, par exemple pour décrire le mouvement du gyroscope : dans l'animation ci-contre, les vitesses de précession et de rotation propre sont constantes et la vitesse de nutation est nulle, l'angle de nutation restant constant.
Orientation cristalline[modifier | modifier le code]

En science des matériaux, les angles d'Euler sont utilisés pour décrire l'orientation cristalline (orientation d'un cristallite par rapport aux axes de l'échantillon), notamment dans le domaine de la texture (orientation préférentielle). Les angles sont alors en général[7] notés () avec :
- ;
- ;
- .
On utilise parfois une autre variante dans laquelle la seconde rotation (nutation) se fait selon l'axe Ov au lieu de Ou ; les angles sont alors notés () sans que cela ait un rapport avec les notations des mécaniciens, ce qui n'est pas sans risque de confusion.
Notes et références[modifier | modifier le code]
- Taillet, Villain et Febvre 2018, s.v.angles d'Euler, p. 30.
- Pérez 2014, p. xxi et 275.
- « Nutation », sur Wiktionnaire
- « Les angles d'Euler », sur Physique et simulations numériques, Faculté des Sciences exactes et naturelles, Université du Maine
- (la) Leonhard Euler, « Problema algebraicum ob affectiones prorsus singulares memorabile », Commentatio 407 Indicis Enestoemiani, Novi Comm. Acad. Sci. Petropolitanae 15, , la "matrice" se trouve page 83 (lire en ligne)
- Liss KD, Bartels A, Schreyer A, Clemens H, « High energy X-rays: A tool for advanced bulk investigations in materials science and physics », Textures Microstruct., vol. 35, nos 3/4, , p. 219–52 (DOI 10.1080/07303300310001634952)
- il s'agit de la notation adoptée par Bunge dans son ouvrage Texture analysis in materials science, une référence dans le domaine
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- [Lehning 2007] H. Lehning, « Les angles d'Euler », dans H. Lehning (dir.), Leonhard Euler : un génie des Lumières, Paris, Pôle, coll. « Biblioth. Tangente » (no 29), , 1re éd., 1 vol., 154, ill. et portr., 17 × 24 cm (ISBN 978-2-8488-4066-6, EAN 9782848840666, OCLC 470945066, BNF 41041045, SUDOC 11449309X), dossier no 2, art. no 8, p. 64-65.
- [Pérez 2014] José-Philippe Pérez (avec la collaboration d'Olivier Pujol), Mécanique : fondements et applications, Paris, Dunod, hors coll., , 7e éd. (1re éd. ), 1 vol., XXVI-801, 17,5 × 24 cm (ISBN 978-2-10-071232-8, EAN 9782100712328, OCLC 892897104, BNF 43887529, SUDOC 180751727, présentation en ligne, lire en ligne).
- [Taillet, Villain et Febvre 2018] R. Taillet, L. Villain et P. Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Sup., hors coll., , 4e éd. (1re éd. ), 1 vol., X-956, ill. et fig., 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, SUDOC 224228161, présentation en ligne, lire en ligne), s.v.angles d'Euler, p. 30, col. 1-2.