Algorithme de Grover
En informatique quantique, l’algorithme de Grover est un algorithme de recherche, permettant de rechercher un ou plusieurs éléments qui répondent à un critère donné parmi éléments non classés en temps proportionnel à et avec un espace de stockage proportionnel à . Il a été découvert par Lov Grover en 1996[1].
Dans les mêmes conditions (recherche parmi des éléments non classés), un algorithme classique ne peut faire mieux qu'une recherche dans un temps proportionnel à , en testant successivement le critère sur chaque élément. L'étendue de la gamme de critères pouvant être utilisée par cet algorithme lui donne un caractère universel, ce qui en fait un des algorithmes les plus importants et potentiellement le plus utile de l'informatique quantique.
L'exemple classique d'utilisation de cet algorithme est la recherche, dans un annuaire téléphonique ordinaire classé alphabétiquement, du nom qui correspond à un numéro de téléphone donné. L'algorithme de Grover fonctionne toujours en lui présentant les nombres entiers de 1 à N, représentant dans le cas de l'annuaire une position dans ce dernier. Le critère de sélection est dans ce cas : la position correspond à un numéro de téléphone donné. La position étant connue, on en déduit le nom ou toute autre information liée à la position.
Plus généralement, l'ensemble des nombres entiers de 1 à N peut indexer un ensemble de solutions possibles à un problème. Dans ce cas, s'il est possible de vérifier rapidement qu'une solution résout un problème (ce qui est généralement le cas, et ce qui définit même toute une classe importante de problèmes dits de complexité NP), alors il est possible à l'aide de cet algorithme d'accélérer notablement la recherche des solutions de ces problèmes par rapport à la recherche brute.
Parmi les problèmes dans NP (et même NP-complet) qui pourraient être résolus par cet algorithme se trouvent notamment :
- le problème SAT ;
- la coloration de graphe ;
- la détermination d'un chemin hamiltonien dans un graphe ;
- des puzzles, cryptographiques comme « SEND+MORE=MONEY », ou numériques comme le sudoku.
Malgré tout, ce genre de problème est souvent de complexité exponentielle par rapport au nombre d'éléments du problème (typiquement, si n est le nombre d'éléments mis en jeu dans le problème). Même si cet algorithme apporte une optimisation non négligeable (quadratique) par rapport à une recherche brute, il transforme un problème de complexité en , qui demeure exponentielle.
Certains algorithmes classiques, adaptés à un problème particulier, peuvent faire mieux, surtout si on tolère une solution approximative, ou probabiliste. Mais cet algorithme présente le double avantage d'être généraliste (dès que l'on a l'algorithme pour vérifier une solution, on a automatiquement l'algorithme pour trouver la solution), et de garantir de trouver la ou les solution(s) optimale(s).
Il a été prouvé en 1999, par Christof Zalka[2], que l'algorithme de Grover est l'algorithme quantique le plus efficace pouvant traiter le problème de la recherche non structurée. Il est impossible de faire mieux qu'une amélioration quadratique de la complexité, en utilisant le parallélisme du calcul quantique.
Principe de l'algorithme[modifier | modifier le code]
Rappels et notations[modifier | modifier le code]
En calcul quantique, l'information est codée par des qbits, qui possèdent comme tout objet quantique la particularité de pouvoir être simultanément dans deux états différents notés et [3]. Cet état superposé est un vecteur, combinaison linéaire des deux états , et étant deux scalaires complexes.
Un ensemble de qbits chacun dans un état superposé forme globalement une superposition de états : . Ce vecteur est normé, de sorte que .
Les lois de la mécanique quantique interdisent d'avoir une information complète sur un état quantique, et donc de déterminer toutes les valeurs En fait, lors d'une mesure de cet état intriqué, l'état va être projeté aléatoirement sur un et un seul état, vecteur propre de l'instrument de mesure caractérisé par son Observable , ce avec une probabilité respective de .
Le calcul quantique va calculer simultanément résultats, et ceci de manière parfaitement déterministe car l'équation de Schrödinger, et donc l'évolution du vecteur d'état, est déterministe. Mais on ne peut avoir directement accès à tous les résultats, car l'observation ne donne accès qu'à une seule configuration, prise au hasard parmi toutes les configurations, en détruisant le reste de l'état quantique. Néanmoins, le calcul peut être réalisé de manière à donner à l'état intéressant une probabilité proche de 1 et le reste une probabilité négligeable, et mesurer ainsi avec certitude le résultat recherché. C'est exactement ce qui va se passer pour l'algorithme de Grover où une phase « d'amplification » cherche à rendre déterministe le résultat recherché.
Présentation générale de l'algorithme[modifier | modifier le code]
L'algorithme de Grover incorpore deux éléments principaux :
- Une « boîte noire », ou Oracle, qui détermine si un des états de la superposition
() donné en entrée correspond à un certain critère. C'est l'état "cible" de la boite noire. Cette boîte noire permet de particulariser l'algorithme à un problème donné. - Un algorithme d'amplification d'amplitude, qui permet de rendre exploitable et mesurable l'information donnée par la boîte noire. Cet algorithme est indépendant de la boîte noire, et c'est cette procédure qui nécessite itérations. La sélection de l'état cible par la boite noire est instantané, en tout cas en , mais il est impossible de récupérer instantanément l'état cible sélectionné.
La boîte noire est définie mathématiquement par une fonction qui identifie si un état « » vérifie un certain critère :
Cette boîte noire est bien entendu en mesure d'accepter une superposition d'états en entrée, et donc de vérifier le critère simultanément pour tous les états de la superposition. En effet, la boîte noire est elle-même implémentée par un calcul quantique, qui est en mesure d'opérer sur une superposition d'un bout à l'autre d'algorithme qui détermine le critère.
Le propos de l'algorithme est maintenant le suivant : étant donné un état initial équi-superposé[4] de tous les états possibles de qbits :
comment la boîte noire va-t-elle influencer cet état pour donner un résultat mesurable ? Pour pouvoir mesurer le résultat, et trouver ainsi le résultat en une seule opération, l'état final doit être :
afin de mesurer avec une quasi-certitude l'état , qui a été signalé par la boîte noire.
Pour aboutir à ce résultat, l'algorithme de Grover procède ainsi (on suppose dans cet exemple qbits, ce qui donne états superposés, et l'état à rechercher est l'état 6) :
- Préparation d'un état équi-superposé
- L'algorithme fait en sorte que la boîte noire inverse la phase de l'état (ou des états) qui vérifie le critère
- L'algorithme applique ensuite un opérateur d'amplification d'amplitude, qui effectue un miroir des amplitudes autour de la moyenne des amplitudes. Cela a pour effet d'amplifier l'état cible, et de diminuer les autres états (voir schémas)
- On itère au total les étapes 2 et 3, fois, pour obtenir l'état final
-
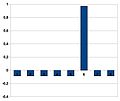
1 : État initial
-
2 : Application de l'oracle
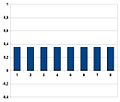
-
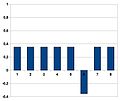
3 : Application de l'opérateur « miroir autour de la moyenne »[5]
-
3 : État amplifié
-
4 : État final, après une itération supplémentaire
L'état peut être alors mesuré pour obtenir, avec une quasi-certitude, l'état recherché.
Remarques et éléments complémentaires[modifier | modifier le code]
Nombre d'itérations. Optimalité du nombre d'itérations[modifier | modifier le code]
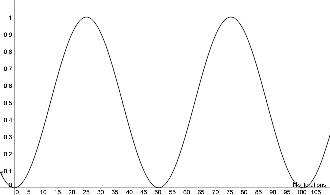
Le nombre d'itérations optimal est exactement de , N étant le nombre de qbits (voir Détermination du nombre d'itérations optimal). Au-delà de ce nombre, la probabilité de détection commence à décroître. C'est pourquoi C.P. Williams, dans son livre Explorations in Quantum Computing, aime citer l'épouse d'un informaticien quantique qui compare l'algorithme de Grover à la cuisson d'un soufflé : il est nécessaire d'arrêter l'algorithme ni trop tôt ni trop tard.
La probabilité de détecter la solution est non nulle dès la première itération et s'accroît à chaque itération. Serait-il possible d'accélérer le processus en s'arrêtant (par exemple) à itérations, vérifier si le résultat mesuré est une solution (ce qui est rapide), sinon tout recommencer pour de nouveau itérations, etc.? Est-ce que, en moyenne, ce processus ne serait pas plus rapide que de faire à chaque fois le nombre d'itérations optimal ? Le calcul montre que cette stratégie nécessite, en moyenne, le même nombre d'itérations que le nombre optimal, sans compter le coût de réinitialiser le dispositif à chaque échec[Williams 1].
Applications de l'algorithme de Grover[modifier | modifier le code]
L'algorithme de recherche de Grover est très polyvalent : l'opérateur qui identifie les solutions du problème (l'Oracle) étant clairement dissocié du reste de l'algorithme, il peut être utilisé pour des problèmes très divers, et notamment pour les problèmes de complexité NP (voir introduction).
On peut également utiliser l'Oracle à d'autres niveaux, pour non pas rechercher directement des solutions, mais pour chercher des heuristiques de solutions. Par exemple, il est en théorie possible d'utiliser l'algorithme de Grover pour accélérer les algorithmes probabilistes classiques[Williams 2]. Dans un algorithme probabiliste, on utilise successivement plusieurs graines de générateur de nombres pseudo-aléatoires : certaines graines vont s'orienter vers la solution, d'autres graines vont faire diverger l'algorithme. On s'arrête après l'essai successif d'un certain nombre N de graines, dès qu'une même solution semble être désignée par plusieurs graines, alors que les autres graines donnent des résultats très différents. L'algorithme de Grover peut donner les mêmes résultats, en exploitant une superposition de graines, en étapes seulement[6].
Dans un autre domaine, l'algorithme de Grover peut être utilisé, non pour faire des recherches de solution, mais uniquement pour ses capacités d'amplification d'amplitude. Les chercheurs en physique quantique ont souvent le besoin de préparer un objet quantique dans un état particulier, ce qui est en général extrêmement difficile. L'algorithme de Grover permet de fabriquer un état quantique donné, en n'amplifiant que les composantes voulues par l'expérimentateur[7].
Récursivité de l'algorithme de Grover et traitement des problèmes NP-Complets[modifier | modifier le code]
Il est en théorie, et en pratique, possible d'utiliser l'algorithme de Grover lui-même dans l'Oracle, menant à une certaine forme de récursivité de l'algorithme.
Cette forme de récursivité s'applique particulièrement bien aux problèmes NP-Complets dont la recherche de solution s'effectue souvent en descendant un arbre de recherche[Williams 3]. Au lieu de rechercher la solution parmi toutes les solutions terminales de l'arbre, ce qui mène à une complexité brute de (contre pour un algorithme classique), il est possible d'obtenir une complexité de (avec un facteur inférieur (voire très inférieur) à un, dépendant du problème considéré) en appliquant l'algorithme de Grover aux niveaux successifs de l'arbre. La complexité demeure toujours exponentielle, mais l'amélioration est telle que l'algorithme quantique est alors en mesure d'être meilleur que les meilleurs algorithmes classiques pour résoudre ces problèmes NP-Complets[Williams 4].
Détails d'implémentation de l'algorithme[modifier | modifier le code]
Opérateur de Grover[modifier | modifier le code]
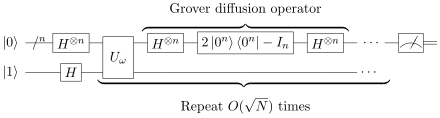
L'opérateur quantique itéré, dit « opérateur de Grover », s'exprime sous la forme suivante :
- est l'Oracle ( sur la figure ci-contre).
- est l'opérateur (ou transformation) de Hadamard, qui est un opérateur de base en calcul quantique. Il est tel que .
Il possède la propriété de transformer un état pur en un état superposé, et réciproquement. - est l'opérateur « Zero phase shift » défini comme ( étant l'opérateur identité).
- est appelé l'opérateur de diffusion de Grover.
Opérateur de diffusion de Grover (miroir autour de la moyenne)[modifier | modifier le code]
C'est , qui va inverser les états autour de la moyenne (voir présentation générale de l'algorithme). En effet :
- est l'état équi-superposé initial.
En appliquant cet opérateur à un état quelconque :
Chaque amplitude est transformée ce qui constitue en effet un miroir de l'amplitude autour de la moyenne des amplitudes.
Détermination du nombre d'itérations optimal[modifier | modifier le code]
Il existe plusieurs démonstrations du nombre optimal d'itérations . Certaines effectuent une interprétation géométrique de l'opérateur de diffusion de Grover, faisant apparaître une analogie entre cet opérateur et une rotation progressive du vecteur d'état de l'état initial vers l'état cible. L'état initial et l'état cible étant orthogonaux, il suffit de compter le nombre de rotations pour aboutir à une rotation totale de [Williams 5]. On peut également, plus algébriquement, calculer combien d'inversions autour de la moyenne sont nécessaires pour aboutir à un maximum, en partant d'une distribution uniforme .
Voici une démonstration du calcul du nombre d'itérations, par la méthode géométrique[8].

Soit l'état initial équi-superposé :
On peut remarquer que cet état peut se décomposer en la somme ( étant l'état cible recherché) :
avec
et où et sont des vecteurs normés à un. La figure ci-contre représente alors l'état dans cette base, où est l'angle entre . D'après cette représentation, on obtient naturellement .
On remarque aussi que, selon cette représentation, l'opérateur effectue une symétrie du vecteur par rapport à , puisque l'Oracle inverse uniquement la composante de .
Selon cette représentation, tout opérateur quantique va provoquer une rotation d'un vecteur représenté dans cette base (les opérateurs quantiques étant unitaires, l'image d'un vecteur par un opérateur sera toujours sur le cercle unité). Quel est l'angle de rotation que va faire subir l'opérateur de Grover vu plus haut, à un état quelconque ?
Soit , et . On a donc, d'après la formulation de vue plus haut :
Donc :
Donc, l'opérateur effectue, dans cette représentation, une rotation d'angle , tel que .
Muni de ce résultat, il suffit maintenant de calculer combien de rotations sont nécessaires pour passer de à , c'est-à-dire pour une rotation totale de .
On doit avoir :
- .
Pour des valeurs de N suffisamment grandes (ce qui est normalement le cas d'utilisation de l'algorithme de Grover..), on peut approcher :
d'où :
- .
Bibliographie[modifier | modifier le code]
- Colin P. Wiliams Explorations in Quantum Computing Springer 2011 :
- Paragraphe 5.6 « Can Grover's Algorithm Be Beaten ? »
- Paragraphe 5.7.1 « Speeding Up Randomized Algorithms »
- Paragraphe 7.4 « Quantum Solution Using Nested Grover's Algorithm »
- Paragraphe 7.5 « Summary »
- Voir par exemple 5.4.1 « How Much Amplitude Amplification is Needed to Ensure Success ? »
Notes et références[modifier | modifier le code]
- Grover L.K. : A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212
- C Zalka Grover's Quantum Searching Algorithm is Optimal Phys. rev. A, Volume 60 Issue 4 (1999) pp. 2476-2751
- Se rappeler le Chat de Schrödinger
- C'est-à-dire que, si on mesure cet état, on a une chance égale de mesurer n'importe quel état de la superposition
- La ligne orange est la moyenne des amplitudes bleues. Le sommet des valeurs vertes (finales) et bleues sont symétriques par rapport à cette ligne.
- A. Carlini et A. Hosota Quantum Probabilistic Subroutines and Problems in Number Theory Phys. Rev. A, Volume 62 (2000)
- L.K Grover Synthesis of Quantum Superpositions by Quantum Computation Phys. Rev. Lett. Volume 85 Issue 6 (2000) pp. 1334-1337
- Voir Présentation de l'algorithme de Grover par le Pr. Raffaele Solca






























![3 : Application de l'opérateur « miroir autour de la moyenne »[5]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3b/Grover-MiroirMoyenne.jpg/120px-Grover-MiroirMoyenne.jpg)