Utilisateur:PCIFRV/Brouillon

Les technologies océanologiques actuelles permettent d’enregistrer des observations régulières infra-jour ou infra-horaire. Il est important de stocker à des fins d’analyse. Or cette masse de données nécessite une compression qu’il faut maîtriser pour ne pas perdre d’information. Un grand nombre de représentations des séries temporelles ont été proposées dans la littérature.

L’objectif est de répondre à la question suivante d’un point de vue théorique et pratique sur un cas concret : quelle(s) représentation(s) est la plus adaptée pour mettre en évidence des événements intermittents et extrêmes dans des données physico-chimiques issues de bouées marines toutes les 20 minutes.

Introduction[modifier | modifier le code]

Les océanographes imaginent et mettent au point des technologies océanologiques permettant d’enregistrer, d’analyser et d’étudier un très grand nombre de domaines concernant les océans et les mers. Ces systèmes développés en amont des relevés ou des expériences, ont pour objectif de capter le maximum de données le plus précisément possible tout en évitant les incidents techniques (perte de données, mémoire saturée, mauvais enregistrements…) et en faisant face aux imprévues (événements météorologiques, pollution, phénomènes extérieures…).

En effet, aujourd’hui, les technologies océanologiques rendent possible l’enregistrement d’observations régulières, périodiques ou non périodiques, pour des phénomènes se déroulant selon certaines conditions temporelles. Ces observations régulières sont donc infra-jour ou infra-horaire, dont l’intérêt est dans détecter ses événements automatiques.

Le stockage de ces informations est essentiel pour l'exploitation et l’analyse des ressources océaniques et la protection des environnements marins. Devant le flux important de données et pour éviter les pertes d’information, il est nécessaire de construire une méthodologie de compression de ces informations.

Les séries temporelles permettent d'observer les évolutions des environnements océanographiques et marins. Ces séries constituent un grand volume de données et contiennent des informations complexes et d'intérêt. L'objectif majeur de cet article est de trouver la meilleure représentation des séries temporelles et de détection des événements automatiques.

Terminologie[modifier | modifier le code]

Le traitement du signal est défini comme l’ensemble des connaissances scientifiques et technologiques qui permettent la réalisation d’une chaîne d’acquisition et de traitement de l’information. C’est donc une discipline d’importance au sein des sciences de l’ingénieur, où se rencontrent des savoir-faire mathématiques, électroniques et informatiques, et des problèmes physiques d’origines très diverses (mécanique, génie électrique, biomédical, optique, acoustique, radar, sonar …).

Les signaux[modifier | modifier le code]

Qu'est ce qu'un signal ?[modifier | modifier le code]

On appelle un signal une fonction d’une ou plusieurs variables engendrées par un phénomène physique. Les signaux sonores, par exemple, correspondent à de faibles variations de pression qui se propagent dans l’espace, et de percevoir l’information dont ils peuvent être porteurs. Dans la plupart des cas pratiques, la variable d’évolution est le temps, et la notion de signal se rapporte davantage à un transfert d’information qu’à un transfert d’énergie. Ainsi, la plupart des signaux manipulés de nos jours correspondent à l’évolution temporelle de tensions électriques délivrées par des capteurs.

Classification des signaux[modifier | modifier le code]

A cette notion de signal est associée plusieurs modes de caractéristiques qui précisent le phénomène observé, la façon de l’étudier, et les moyens technologiques mis en œuvre :

Signaux continus[modifier | modifier le code]

La notion de continuité sert à décrire les phénomènes qui ne changent pas de valeur brutalement mais évoluent progressivement. Plus mathématique, une fonction continue en un point est telle que :

$\lim _{t\rightarrow t_{0}}{x(t)}=x(t_{0})$

Elle est continue sur l’intervalle $I=[a;b]$ si elle est continue pour tout $t\in I$ .

Les signaux continus sont aussi appelés en ingénierie des signaux analogiques.

Signaux discrets[modifier | modifier le code]

Par opposition au signal continu, le signal discret n’est connu qu’en un certain nombre de points constituant une suite discrète de mesure nulle :

$\{t_{i}\}\rightarrow \{x(t_{i})\}$

La suite peut comporter un nombre infini d’éléments, la seule condition est que la suite soit de mesure nulle.

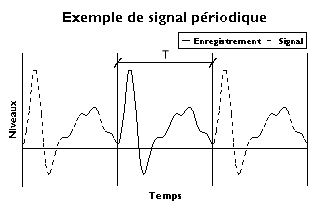
Signaux périodiques[modifier | modifier le code]

Les signaux périodiques peuvent être continus ou discrets, ils sont caractérisés par leur période $T$ telle que :

$x(t+nT)=x(t);n\in \mathbb {Z^{*}}$

Cette périodicité peut s'observer graphiquement par la répétition infinie d'un motif identique. Le support de ce motif représente la période entre deux motifs identiques.

Si $T$ est une période alors les $kT,k\in \mathbb {N^{*}}$ sont aussi des périodes acceptables. Cependant, pour compresser un signal périodique, il est préférable de trouver le plus petit motif qui se répète afin de retenir un minimum d'information.

La fréquence correspond au nombre de périodes par unité de temps : $f={\frac {1}{T}}$

L’unité SI de f est le hertz : $1Hz=1s^{-1}$

La fréquence correspond au nombre de motifs apparus pendant une unité de temps (typiquement la seconde).

Signaux causaux[modifier | modifier le code]

Un signal causal est un signal nul pour $t<0$ , n’a de valeurs non nulles que pour $t\in \mathbb {R} ^{*}$ et est de la forme générale :

$x(t)=heaviside(t)e(t)$

Signaux à énergie finie[modifier | modifier le code]

Un signal est à énergie finie si l’intégrale $\int _{-\infty }^{+\infty }|x(t)|^{2}dt$ converge.

La totalité des signaux de la nature sont des signaux à énergie finie. Un groupe important est celui des signaux transitoires. Mais il y a aussi les signaux de valeur bornée et de durée finie (support borné) dont la décroissance n’est pas naturelle mais qui sont des signaux tronqués du type de l’équation.

Signaux indépendants[modifier | modifier le code]

Deux signaux sont indépendants s’ils n’ont jamais échangé d’énergie, quel que soit leur décalage. Cette indépendance peut se montrer aisément à l'aide de la corrélation ou d'une régression. Des signaux indépendant sont peu corrélés et ont une mauvaise régression. Des signaux interdépendants ont une corrélation élevée et ont une bonne régression.

Caractéristiques des signaux[modifier | modifier le code]

Le contenu d'un signal[modifier | modifier le code]

Le contenu d'un signal correspond à l'aire de la surface comprise entre l'axe des abscisses et les valeurs prises par le signal.

Pour un signal continu, le contenu $C$ d'un signal $x(t)$ est défini comme étant l'intégrale du signal $x(t)$ :

$\int _{-\infty }^{+\infty }x(t)dt$

Pour un signal discret, le contenu $C$ d'un signal $x_{k}$ est défini comme étant la somme du signal $x_{k}$ :

$\sum _{k=-\infty }^{+\infty }x_{k}$
Le contenu n'est pas nécessairement fini. Réellement, les signaux sont toujours à contenus finis puisqu'ils sont étudiés sur des intervalles de temps fini.

Le contenu est une caractéristique linéaire sur l'espace des signaux continus et discrets car l'intégrale et la somme sont des opérateurs linéaires.

Une définition plus localisée du contenu peut être utilisée comme un outil de compression des signaux.

L'énergie d'un signal[modifier | modifier le code]

En traitement du signal, on introduit la notion d'énergie de signal. Si on appelle ${\displaystyle E_{S}}$ l'énergie d'un signal ${\displaystyle x(t)}$ où ${\displaystyle x}$ est une fonction du temps ${\displaystyle t}$ , on calculera son énergie par la relation :

${\displaystyle E_{S}=\int _{-\infty }^{+\infty }|x(t)|^{2}dt}$

L’énergie ainsi définie est fortement analogue à la définition physique de l'énergie. Cette définition fait intervenir la somme des carrés de la valeur absolue de chacun des termes de la série.

A partir du constat précédent, l'énergie d'un signal discret peut s'écrire :

$E_{S}=\sum _{k=-\infty }^{+\infty }|x_{k}|^{2}$

La puissance d'un signal[modifier | modifier le code]

Pour les signaux à énergie infinie comme les signaux périodiques, il est beaucoup plus pertinent d'utiliser pour caractéristique la puissance. Cette quantité se construit à partir de l'énergie générée $E_{s}$ pendant une période $T$ .

$P_{T}={\frac {E_{s}}{T}}$

Les normes et les distances[modifier | modifier le code]

Définition d'une norme[modifier | modifier le code]

La norme est une extension de la valeur absolue des nombres aux vecteurs. Elle permet de mesurer la longueur commune à toutes les représentations d'un vecteur dans un espace affine, mais définit aussi une distance entre deux vecteurs invariante par translation et compatible avec la multiplication externe.

La norme est une application $N$ qui vérifie les trois hypothèses suivantes :

Séparation : $\forall x\in E,N(x)=0\Rightarrow x=0_{E}$
Absolue homogénéité : $\forall (\lambda {},x)\in K\times E,N(\lambda {}x)=|\lambda {}|N(x)$
Sous-additivité : $\forall (x,y)\in E^{2},N(x+y)\leq N(x)+N(y)$

Les normes utilisées dans le traitement du signal sont les normes p.

Normes associées aux signaux[modifier | modifier le code]

La norme de la convergence uniforme[modifier | modifier le code]

La norme de la convergence uniforme correspond à la norme infinie qui est défini comme suit :

$||x||_{\infty }=\sup _{t\in S}|x(t)|$

La version discrète s'obtient facilement en changeant de mesure :

$||x||_{\infty }=\sup _{k\in \mathbb {Z} }|x_{k}|$

La norme de convergence retourne la valeur de l'amplitude absolue la plus grande. Les valeurs du signal sont entièrement incluses dans l'intervalle $[-||x||_{\infty },||x||_{\infty }]$ .

La norme de la convergence moyenne[modifier | modifier le code]

La norme de la convergence moyenne se construit par analogie à la norme 1. Celle-ci est définie ainsi :

$||x||_{1}=\int _{S}|x(t)|dt$

La version discrète a pour forme :

$||x||_{1}=\sum _{k=-\infty }^{+\infty }|x_{k}|$

La norme de convergence moyenne correspond au contenu du signal en valeur absolue. Le contenu est inclus dans l'intervalle $[-||x||_{1},||x||_{1}]$ .

La norme de la convergence quadratique[modifier | modifier le code]

La norme de la convergence quadratique est inspirée de la norme 2 euclidienne. La norme euclidienne est définie par :

$||x||_{2}={\sqrt {\int _{S}|x(t)|^{2}dt}}$

Et sa version discrète est :

$||x||_{2}={\sqrt {\sum _{k=-\infty }^{+\infty }|x_{k}|^{2}}}$

La racine étant plutôt gênante, on manipule le carré de cette norme appelé quadrance. Celle-ci n'est pas une norme. On remarquera que la quadrance d'un signal représente exactement son énergie.

$||\alpha {}x||_{2}=|\alpha {}|.||x||_{2}$ mais $E_{S}(\alpha {}x)=|\alpha {}|^{2}E_{S}(x)$ donc l'énergie n'est pas une norme.

Définition d'une distance[modifier | modifier le code]

Une application $d$ est dite distance si et seulement si elle vérifie les trois propriétés suivantes :

Symétrie : $d(x_{1},x_{2})=d(x_{2},x_{1})$
Inégalité triangulaire : $d(x_{1},x_{3})\leq d(x_{1},x_{2})+d(x_{2},x_{3})$
Séparation : $d(x_{1},x_{2})=0\Leftrightarrow x_{1}=x_{2}$

Les applications de la forme $d_{p}(x_{1},x_{2})=||x_{1}-x_{2}||_{p}$ sont des normes.

Distances associées aux normes de signaux[modifier | modifier le code]

Distance de la convergence uniforme[modifier | modifier le code]

La distance de convergence uniforme $d_{\infty }$ indique le plus grand écart observable qu'il y a entre deux signaux.

Distance de la convergence moyenne[modifier | modifier le code]

La distance de convergence moyenne $d_{1}$ mesure l'écart entre les deux signaux terme à terme.

Distance de la convergence quadratique[modifier | modifier le code]

La distance de convergence quadrique $d_{2}$ mesure l'écart quadratique entre les deux signaux.

Les erreurs se mesurent en écart donc en distance.

Séries temporelles[modifier | modifier le code]

Les séries temporelles constituent une part importante des données produites, elles se retrouvent dans plusieurs domaines tels que la finance, la météorologie, le son etc.

Les principaux axes d’études autour des séries temporelles qui ont été proposés dans la littérature sont les suivants :

La prédiction : étant donnée une série temporelle $X=x_{1},x_{2},...,x_{T}$ contenant $T$ points, il s’agit de prédire la ou les valeurs suivantes, c’est-à-dire les valeurs $X_{t+1},X_{t+2},X_{t+3},...$
La classification : étant donnée une série temporelle $X$ , il s’agit de l’assigner à une des (deux ou plus) classes prédéfinies.
La complétion : étant donnée une série temporelle $X=x_{1},x_{2},...,x_{T}$ contenant $T$ points et un masque $m_{i}$ tel que $m_{i}=1$ si la valeur de $x_{i}$ est connue et $m_{i}=0$ sinon. Il s’agit d’inférer la ou les valeurs manquantes, c’est-à-dire les valeurs pour lesquelles $m_{i}=0$ .
L’indexation : étant donnée une série temporelle $X$ ainsi qu’une mesure de similarité (ou dissimilarité) notée $D(X,X,0)$ , tel que $D(X,X,0)$ est grand si les séries $X$ et $X_{0}$ sont similaires et petites. Sinon, il s’agit de trouver la ou les séries temporelles les plus similaires dans une base de données donnée.
La détection d’anomalies : étant donnée une série temporelle $X$ que l’on considère comme étant "normale", le but est de déterminer quelles séries au sein d’une base de données contiennent une "anomalie ».

Contexte[modifier | modifier le code]

Une anomalie est l’écart relatif entre des valeurs d’un élément métrologique par rapport à sa valeur normale. Concrètement, une anomalie est une perte de la vraie information.

Un signal porte de nombreuses informations dont les plus connues sont le contenu, l’énergie, les pics, les extremums, les bornes. Ainsi pour un signal, une anomalie est la perte d’au moins l’une de ces informations. C’est pourquoi à chaque nouvelle représentation des signaux proposée dans la littérature, les problématiques et les démonstrations portent sur les mêmes sujets.

Par exemple, si nous prenons la décomposition en série de Fourier, nous avons d’abord la définition des coefficients. Puis, nous trouvons un théorème de conservation de l’énergie (Egalité de Parseval) et des théorèmes de conservation du contenu (Théorème de Dirichlet). Enfin, il présente des anomalies (l’effet Gibbs).

L’intérêt de créer de nouvelles représentations réside, d’une part, dans la concision de la représentation, et d’autre part, dans la conservation des informations : C’est typiquement de la compression sans perte. Les compressions sans pertes n’introduisent donc pas d’anomalie. A partir de ce genre de représentation, il est possible de resynthétiser le signal original sans anomalie.

Par exemple, si nous prenons la transformée de Fourier discrète, il est possible de passer d’une représentation temporelle réelle à une représentation fréquentielle dans le domaine de Fourrier. Et puisque nos deux espaces sont en bijection, la transformation s’effectue sans perte d’information. Il est donc possible de resynthétiser le signal temporel réel à partir de sa transformée. La conversion s’effectue sans perte mais la transformée n’est pas nécessairement plus concise que le signal original.

En réalité, pour obtenir des signaux concis, il est courant de sacrifier volontairement certaines informations : C’est une compression avec perte. Ces signaux compressés possèdent donc de nombreuses anomalies. La synthèse du signal original à partir du signal compressé est nécessairement imparfaite.

Pour mesurer théoriquement l’écart entre le signal réel et le signal synthétisé, il faut des indicateurs. Ceux-ci sont couramment utilisés dans la littérature comme les normes $L_{0}$ , $L_{1}$ , $L_{2}$ , $L_{\infty }$ . Dans la vie de tous les jours, nous ne connaissons jamais le signal original, comme celui-ci a engendré le signal compressé, il est donc impossible de mesurer l’écart par rapport à la réalité. En revanche, puisque les représentations sont testées sur les espaces classiques (Espace de Lebesgue $L^{p}$ , Espaces continues), il en général possible de définir une enveloppe autour du signal compressé dans laquelle se trouve notre signal réel.

Retrouver le signal original à partir du signal compressé est un problème inverse mal posé typique. Pour retrouver le signal original parmi l’ensemble des signaux solutions du problème inverse, il faut des informations supplémentaires (gamme capteur, forme du signal émis, …) souvent obtenus par un expert (gamme experte, expérience, à priori, …).

Les anomalies ne sont pas nécessairement gênantes, tout dépend de l’usage attendu pour le signal. Par exemple, pour un travail sur l’énergie du signal, il possible de voyager de représentation en représentation tant que des théorèmes assurent la conservation de l’énergie : la conservation des autres caractéristiques importe peu.

C’est donc à l’opérateur de définir les informations caractéristiques qu’il souhaite conserver.

Problématique[modifier | modifier le code]

Ces dernières années ont été marquées par l’explosion de la quantité de données temporelles dans différents domaines tels que la météorologie et la biologie entre autres. Ces données sont produites sous la forme de séries temporelles qui exhibent le plus souvent des dépendances spatio-temporelles, infra-jour ou infra-horaire. Or cette masse de données nécessite une compression qu’il faut maîtriser pour ne pas perdre d’information.

Un grand nombre de représentations des séries temporelles ont été proposés dans la littérature. Les séries temporelles sont particulières comparées aux autres types de données statistiques, car elles tiennent à la présence d’une relation d’antériorité qui permet d’ordonner l’ensemble des informations. Les séries temporelles constituent un exemple simple de la thématique de l’estimation et la prévision des processus stochastiques. Les dates d’observations sont souvent équidistantes les unes des autres : on a des séries mensuelles, trimestrielles, etc.

La problématique qui se pose ici est de déterminer quelle représentation de séries temporelles est la plus adaptée pour mettre en évidence des événements intermittents et extrêmes dans des données physico-chimiques issues de bouées marines toutes les 20 minutes.

L’objectif est principalement de répondre à la problématique d’un point de vue théorique et pratique sur un cas concret. Nous nous proposons d’utiliser des techniques d’apprentissage de représentation en particulier pour traiter ces problèmes.

Etude comparative[modifier | modifier le code]

Cas concret[modifier | modifier le code]

Premier abord aux séries temporelles[modifier | modifier le code]

En statistique, la règle générale et primordiale consiste à commencer par regarder les données, avant d’effectuer le moindre calcul.

Cette série a un aspect très irrégulier. Ses fluctuations irrégulières ont parfois une amplitude très élevée.
La série n'est pas périodique.
La série possède des périodes de grandes amplitudes et des périodes de très faible amplitude. Ses périodes semblent apparaître de manière récurrente.

Cette liste de remarques n’est certainement pas exhaustive. Mais elle a pour but de traduire simplement quelques comportements que l’on retrouve sur la plupart des séries temporelles. Puisque notre ambition est de d´écrire et d’analyser ce genre de données, il nous faut donc proposer des modèles de représentations qui respectent au mieux le jeu de données et qui intègrent les différentes caractéristiques que nous venons de relever.

Classification des représentations[modifier | modifier le code]

Les représentations temporelles sont très utilisées pour la compression des données. Elles sont de la même manière et en général utilisées pour réduire la dimension d’une série temporelle. Cette réduction entraîne une multiplication d’informations sur les caractéristiques de forme fondamentales.

L’un des principaux avantages de ces représentations temporelles, est le traitement du bruit, permettant un filtrage de celui-ci, tout en conservant le maximum d’informations. Dans tous les signaux représentés, l’élimination du bruit est d’une importance capitale pour le gain d’informations. Les zones de bruit peuvent représenter dans certains cas un critère de mesure pour caractériser un signal et étalonner la fiabilité des informations récupérées.

Plus la quantité d’informations augmente, plus l’espace mémoire doit être important, d’une part pour ne pas saturer l’espace, et d’autre part pour garder les informations dans un état stable. Une surcharge pourrait entraîner des pertes ou encore des données faussées. Les représentions temporelles répondent à ce problème en réduisant considérablement la dimension des besoins en mémoire. Le deuxième avantage de cette approche, est de réduire dans le même temps la complexité informatique, notamment pour les méthodes d’apprentissage automatiques conséquentes.

Pour comprendre le phénomène de représentation des séries temporelles ou chronologiques, les méthodes de présentation sont en général classées en quatre catégories ou groupes. Ceux-ci sont présentés ci-dessous, ainsi que les fonctions qui y sont associées, implémentées dans le package R TSrepr.

Non adaptatif[modifier | modifier le code]

Les paramètres de transformation sont inchangés quel que soit la nature de série temporelle utilisée. Ce type est « non adaptif » aux données.

Voici les méthodes de représentation pour ce type :

PAA (approximation agrégée par morceaux)
DWT (transformée en ondelettes discrètes)
DFT (transformée de Fourier discrète)
DCT (transformée en cosinus discrète)
PIP (points importants perceptuels)
SMA - Moyenne mobile simple

Dans le package R :

PAA - Approximation d'agrégats par repr_paa
DWT - Transformée en ondelettes discrète repr_dwt
DFT - Transformée de Fourier discrète repr_dft
DCT - Transformée en cosinus discrète repr_dct
SMA - Moyenne mobile simple repr_sma
PIP - Points d'importance perceptuelle repr_pip

Données adaptatives[modifier | modifier le code]

Seul les paramètres de transformation peuvent varier indépendamment du reste des autres caractéristiques, sauf des données disponibles. Lorsque cette méthode est utilisée, l’hypothèse que la série chronologique observée a été conçue selon un certain modèle basique est émise. Cette approche de la représentation repose uniquement sur cette hypothèse.

Pour représenter les séries temporelles, il est nécessaire de trouver les paramètres d’un certain modèle, eux-mêmes récupérés sous forme de représentation. Pour synthétiser, le type de méthode de présentation dite de « données adaptatives » est la considération que deux séries peuvent être similaires et qu’elles utilisent un même ensemble de paramètres d’un modèle de base.

Voici les méthodes de représentation pour ce type :

SAX (approximation d'agrégats symboliques)
PLA (approximation linéaire par morceaux)
SVD (décomposition en valeurs singulières)

Dans le package R :

SAX - Approximation d'agrégats symboliques repr_sax
PLA - Approximation linéaire par repr_pla

Dictées par les données[modifier | modifier le code]

Ce type d’approches sont dites « dictées par les données » car le taux de compression de la série est défini automatiquement dépendant de la série temporelle brute (dans forme non compressée).

Par exemple, les séries chronologiques dites « écrêtées ». Lorsque la série est représentée de manière écrêtée, un lissage est nécessaire pour raboter les dents de scie du signal de la série brute, l’apparence visuelle est alors bien meilleure. L’objectif est de pouvoir en résumer la série et rendre compte de son état. Il existe deux méthodes de lissages : « moyennes échelonnées » et les « moyennes mobiles ». La première nécessite de récupérer la moyenne échelonnée d'ordre p d'une série dont celle-ci consistera à remplacer la valeur de chaque période p par la moyenne des p périodes. L’inconvénient de cette méthode est la perte de données.

La seconde méthode consiste à utiliser les moyennes mobiles afin de lisser directement la série sans hypothèse a priori sur la forme du modèle sous-jacent. Cette méthode est donc valable quel que soit le modèle de décomposition. Pour cette raison, l’objectif est de classer ce type de lissage dans les méthodes non-paramétriques (par opposition aux méthodes paramétriques). L’un des principaux avantages de cette méthode est la simplicité de mise en œuvre. Elle permet aussi, c’est pour cette raison qu’elle est très utilisée, de mettre en évidence l'allure de la tendance en supprimant certains composants en atténuant le bruit.

Ce type de représentations dispose de moins de méthodes développées de présentation. Cependant, l’une des méthodes en général utilisée est l'écrêtage. Celle-ci consiste à supprimer une partie de l'amplitude d'un signal d’une série temporelle. Un redressement est alors effectué afin de supprimer les alternances négatives. En revanche, elles peuvent être considérées comme un cas particulier de l'écrêtage. L’objectif de cette méthode est donc de réaliser une représentation au niveau du bit.

Dans le package R, on trouve plusieurs fonctions d’extraction de fonctionnalités permettant d’affecter aux données une certaine représentation :

Les fonctions de type FeaClip : Extraction de fonctionnalités à partir d'une représentation découpée repr_feaclip , clipping
Les fonctions de type FeaTrend : Extraction d’entités à partir de la représentation des tendances repr_featrend, trending
Les fonctions FeaClipTrend : Extraction de fonctionnalités à partir de la représentation repr_feacliptrend et des tendances repr_feacliptrend

Basées sur un modèle[modifier | modifier le code]

Cette méthode consiste à représenter comme son nom l'indique, une représentation calquée sur un modèle bien précis. Par exemple, un modèle linéaire, c’est en réalité un modèle d’ARMA (modèles autorégressifs et moyenne mobile), l’un des plus connus et principaux modèles de séries temporelles, que l’on appelle également modèle de Box-JENKINS. Ce modèle est un outil pour comprendre et éventuellement prédire les futures valeurs d’une série temporelle X_t..

Comme son nom l’indique (AR : autorégressifs et MA : moyenne mobile (mobile average en anglais)), ce modèle est composé de deux parties. Sa notation générale ARMA(p,q), présente l’indice p, l'ordre de la partie AR, et q l'ordre de la partie MA. ARMA est donc un combiné de ces deux modèles.

Dans le package R :

Toutes les fonctions de types profil saisonnier : moyen – médian : repr_seas_profile
Toutes les représentations saisonnières basées sur un modèle basé lui même sur un modèle linéaire dit additif, comme par exemple : LM, RLM, L1, GAM : repr_lm , repr_gam
Fonction de coefficients saisonniers du lissage exponentiel repr_exp

Analyse[modifier | modifier le code]

Dans cette partie nous allons procéder à l'analyse des différentes représentations possibles.

Non adaptatif[modifier | modifier le code]

Piecewise Aggregate Approximation (PAA)[modifier | modifier le code]

Les techniques de traitements de données telles que le clustering, la classification etc. sont appliquées sur les données de séries temporelles, permettent de récupérer des informations utiles et des connaissances de ces types de bases de données. Il existe différents types de données temporelles liées à la recherche, comme la recherche de séries temporelles similaires, la dimensionnalité, la réduction, segmentation et la recherche dans le temps.

Le mode de représentation des séries temporelles est utilisé afin de réduire la dimension des données d'origine.

Une autre méthode avancée consiste à utiliser la valeur moyenne de chaque segment pour représenter l'ensemble de données correspondant aux points dans la série temporelle. L’approximation agrégée par morceaux (PAA) dans laquelle la moyenne segmentée des données de début et de fin, des points de chaque segment, est à prendre en considération. Par exemple, une série temporelle de $n$ points et ayant $p$ segments alors sa représentation PAA est :

${\frac {n}{p}}$

Une autre version étendue appelée approximation constante adaptative par morceaux (APCA), dans laquelle la longueur de chaque segment est non fixé, mais est adaptative à la forme de la série.

On notera que la différence entre PAA et APCA est qu’APCA peut identifier le segment de longueur variable.

Transformée en Ondelettes Discrète (DWT)[modifier | modifier le code]

Les DWT (Discrete Wavelet Transform en anglais) est une technique pour la décomposition des signaux discrets dans le temps. Elle est basée sur l’analyse multi-résolution de codage de sous-bande, appelé auparavant « codage pyramidal ».

Les problèmes de redondance de la CWT, reposant sur un principe assez diffèrent de DWT, est la conséquence de la création de celle-ci. Comme la formule utilisée pour la construction des ondelettes est doublement continue. La DWT correspond à une discrétisation judicieuse du plan temps-échelle, ce qui permet d’éviter d’une part, les problèmes de redondance générée par la CWT, et d’autre part, la simplification des calculs d’intégrales de la transformée en ondelettes continue, d’où la création de la Transformée en Ondelettes Discrète.

La transformée en ondelettes discrète (DWT) est obtenue par échantillonnage des coefficients d’échelle et de temps. Pour obtenir les coefficients de la DWT, la formule suivante est utilisée :

$DWT_{\psi }x(j,k)=T_{\psi }x(a=2^{j},b=k2^{j})=2^{\frac {-j}{2}}\int _{-\infty }^{+\infty }x(t)\psi {}(2^{-j}t-k)dt$

Certaines de ses ondelettes peuvent être générées par analyse multi-résolution. L’objectif de la transformée en ondelettes est de choisir une ondelette suffisamment bien adaptée à la fonction $x$ à étudier pour qu’un minimum de coefficients $DWT(x(j,k))$ soient non nuls.

On utilise les décompositions suivantes pour déterminer l’ondelette choisi pour compresser la série temporelle :

$y_{haut}[k]=\sum _{n}x[n].g[2k-n]$

$y_{bas}[k]=\sum _{n}x[n].h[2k-n]$

Dans chaque exemple de la transformée en ondelettes, il y a seulement un nombre fini de coefficients d'ondelette pour chaque région rectangulaire bornée dans le demi-plan supérieur. Il est toujours nécessaire d’évaluer une intégrale pour calculer chaque coefficient d’ondelette.

Rappel et résumé : Comme vu dans la partie précédente, la transformée de Fourier discrète (DFT) indique les composantes fréquentielles d’un signal, moyennées sur toute la durée du signal. Tandis que La transformée en ondelettes discrète (DWT) présentée ici, fournit des informations sur les composants de fréquence (en réalité, de base) et permet également d'indiquer l'heure à laquelle ces composants se produisent.

Ci-dessous, nous allons énoncer les principaux avantages par rapport à la CWT (qui n’est pas présentée ici) et inconvénients par rapport la DFT présenter précédemment :

Les principaux avantages :

Par rapport à la CWT

Bien que la transformée en ondelettes continue discrétisée permet le calcul de la CWT par des ordinateurs, elle n'est pas une vraie transformée discrète. En fait, la série d'ondelettes est simplement une version échantillonnée de la CWT, et les informations qu’elle fournit sont fortement redondantes en ce qui concerne la reconstruction du signal. Cette redondance exige une quantité significative de temps et de ressources de calcul.

La DWT, basée sur l’analyse multi-résolution fournit des informations suffisantes pour l'analyse et la synthèse du signal original, en réduisant significativement le temps de calcul. Comparée à la CWT, il est considérablement plus facile d’implémenter la DWT.

Par rapport à la DFT :

En plus de donner plus d’informations sur les données représentées, la DWT semble être beaucoup flexible pour la compression de ces séries. En effet, il existe de nombreux types différents de bases DWT, DFT qui sont construites seulement avec des cosinus et sinus de fréquences différentes. Comme les données sont fragmentées en plusieurs composants, il devient beaucoup plus facile de filtrer une forme d'onde non stationnaire donnée.

De plus, le filtrage du bruit d'un phonème, en utilisant un simple masque binaire dans le domaine DWT, est mieux appréhendé.

Les principaux inconvénients :

Par rapport à la DFT :

En utilisant la DWT, Il est d’abord plus difficile d'interpréter les résultats car elle contient plus d’informations. Il est parfois très difficile de choisir quelle base utiliser. En effet, une plus grande complexité se traduit dans ce cas en davantage de ressources nécessaires pour effectuer le calcul. De ce fait, la localisation les événements dans le temps ou si le signal est stationnaire dans le domaine fréquentiel, le DWT ne présente aucun avantage. La théorie des DWT est bien plus difficile à comprendre que l’approche de la DFT.

Transformée de Fourier Discrète (DFT)[modifier | modifier le code]

DFT (Discrete Fourier Transform) est l’une des applications les plus importantes dans l'analyse de corrélation, de la transformation du spectre et du filtrage linéaire. Certains algorithmes spéciaux sont développés pour une mise en œuvre plus facile de DFT. Ceux-ci permettent d’avoir un gain de temps de calcul considérable : ce sont les algorithmes FFT.

En principe, pour calculer la DFT, on sait par avance que celle-ci dispose d’une taille N, représentant le nombre composite. L’objectif sera de réduire cette taille à la plus petite DFT pour effectuer le calcul. En général, les algorithmes de calcul sont élaborés lorsque la taille N est une puissance de 2 et de la puissance de 4.

Similairement, la FFT est une transformée « rapide » de la DFT. Celle-ci est souvent utilisée pour le traitement d'images, surtout dans son domaine de fréquence plutôt que le domaine spatial. Comme la FFT, la DFT est l'un des outils les plus importants dans le traitement d'image notamment pour décomposer une image en ses composantes de sinus et de cosinus.

Dans cette méthode, comme le signal d’entrée est dans le domaine spatial, la sortie de la transformation représente le signal dans le domaine des fréquences. Les points de la courbe dans le domaine fréquentiel représentent chacun une fréquence particulière contenue dans la représentation du domaine spatial.

En termes mathématique, l’une des dimensions d’une DFT est donnée par :

$\forall u\in \{0,1,...,N-1\},F(u)={\frac {1}{N}}\sum _{x=0}^{N-1}f(x)e^{-{\frac {j2\pi {}ux}{N}}}$

La DFT inverse :

$\forall x\in \{0,1,...,N-1\},f(x)={\frac {1}{N}}\sum _{x=0}^{N-1}F(u)e^{+{\frac {j2\pi {}ux}{N}}}$

La DFT a deux variables est appelé à DFT à deux dimensions et est donnée par :

$\forall u\in \{0,1,...,N-1\};\forall v\in \{0,1,...,M-1\};F(u,v)={\frac {1}{MN}}\sum _{x=0}^{M-1}\sum _{x=0}^{N-1}f(x,y)e^{-j2\pi {}({\frac {ux}{N}}+{\frac {vy}{M}})}$

La DFT inverse est donnée par :

$\forall x\in \{0,1,...,N-1\};\forall y\in \{0,1,...,M-1\};f(x,y)={\frac {1}{MN}}\sum _{x=0}^{M-1}\sum _{x=0}^{N-1}F(u,v)e^{+j2\pi {}({\frac {ux}{N}}+{\frac {vy}{M}})}$

La transformée de Fourier discrète (DFT) indique donc que les composantes fréquentielles d’un signal sont moyennées sur toute la durée du signal. Elle est la version discrétisée du spectre et à le même nombre d'échantillons dans le signal. FFT est également une DFT, mais le nombre d'échantillons pris est égal à une puissance de 2 pour accélérer le calcul. Le domaine de la transformation de Fourier est complexe. Par conséquent, pour traiter un domaine réel, DCT est utilisé pour la compression.

Les DFT présentent quelques avantages pour la représentation et la compression des séries temporelles. Elles sont beaucoup plus faciles à comprendre et plus intuitives. De plus, l’utilisation de cette représentation n’est pas coûteuse en ressources nécessaires, en calcul et ne requiert pas beaucoup de mémoire et/ou de cycles de processeur et / ou de temps. Par exemple, son utilisation est optimale pour localiser les événements dans le temps ou si le signal est stationnaire dans le domaine fréquentiel.

L’un des principaux désavantages de la DFT est qu'elle est simplement basée sur des cosinus et sinus de fréquences différentes (ou manière équivalente, d'exponentielles complexes de fréquences différentes). Comme les données sont fragmentées en plusieurs composants, il devient beaucoup plus facile de filtrer ou de filtrer une forme d'onde non stationnaire donnée. Son utilisation est donc réduite pour compresser une série temporelle.

Transformation en Cosinus Discrète (DCT)[modifier | modifier le code]

DCT (Discrete Cosine Transform en anglais) est une transformation de la transformation de Fourier, de la même manière que la transformée de Fourier discrète DFT (voir le chapitre suivant). Cependant, cette transformation utilise uniquement des fonctions cosinus au lieu d'utiliser l’assemblage des fonctions cosinus et sinus. Celle-ci permet de convertir le signal d'entrée du domaine temporel dans le domaine fréquentiel, ce qui met en évidence la périodicité du signal.

Par exemple, c'est généralement utilisé pour la compression d’image JPEG et pour la compression vidéo au format MPEG.

Ce type de représentations pour une série chronologique X de longueur n est définie comme :

$X_{f}=K(f)\sum _{i=1}^{n}x_{i}\cos {\frac {\pi {}f(i-0.5)}{n}},f=0,...,n-1$

Avec :

$K(0)={\frac {1}{\sqrt {n}}}$

$K(f)={\sqrt {\frac {2}{n}}},f\in \{1,...,n-1\}$

On peut calculer tous les coefficients avec $O(n\log {n})$ et les opérations d'une manière similaire à l'algorithme de transformée de Fourier rapide (FFT).

Contrairement aux autres représentations, une représentation par DCT dispose des avantages suivants :

Les coefficients sont toujours des nombres réels, par opposition aux coefficients complexes DFT, ce qui diminue le nombre d’erreurs.

DCT peut traiter des signaux bien avec les tendances, alors que DFT souffre du problème « de fuite spectrale » lors de la représentation des « tendances » simples. De plus, on observe la présence d’énergie dans toutes les fréquences.

DCT réalise une meilleure concentration de l'énergie de DFT. En effet, les valeurs successives sont fortement corrélées.

Il faut noter aussi que cette méthode compare sa performance optimale étroitement à la Karhunen-Lo. Ce théorème permet d’affirmer que l’on peut représenter un processus stochastique comme combinaison linéaire infinie de fonctions orthogonales. Cette représentation est analogue à une représentation en série de Fourier.

En revanche, l'inconvénient majeur de cette transformation est que les fonctions de base sont très longues.

Par exemple : Si un coefficient de transformation est quantifié, l'effet est visible dans toute la représentation. Si cela ne semble pas créer de problèmes pour les coefficients de basse fréquence qui sont codés avec précision, les coefficients haute fréquence sont quantifiés grossièrement, et donc la qualité reconstruite de la représentation sur les bords aura une mauvaise qualité.

Deuxièmement, le signal est généralement un signal non stationnaire où différentes parties de la représentation ont différentes propriétés statistiques. Alors si la transformation est calculée sur l’ensemble de la série, cette non-stationnarité sera perdue, entraînant une mauvaise performance de compression de cette série temporelle.

Points Perceptuellement Importants (PIP)[modifier | modifier le code]

L’identification des PIP permet une très grande réduction en termes de dimension de la série temporelle et de conservations des principales caractéristiques de ses données.

La représentation entre PIP proches ou adjacents permet de définir explicitement des relations entre les points de la série temporelle.

Le mappage entre ces règles de représentation permet de distinguer les différents types de tendances entre les PIP des séries temporelles et de trouver la représentation par une séquence de caractères, ce qui facilite l'identification des caractères.

Après l'identification des PIP d’une série temporelle, la détection des motifs est faite selon deux méthodes différentes, l'une est basée sur des modèles, l’autre sur des règles. La première méthode permet de définir les modèles des motifs visuellement, on a donc une comparaison très précise entre la série temporelle et les modèles. Concernant la deuxième méthode, chaque motif est défini par un ensemble de règles de telle sorte que l’on puisse décrire sa forme,où ces règles sont créées en fonction des relations entre les points perceptuellement importants, les PIP.

Simple moving average (SMA)[modifier | modifier le code]

SMA est une méthode de prévision dans laquelle tous les poids de la valeur réelle récente utilisés pour les prévisions sont égaux. Malgré sa simplicité, SMA est l’une des méthodes quantitatives utilisées afin de déterminer la tendance d’une série temporelle.

Selon cette méthode, la demande prévue pour la période suivante est égale à la demande totale pour un certain nombre de périodes passées, divisé par le nombre de périodes.

La n période de la moyenne mobile utilise la valeur des n dernières périodes permettant de prévoir la prochaine valeur de période.

Un grand nombre de valeurs réelles récentes rendent la prévision plus stable. En revanche un petit nombre de valeurs réelles récentes rend la prévision plus sensible.

La moyenne mobile simple suppose que la demande est stable et n’implique aucun facteur saisonnier. Cette méthode de prévision de la période suivante est égale à la quantité totale de production pour un certain nombre de données divisé par le nombre (la longueur) de la période. $Moyenne\_mobile={\frac {Demande\_totale\_pour\_un\_certain\_nombre\_de\_donnees\_recentes}{Nombre\_de\_donnees}}$

Par exemple, pour la prévision utilisant quatre valeurs récentes et réelles, la somme totale des valeurs de ces périodes sera calculée puis divisée par quatre, ensuite l’ancienne valeur sera ignorée et les nouvelles données seront ajoutées à la fin de la liste.

La méthode de la moyenne mobile simple présente des avantages et des inconvénients. De nombreux avantages sont constatés lors de l’exécution de la SMA car:

Elle est facilement calculée;
Elle n'exige pas beaucoup de données du passé;
Elle est facile à comprendre;
Elle supprime les "mauvaises" données après n périodes.

En revanche, les inconvénients que présente la méthode de la moyenne mobile simple :

La prévision des résultats dépend de la longueur de la moyenne; il convient donc de choisir la période appropriée pour le calcul de la prévision;
SMA nécessite de conserver toutes les données du passé, ce qui entraîne des coûts plus élevés pour la sauvegarde et la récupération des données, manuellement ou par ordinateur;
Cette méthode donne le même poids ou la même signification à toutes les données utilisées pour le calcul de la valeur prévisionnelle;
Les tendances ne peuvent pas être bien prévues.

Données adaptatives[modifier | modifier le code]

Symbolic Aggregate approXimation (SAX)[modifier | modifier le code]

On définit des épisodes comme des intervalles du domaine de définition des séries temporelles, celles-ci permettent de réduire la dimensionnalité en regroupant les points des séries temporelles. A cause du coût minime d’acquisition et de stockage des données, les séries temporelles sont alors enregistrées dans les bases de données sous une forme très détaillée, qui ne dépend pas de l’échelle de temps à laquelle se développent les comportements à déterminer. Il n’y aura donc aucune perte d’informations essentielles lors du regroupement des points en épisodes, d’où le principe de la représentation symbolique SAX.

Cette représentation se caractérise par :

un domaine temporel qui est divisé en épisodes de même taille

Des classes d’équivalence des valeurs prises par les séries temporelles qui sont déterminées à partir du nombre de symboles à utiliser, afin d’obtenir un découpage en classes de même effectif sous afin que la distribution centrée et réduite des valeurs soit normale.

La représentation symbolique SAX présente les avantages suivants :

sa construction est efficace en temps de calcul, pour la représentation d’une série temporelle de N points

les représentations basées sur un même nombre de symboles et des épisodes de même taille sont trivialement commensurables (relatif à plusieurs grandeurs dont toutes sont des multiples entiers d'une autre grandeur)

En revanche, cette représentation comporte des inconvénients qui sont intrinsèquement liés :

l’erreur de modélisation est très importante car le modèle n’est pas localement adapté aux données

les classes d’équivalence ne sont pas pertinentes car elles ne sont pas adaptées aux données.

Approximation Linéaire par Morceaux (PLA)[modifier | modifier le code]

L’approximation linéaire par morceaux (PLA) pour les données de séries temporelles est un problème classique de compression de données et du suivi du signal qui date depuis les années 1960.

En raison de la présence omniprésente de données et de dispositifs de collecte qui capturent de façon continue presque chaque mesure de la source de données: température, humidité, niveaux de pollution, et même les emplacements des personnes. Cependant les appareils de collecte de données ont un espace tampon local limité et la communication de données s’avère coûteuse, il est donc important de pouvoir compresser et renvoyer les données à la volée, ce qui nécessite des algorithmes qui prennent l’enregistrement un par un et construisent le fichier compressé de représentation de la série temporelle pendant la diffusion des données.

Dictée par les données[modifier | modifier le code]

FeaClip[modifier | modifier le code]

Une autre méthode est bien plus utilisée pour la représentation des séries temporelles et chronologiques. Il s’agit de la méthode d'extraction de caractéristiques de la représentation clipping, appelée FeaClip pour les données de représentation et de compression. Grâce à FeaClip, les données aberrantes peuvent être rapidement et automatiquement détectés. Elle utilise les algorithmes des k-médoïdes, utilisé généralement pour le regroupement non aberrant des représentations FeaClip. Selon beaucoup de sources, FeaClip a montré qu’il pouvait effectuer des calculs « haute performance ».

D’un autre côté, son désavantage est le temps de calcul de compression des séries : ce temps est souvent causé par le temps d’extraction.

FeaTrend et FeaClipTrend[modifier | modifier le code]

Le k-échantillon test d'Anderson-Darling a été adapté pour une détection de changement de flux de séries chronologiques agrégées. Le code source de FeaTrend est une méthode de création et de visualisation de la représentation FeaClip.

L’avantage est de pouvoir analyser le comportement et prédire la performance des prévisions.

Cependant, FeaClip et FeaClipTrend ont de meilleures performances de calculs, notamment pour la classification des données avant compression, lorsque le flux de données est trop important.

Basées sur un modèle[modifier | modifier le code]

Modèle additif généralisé (GAM)[modifier | modifier le code]

Le Modèles Additifs Généralisés (GAM) permet de représenter les séries temporelles en utilisant un modèle additif du paramètre naturel de lois de la famille exponentielle (Poisson, Binomial, Gamma, Gauss…).

Cette méthode permet l’extension à des variables non gaussiennes grâce à cette formule :

$g[\mu {}]=\theta =S_{1}(X_{1})+S_{2}(X_{2})$

D’après la plupart des sources, le principale avantage de cette méthode est la simplicité de lecture des informations. En revanche, toujours selon ces mêmes sources, cette méthode manque de précision selon les données compressées.

Exponential smoothing seasonal[modifier | modifier le code]

L’exponential Smoothing Seasonal (lissage exponentielle tendance et saisonniers) permet de prévoir la série saisonnière avec les tendances à la hausse ou à la baisse en utilisant l'algorithme de lissage exponentiel de Holt-Winters. Deux techniques de désaisonnalisation sont disponibles : additif et multiplicatif.

Additif

Soit les observations $X_{1},X_{2},...,X_{t}$ d’une série temporelle, l'algorithme de saisonnalité dit « Holt-Winters additif » calcule une équation de tendance évoluant avec un réglage saisonnier qui est additif.

Additif signifie que la quantité de l'ajustement est constant pour tous les niveaux (valeur moyenne) de la série. L'algorithme de prévision utilise les formules suivantes :

$a_{t}=\alpha {}(X_{t}-F_{t-s})+(1-\alpha {})(a_{t-1}+b_{t-1})$

$b_{t}=\beta (a_{t}-a_{t-1})+(1-\beta {})b_{t-1}$

$F_{t}=\gamma {}(X_{t}-a_{t})+(1-\gamma {})F_{t-s}$

Où $\alpha$ , $\beta$ , et $\gamma$ sont des constantes de lissage entre zéro et un. De plus, une $a_{t}$ donne l'ordonnée à l'origine au moment $t$ , tandis que $b_{t}$ est la pente à l'instant $t$ . La lettre s représente le nombre de périodes par année, de sorte que les données trimestrielles soient représentées par $s=4$ et les données mensuelles par $s=12$ . Les prévisions au moment $T$ pour la valeur à l'instant $T+k$ sont ABK.

Multiplicatif

Soit les observations $X_{1},X_{2},...,X_{t}$ d’une série chronologique, l'algorithme de saisonnalité dit « Holt-Winters multiplicatif » calcule une équation de tendance en évolution avec un ajustement saisonnier qui est multiplicatif.

Ce terme « multiplicatif » signifie que la quantité de l'ajustement varie avec le niveau (valeur moyenne) de la série. De plus, la nature de la plupart des séries temporelles économiques rendent le modèle multiplicatif plus populaire que le modèle additif. L'algorithme de prévision utilise les formules suivantes :

$a_{t}=\alpha {}(X_{t}/F_{t-s})+(1-\alpha {})(a_{t-1}+b_{t-1})$

$b_{t}=\beta (a_{t}-a_{t-1})+(1-\beta {})b_{t-1}$

$F_{t}=\gamma {}(X_{t}/a_{t})+(1-\gamma {})F_{t-s}$

Cette méthode présentation a de nombreux avantages :

D’abord, elle est facile à appliquer, seules trois données sont nécessaires pour les méthodes de lissage exponentiel, nous avons besoin :

Des prévisions pour la période la plus récente
De la valeur réelle pour cette période
De la valeur de la constante de lissage, un facteur de pondération qui reflète le poids attribué aux valeurs de données les plus récentes.

De plus, il produit des prévisions précises. Une méthode de lissage exponentiel produit une prévision pour une période à venir. En utilisant la technique de projection de tendance, il est alors possible de générer des prévisions pour plusieurs périodes. La prévision est considérée comme exacte car elle explique la différence entre les projections réelles et ce qui s'est réellement passé.

Enfin, elle permet de mettre en avant les observations récentes. Celle-ci sont la somme de deux composants ou plus, l’une étant l’erreur aléatoire qui est la différence entre la valeur observée et la vraie valeur. En général, dans une technique de lissage, la variation aléatoire est négligée. Il est alors beaucoup plus facile de voir le phénomène sous-jacent.

En revanche, l’utilisation de cette méthode a quelques inconvénients :

Cette méthode de présentation produit des prévisions en retard sur la tendance actuelle. Le décalage est un effet secondaire du processus de lissage. De ce fait, elle néglige les hauts et les bas associés aux variations aléatoires. En réalité, si l’on l’observe le graphique, on constatera qu’une courbe ou une ligne est plus lisse.

Les tendances sont mal gérées car le lissage exponentiel est mieux utilisé pour les prévisions à court terme et en l'absence de variations saisonnières ou cycliques. Par conséquent, les prévisions ne sont pas précises que lorsque des données présentant des variations cycliques ou saisonnières sont présentes. Pour conclure, ce type de calcul de la moyenne ne fonctionnera pas bien s'il y a une tendance dans la série.

Similairement, pour l’utilisation de cette méthode, il vaut avoir des prévisions à court terme car elle suppose que les tendances futures ressembleront aux tendances actuelles. De ce fait, bien que ce type d’hypothèse puisse sembler raisonnable à court terme, il crée des problèmes au fur et à mesure que les prévisions avancent. Des méthodes comme celle-ci ne sont précises que si l'on peut supposer une continuité raisonnable entre le passé et l'avenir.

En revanche, il existe des variations de lissage exponentiel permettant de gérer les tendances, comme la méthode de Holt. Cette méthode permet de calculer des tendances fortes alors que celle de Winter peut couvrir une tendance forte et des variations saisonnières.

Récapitulatif[modifier | modifier le code]

Dans le tableau ci-dessous, les avantages et désavantages de chacune des représentations des séries temporelles sont récapitulés. Les noms anglais et les noms français s'y retrouvent aussi confinés ainsi que leur nom de fonction équivalente dans le package R TSrepr.

Tableau Récapitulatif des Représentations des séries temporelles
Nom anglais de la représentation	Nom français de la représentation	Fonction R	Avantages de la représentation	Désavantages de la représenatation
DCT - Discrete Cosine Transform	Transformée en cosinus discrète	repr_dct(x,coef=10)	Coefficients toujours réels. Exprimer la DCT en fonction de la DFT . Pas de fuite spectrale. Énergie plus concentrée que la DFT. Bon compresseur sur de petits intervalles.	Les fonctions de la base sont très longues. Basses fréquences précises mais hautes fréquences peu précises. Perte de la non stationnarité sur de grands intervalles.
DFT – Discrete Fourier Transform	Transformée de Fourier discrète	repr_dft(x,coef=10)	Périodicité. Linéarité. Conservation de l’énergie (Parseval). Complexité en mémoire et en temps faible. Facile à comprendre et intuitif. Peu filtrer les éléments non stationnaire.	Pas un très bon compresseur de séries temporelles.
DWT – Discrete Wavelet Transform	Transformée en ondelettes discrète	repr_dwt(x, level=4, filter=’d4’)	Même formalisme que Fourier mais sur une base différente. Peut être une compression sans perte. Les bases orthogonales entraînement des calcul rapide.	Peut être une compression avec perte
PAA – Piecewise Aggregate Approximation	Approximation d’agrégats par morceaux	repr_paa(x, q, func)	Réduction de la dimensionnalité. Tendance globale conservée. Modèle de base pour les méthodes d’agrégations.	Tendance locale perdue. Ne conserve que certaines caractéristiques.
PIP – Perceptually Important Points	Points perceptuellement importants	repr_pip(x, times = 10, return = "points")	Réduction du nombre de dimensions. Conservation des principales caractéristiques. Permet de construit des motifs (détectables par grammaire ou modèle)
SMA - Simple Moving Average	Moyenne mobile simple	repr_sma(x, order)	Facilité de calcul Pas beaucoup de données du passé Suppression automatique après une certaine période Facile à comprendre	La prévision des résultats dépend de la longueur de la moyenne : nécessite le calcul de la prévision Coût élevé en sauvegarde car nécessite de conserver des données du passé. Les données ont tous la même importance La prévision des tendance est moyenne
SAX – Symbolic Aggregate Approximation	Approximation d’agrégat symbolique	repr_sax(x, q = 2, a = 6, eps = 0.01)	Efficace en temps de calcul. Épisode de même taille. Même set de symbole au fil des épisodes.	Erreur de modélisation très importante car le modèle n’est pas localement adapté aux données. Les classes d’équivalence ne sont pas pertinentes pour les mêmes raisons.
PLA – PieceWise Linear Approximation	Approximation linéaire par morceaux	repr_pla(x, times = 10, return = "points")	Solution au problème classique de compression depuis 1960. Utilisé pour la télétransmission des données. Peut être utilisé comme compresseur au fur et à mesure. Concision en mémoire.
GAM regression coeficients as representation	Modèle additif généralisé	repr_gam(x, freq = NULL, xreg = NULL)	Simplicité de lecture des informations	Manque de précision selon le type et la quantité de données traitées
Exponential smoothing seasonal	Lissage exponentiel saisonniers	repr_exp(x, freq, alpha = TRUE, gamma = TRUE)	Facilité d’application : dépend 3 paramètres. Prévisions précises : technique de projection« tendance » Mise en avant des récentes observations les plus importantes	Prévisions en retard Prévisions pas précises lorsque des données présentant des variations cycliques ou saisonnières sont présentes. Nécessite des prévisions à court terme Pas précise si pas de supposition d’une continuité raisonnable entre le passé et l'avenir.
FeaClip – Feature extraction from clipped representation	Extraction de caractéristiques à partir d’une représentation découpée	repr_feaclip(x)	Rapidité et automatisation de détection de données aberrantes Calcul de « haute performance »	Temps de calcul de compression des séries
FeaClipTrend – Feature extraction from clipped end trending representation	Extraction de caractéristiques à partir de la représentation découpée et des tendances	repr_feacliptrend(x, func, pieces = 2L, order = 4L)	Pouvoir analyser le comportement et prédire la performance des prévisions	FeaClip a de meilleures performances de calcul lorsque le flux de données est trop important.
FeaTrend – Feature extraction from clipped representation	Extraction d’entités à partir de la représentation des tendances	repr_featrend(x, func, pieces = 2L, order = 4L)

Conclusion[modifier | modifier le code]

Après avoir défini les différentes notions et terminologies afin de nous familiariser avec le sujet, notre étude comparative nous a permis d'arriver à la conclusion suivante :

La meilleure représentation des séries temporelles est la représentation basée sur les points perceptuellement importants (PIP).

Cette représentation réduit considérablement l'espace image du signal, car elle réduit le bruit mais pas les informations importantes. Une fois que ces bruits sont réduits on peut compresser le signal d'une façon optimale. PIP est donc un bon outil pour la compression des séries temporelles.

PIP permet de construire des motifs détectables par une grammaire formelle ou un modèle, cette propriété peut être utilisée pour entraîner des systèmes experts.

La majorité des caractéristiques usuellement employées sont conservées par cette représentation, c'est donc un point important puisque cette compression peut être considérée comme étant sans pertes. Cette propriété confère un avantage important vis à vis des autres représentations temporelles comparées.

Sources[modifier | modifier le code]

[1] De Livera, A. Hyndman, R., & Snyder, R. (2010). Forecasting time series with complex seasonal patterns using exponential smoothing. Monash University, Department of Econometrics and Business Statistics. Working paper 15/09.

[2] Billah, M., Hyndman, R., & Koehler, A. (2003). Empirical information criteria for time series forecasting model selection. Monash University, Faculty of Business and Economics, Department of Econometrics and Business Statistics, Working Papers.

[3] Gould, P., Koehler, A., Ord, J., Snyder R., Hyndman, R., & Vahid-Araghi, F. (2008). Forecasting time series with multiple seasonal patterns. European Journal of Operational Research, Volume 191, Issue 1, pp. 207-222.

[4] Rasmussen, R. (2004).On time series data and optimal parameters. Omega, Volume 32, Issue 2, pp. 111-120.

[5] Sanjoy, k . (2011). Determination of Exponential Smoothing Constant to Minimize Mean Square Error and Mean Absolute Deviation. Global Journal of Research in Engineering, Volume 11, Issue 3, pp. 31-34.50

[6] Ostertagova, E., & Ostertag, O. (2012). Forecasting using simple exponential smoothing method. Acta Electrotechnica et Informatica, Vol. 12, No. 3, pp. 62-66.

[7] Andrawis, R., & Atiya, A. (2009). A New Bayesian Formulation for Holt’s Exponential Smoothing. Journal of Forecasting, 28, pp. 218-234.

[8] Ho Kim, M., Lee, S., & Chang Lee, K. (2008). Predictive Hybrid Redundancy using Exponential Smoothing Method for Safety Critical Systems. International Journal of Control, Automation, and Systems, vol. 6, no. 1, pp. 126-134.

[9] Sbrana, G. (2012).Damped trend exponential smoothing: prediction and control. Journal of Quantitative Economics, Vol. 10, No.2, pp. 152-159.

[10] Cipra, T., & Hanzak, T. (2008). Exponential smoothing for irregular time series. Kybernetika, Volume 44, Number 3, pp. 385-399.

[11] Shaolin, H., Wei, Z., Li Ye & Shunxi, F. (2011). Adaptive Outlier-tolerant Exponential Smoothing Prediction Algorithms with Applications to Predict the Temperature in Spacecraft. (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 2, No. 11, pp. 130-133.

[12] R. Agrawal, C. Faloutsos, and A. Swami. Efficient Similarity Search in Sequence Databases. In proceedings of FODO, 1993.

[13] N. Ahmed, T. Natarajan, and K. R. Rao. Discrete Cosine Transform. In IEEE Transactions on Computers, 1974.

[14] C. Antunes and A. Oliveira. Temporal data mining: an overview. In proceedings of Workshop on Temporal Data Mining, 2001.

[15] I. Batal, L. Sacchi, R. Bellazzi, and M. Hauskrecht. Multivariate Time Series Classification with Temporal Abstractions. In proceedings of FLAIRS, 2009.

[16] S. Burrus, R. Gopinath, and G. Guo. Introduction to Wavelets and Wavelet Transform. Prentice-Hall, Englewood Cliffs, N. J., 1997.

[17] K. Chan and A. Fu. Efficient Time Series Matching by Wavelets. In proceedings of ICDE, 1999.

[18] C. Faloutsos. Searching Multimedia Databases by Content. Kluwer Academic Publishers, Norwell, MA, first edition, 1996.

[19] D. L. Gall. MPEG: A Video Compression Standard for Multimedia Applications. Communications of the ACM, 34(4):46–58, 1991.

[20] E. Keogh and S. Kasetty. On the need for time series data mining benchmarks: a survey and empirical demonstration. In proceedings of ACM SIGKDD, 2002.

[21] R. E. Kirk. Experimental Design: Procedures for the Behavioral Sciences. Brooks/Cole, Pacific Grove, CA, third edition, 1995.

[22] S. Laxman and P. Sastry. A survey of temporal data mining. SADHANA, Academy Proceedings in Engineering Sciences, 31:173–198, 2006.

[23] O. Mangasarian and D. Musicant. Lagrangian Support Vector Machines. Journal of Machine Learning Research, 2001.

[24] A. Oppenheim and R. Schafer. Digital Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, 1975.

[25] V. Vapnik. The Nature of Statistical Learning Theory. Springer-Verlag, NY, 1995.

[26] V. Vapnik. Statistical Learning Theory. Wiley-Interscience, 1998.

[27] M. Vlachos, J. Lin, E. Keogh, and D. Gunopulos. A Wavelet-Based Anytime Algorithm for K-Means Clustering of Time Series. In proceedings of SIAM International Conference on Data Mining, 2003.

[28] G. Wallace. The JPEG Still Picture Compression Standard. Communications of the ACM, 34(4):30–44, 1991.

[29] Fisher, W. D. (1958). On grouping for maximum homogeneity. Jasa (53), 789–798.

[30] Hugueney, B. (2003). ”Représentations symboliques de longues séries temporelles”. Ph. D. thesis, LIP6.

[31] Keogh, E., K. Chakrabarti, M. Pazzani, and S. Mehrotra (2001a). Locally adaptive dimensionality reduction for indexing large time series databases. SIGMOD Record (ACM Special Interest Group on Management of Data) 30 (2), 151–162.

[32] Keogh, E. and M. J. Pazanni (1998). An enhanced representation of time series which allows fast and accurate classification, clustering and relevance feedback. In D. Heckerman, H. Mannila, D. Pregibon, and R. Uthurusamy (Eds.), Proceedings of the Forth International Conference on Knowledge Discovery and Data Mining (KDD-98). AAAI Press.

[33] Keogh, E. J., K. Chakrabarti, M. J. Pazzani, and S. Mehrotra (2001b). Dimensionality reduction for fast similarity search in large time series databases. Knowledge and Information Systems 3 (3), 263–286.

[34] Lechevallier, Y. (1990). Recherche d’une partition optimale sous contrainte d’ordre total. Technical report, INRIA.

[35] Lin, J., E. Keogh, S. Lonardi, and B. Chiu (2003). A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery, pp. 2–11. ACM Press.

[36] Yi, B.-K. and C. Faloutsos (2000). Fast time sequence indexing for arbitrary Lp norms. In A. El Abbadi, M. L. Brodie, S. Chakravarthy, U. Dayal, N. Kamel, G. Schlageter, and K.-Y. Whang (Eds.), VLDB 2000, Proceedings of 26^th International Conference on Very Large Data Bases, September 10–14, 2000, Cairo, Egypt, Los Altos, CA 94022, USA, pp. 385–394. Morgan Kaufmann Publishers.

Cette page est un brouillon appartenant à PCIFRV

Conseils de rédaction

→ N'hésitez pas à publier sur le brouillon un texte inachevé et à le modifier autant que vous le souhaitez.
→ Pour enregistrer vos modifications au brouillon, il est nécessaire de cliquer sur le bouton bleu : « Publier les modifications ». Il n'y a pas d'enregistrement automatique.

Si votre but est de publier un nouvel article, votre brouillon doit respecter les points suivants :

Respectez le droit d'auteur en créant un texte spécialement pour Wikipédia en français (pas de copier-coller venu d'ailleurs).
Indiquez les éléments démontrant la notoriété du sujet (aide).
Liez chaque fait présenté à une source de qualité (quelles sources – comment les insérer).
Utilisez un ton neutre, qui ne soit ni orienté ni publicitaire (aide).
Veillez également à structurer votre article, de manière à ce qu'il soit conforme aux autres pages de l'encyclopédie (structurer – mettre en page).

→ Si ces points sont respectés, pour transformer votre brouillon en article, utilisez le bouton « publier le brouillon » en haut à droite. Votre brouillon sera alors transféré dans l'espace encyclopédique.