Cycle de Carnot

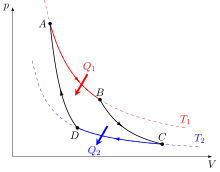
Un article de Wikipédia, l'encyclopédie libre.

Cycle de Carnot dans le diagramme de Clapeyron. AB : détente isotherme ; BC : détente adiabatique ; CD : compression isotherme ; DA : compression adiabatique.

Cycle de Carnot dans le diagramme de entropique. AB : détente isotherme ; BC : détente adiabatique ; CD : compression isotherme ; DA : compression adiabatique.

Le cycle de Carnot est un cycle thermodynamique idéal constituée de quatre processus réversibles : une détente isotherme, une détente adiabatique (isentropique), une compression isotherme, et une compression adiabatique. C'est la méthode la plus efficace pour obtenir du travail à partir de deux sources chaleur de températures constantes ; le cycle inverse est le moyen le plus efficace de transférer de la chaleur d'une source froide à une source chaude à partir d'une source de travail. L'efficacité des autres cycles et des machines réelles est comparé à celui du cycle de Carnot par le biais du rendement, un nombre sans dimension entre 0 (efficacité nulle) et 1 (efficacité du cycle de Carnot).

Il fut publié par Sadi Carnot en 1824 dans son unique ouvrage Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance et permit d'ouvrir la voie à la formulation du second principe de la thermodynamique.

[modifier] Description du cycle

Carnot cherchait à faire un cycle avec la meilleure efficacité^[1] possible. Ainsi chaque efficacité d'une machine thermodynamique peut être comparée avec l'efficacité du cycle de Carnot. Il sert de cycle de référence.

Le cycle est composé de 4 processus ( 2 isothermes et 2 isoentropiques) :

1 : Compression adiabatique réversible
2 : Détente isotherme
3 : Détente adiabatique réversible
4 : Compression isotherme

Le deuxième principe de la thermodynamique permet d'établir pour une transformation réversible (car le fluide est à la température de la source), l'égalité de Clausius-Carnot :

$\frac{Q_f}{T_f}+\frac{Q_c}{T_c}=0$ (notons aussi qu'un moteur thermique necessite deux sources de chaleur, notées ici Qf et Qc ( source froide et source chaude) avec:

$Q f$ transfert thermique avec la source froide (compté négativement).
$Q c$ transfert thermique avec la source chaude (compté positivement).
$T f$ température absolue de la source froide.
$T c$ température absolue de la source chaude.

[modifier] L'efficacité de Carnot

De nombreux systèmes thermodynamiques ont une efficacité définie à partir de celui du Cycle de Carnot, qui est un cycle purement théorique :

$A t o t = A 1,2 + A 2,3 + A 3,4 + A 4,1$ et $Q c =$ chaleurs positives

Donc pour chaque processus :

1-2 :
- $Q 1,2 = 0 = A 1,2 + δ U 1,2$
- d'où : $A_{1,2} = - \delta U_{1,2} = - \frac{i}{2}nR(T_2 - T_1), T_2 > T_1$
2-3 :
- $Q_{2,3} = A_{2,3} = p_2 V_2 \ln\left(\frac{V_3}{V_2}\right)$
- $δ U 2,3 = 0$ car isotherme
3-4 :
- $Q 3,4 = 0 = A 3,4 + δ U 3,4$
- d'où : $A_{3,4} = - \delta U_{3,4} = - \frac{i}{2}nR(T_4 - T_3), T_3 = T_2 = T_c, T_4 = T_1 = T_f$
4-1 :
- $Q_{4,1} = A_{4,1} = p_4 V_4 \ln\left(\frac{V_1}{V_4}\right)$
- $δ U 4,1 = 0$ car isotherme

Donc :

$A_{tot} = nRT_c \ln\left(\frac{V_3}{V_2}\right) + nRT_f \ln\left( \frac{V_1}{V_4} \right)$
$Q_c = nRT_c \ln\left(\frac{V_3}{V_2}\right)$

$\eta = \frac{A_{tot}}{Q_c}=\frac{nRT_c \ln\left(\frac{V_3}{V_2}\right) + nRT_f \ln\left(\frac{V_1}{V_4}\right)}{nRT_c \ln\left(\frac{V_3}{V_2}\right)} = 1 + \frac{T_f}{T_c} \frac{\ln\left(\frac{V_1}{V_4}\right)}{\ln\left(\frac{V_3}{V_2}\right)} = 1 - \frac{T_f}{T_c} \frac{\ln\left(\frac{V_1}{V_4}\right)}{\ln\left(\frac{V_2}{V_3}\right)}$

Mais nous avons l'équation d'état du processus adiabatique : $T \times V^{\gamma -1} = Constante$ d'où :

1-2 : $T_f V_1 ^{\gamma -1} = T_c V_2 ^{\gamma -1}$
3-4 : $T_f V_4 ^{\gamma -1} = T_c V_3 ^{\gamma -1}$

Et donc le rapport : $\frac{T_f V_1 ^{\gamma -1}}{T_f V_4 ^{\gamma -1} } = \frac{T_c V_2 ^{\gamma -1}}{T_c V_3 ^{\gamma -1}}$ donc : $\frac{V_1}{V_4} = \frac{V_2}{V_3}$ et finalement $\ln\left(\frac{V_1}{V_4}\right) = \ln\left(\frac{V_2}{V_3}\right)$

En incorporant ceci dans l'équation de l'efficacité on obtient :

$\eta = 1 - \frac{T_f}{T_c}$ donc pour obtenir une efficacité de 100%, il faut que $\frac{T_f}{T_c}$ soit égal à 0 donc que $T f$ soit égal à 0K soit -273,15°C.

[modifier] Notes et références

↑ L'efficacité thermodynamique est le rapport de ce qui est récupéré sur ce qui a été dépensé. Elle est très souvent confondue avec le rendement qui est le rapport entre l'efficacité réelle et l'efficacité théorique maximale de la machine.