Černá
.svg){kind=icon}
Cet article est une ébauche concernant une localité tchèque.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
| Černá | |
| |
 |
 |
| Administration | |
|---|---|
| Pays |  Tchéquie
|
| Région |  Vysočina
|
| District | Žďár nad Sázavou |
| Région historique | Moravie |
| Maire | Vítězslav Plocek |
| Code postal | 594 42 |
| Indicatif téléphonique international | +(420) |
| Démographie | |
| Population | 296 hab. (2020) |
| Densité | 28 hab./km2 |
| Géographie | |
| Coordonnées | 49° 25′ 34″ nord, 15° 51′ 50″ est |
| Altitude | 523 m |
| Superficie | 1 044 ha = 10,44 km2 |
| Localisation | |
| Liens | |
| Site web | www.obeccerna.cz |
modifier  |
|
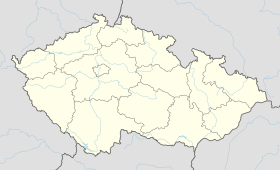
Černá (en allemand : Tscherna) est une commune du district de Žďár nad Sázavou, dans la région de Vysočina, en République tchèque. Sa population s'élevait à 296 habitants en 2020[1].
Géographie[modifier | modifier le code]
Černá se trouve à 14 km au nord-ouest de Velké Meziříčí, à 17 km au sud-sud-ouest de Žďár nad Sázavou, à 21 km à l'est-nord-est de Jihlava à 126 km à l'est-sud-est de Prague[2].
La commune est limitée par Bohdalov et Kyjov au nord, par Pavlov au nord-est, par Zadní Zhořec et Blízkov à l'est, par Měřín et Meziříčko au sud, et par Jersín et Arnolec à l'ouest[3].
Histoire[modifier | modifier le code]
La première mention écrite de la localité date de 1464.
Administration[modifier | modifier le code]
La commune se compose de deux quartiers :
- Černá
- Milíkov
Transports[modifier | modifier le code]
Par la route, Černá se trouve à 14,5 km de Velké Meziříčí, à 20 km de Žďár nad Sázavou, à 23,5 km de Jihlava et à 148 km de Prague[4].
Notes et références[modifier | modifier le code]
- (cs) Population des communes de la République tchèque au 1er janvier 2020.
- Distances à vol d'oiseau ou distances orthodromiques.
- D'après geoportal.gov.cz.
- Selon viamichelin.fr. Distances suivant l'itinéraire le plus court.
