Potentiel de Yukawa
Un potentiel de Yukawa (appelé également 'potentiel de Coulomb écranté') est un potentiel de la forme
Hideki Yukawa montra dans les années 1930 qu'un tel potentiel provient de l'échange d'un champ scalaire massif tel que celui d'un pion de masse . La particule médiatrice du champ possédant une masse, la force correspondante a une portée inversement proportionnelle à sa masse. Pour une masse nulle, le potentiel de Yukawa devient équivalent à un potentiel coulombien, et sa portée est considérée comme infinie.
Dans l'équation ci-dessus, le potentiel est négatif, ce qui indique que la force est attractive. La constante g est un nombre réel; elle est égale à la constante de couplage entre le champ mésonique et le champ fermionique avec lequel il interagit. Dans le cas de la physique nucléaire, les fermions seraient le proton et le neutron.
Obtention du potentiel de Yukawa[modifier | modifier le code]
Partons de l’équation de Klein-Gordon[1]:
Si le second membre est nul, on obtient l'équation des ondes électromagnétiques :
Si, en plus, la fonction d'onde est indépendante du temps, on obtient l'équation du champ électrostatique, c'est-à-dire l'équation de Laplace :
Enfin, en symétrie sphérique fonction de la distance r à la charge ponctuelle, on obtient l'équation de Laplace du champ coulombien :
Le potentiel de Yukawa a la symétrie sphérique et est statique mais garde le second membre. L'équation de Klein-Gordon devient :
où serait la masse du méson ou pion. La solution physiquement acceptable de cette équation différentielle est le potentiel ou V(r) de Yukawa (la fonction d'onde se transforme en potentiel) :
où est la longueur d'onde de Compton. Le potentiel est négatif car il s'agit d'une force de liaison, l'interaction forte, le potentiel d'attraction entre deux nucléons à une distance r. Sa portée, de , rayon du proton, correspond à une masse , celle du méson dont l'existence a été prévue ainsi par Yukawa.
Application du principe d'incertitude[modifier | modifier le code]
On peut faire un calcul approximatif[2]. Le principe d'incertitude d'Heisenberg peut s'écrire:
Supposons que l'incertitude sur le temps soit égale au temps de l'interaction lui-même (on aura ainsi un minimal puisque sera maximal) et calculons . On a:
On trouve une valeur de l'ordre de grandeur attendu.
On obtient exactement le même résultat en utilisant la relation de de Broglie de l'onde de matière appliquée à la longueur d'onde de Compton du proton:
ce qui donne la même approximation de l'énergie du méson:
Transformée de Fourier[modifier | modifier le code]
La façon la plus simple de comprendre que le potentiel de Yukawa est associé à un champ massif consiste à examiner sa transformée de Fourier. On a
où l'intégrale est calculée sur toutes les valeurs possibles du vecteur quantité de mouvement k. Sous cette forme, on peut voir la fraction comme le propagateur ou fonction de Green de l'équation de Klein-Gordon.
Amplitude de Feynman[modifier | modifier le code]
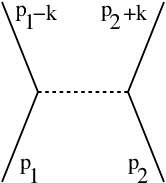
Le potentiel de Yukawa peut être déduit comme amplitude de l'interaction d'une paire de fermions au premier ordre. L'interaction de Yukawa couple le champ fermionique au champ mésonique avec le terme de couplage
L'amplitude de diffusion de deux fermions, l'un avec une quantité de mouvement initiale et l'autre avec une quantité de mouvement , qui échangent un méson de moment k, est donnée par le diagramme de Feynman à droite.
Les règles de Feynman associent pour chaque sommet un facteur multiplicatif g à l'amplitude; ce diagramme ayant deux sommets, l'amplitude totale sera affectée d'un facteur multiplicatif . La ligne médiane qui relie les deux lignes de fermions représente l'échange d'un méson. Selon la règle de Feynman, un échange de particules implique l'utilisation du propagateur; pour un méson massif, ce dernier est . Ainsi, l'amplitude de Feynman pour ce graphe est simplement
À partir de la section précédente, on voit clairement qu'il s'agit de la transformée de Fourier du potentiel de Yukawa.
Références[modifier | modifier le code]
- Escoubès,B, Leite Lopes, J, Sources et évolution de la physique quantique, Textes fondateurs, EDP Sciences,2005
- Foos, J, Manuel de radioactivité à l'usage des utilisateurs,Formascience, Orsay, 1993
- (en) Gerald Edward Brown and A. D. Jackson, The Nucleon-Nucleon Interaction, (1976) North-Holland Publishing, Amsterdam (ISBN 0-7204-0335-9)































