Formule de Weizsäcker
La formule de Weizsäcker, appelée aussi formule de Bethe-Weizsäcker, est une formule semi-empirique donnant une valeur approximative de l'énergie de liaison nucléaire B caractérisant la liaison entre les nucléons qui constituent le noyau des atomes (voir un résumé dans Modèle de la goutte liquide).
Histoire[modifier | modifier le code]
L'éponyme de formule de Weizsäcker[1] est le physicien allemand Carl Friedrich von Weizsäcker (-) qui l'a proposée en [2],[3] dans un article publié dans le Zeitschrift für Physik[4],[5]. Les physiciens Hans Bethe (-) et Robert Bacher (-) en ont simplifié l'expression en [2],[3],[6],[7]. Le physicien Eugene Wigner (-) l'a généralisée en [2],[3],[6],[8]. En , Niels Bohr (-) et John Wheeler (-) y ont introduit le terme [9],[10].
Expression[modifier | modifier le code]
où :
- B est l'énergie de liaison, A est le nombre de masse (ou nombre de nucléons contenus dans le noyau A = Z+N), Z est le nombre de protons ;
- est le terme de volume[11],[12],[13] ;
- est le terme de surface[11],[14],[15] ;
- est le terme coulombien[11],[16],[17] ;
- est le terme d'asymétrie[3],[17],[18],[19] ;
- est le terme de parité[17] ou d'appariement[3],[20].
Remarques :
Dans le terme coulombien, est souvent remplacé par [11],[13],[21] car [22].
Dans certaines formules, le terme d'appariement varie en plutôt qu'en [23].
Les valeurs des constantes utilisées sont (en MeV) :
- av = 15,56
- as = 17,23
- ac = 0,7
- aa = 23,6
- ap = 11,2

Il existe différents jeux de paramètres pour la formule de Weizsäcker. Le choix du jeu de paramètres se définit en fonction des noyaux étudiés. Ainsi certains jeux de paramètres donneront des énergies de liaison plus précises pour les noyaux stables tandis que d'autres jeux donneront des résultats plus satisfaisant pour les noyaux exotiques.
Cette formule permet d'expliquer avec une bonne approximation la courbe d'Aston (ci-contre), qui représente l'énergie de liaison par nucléon en fonction du nombre de nucléons dans le noyau. C'est une courbe expérimentale car chaque énergie de liaison y est calculée à partir de la masse du noyau atomique mesurée par spectrométrie de masse.
Explication des différents termes[modifier | modifier le code]
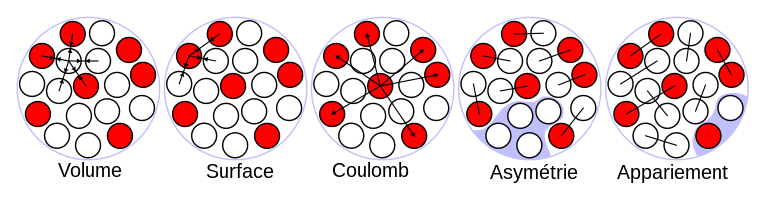
La formule de Bethe-Weizsäcker fait apparaitre cinq termes :
- Les deux premiers sont dus au modèle de la goutte liquide du noyau.
- Le troisième exprime la répulsion électrostatique entre les protons.
- Les deux derniers sont d'ordre quantique.
Pour expliquer ces différents termes, il faut supposer que le noyau est sphérique, de rayon . Et comme il est compact (son volume est proportionnel au nombre de nucléons A), alors est proportionnel à .
Énergie de volume[modifier | modifier le code]
Pour expliquer le premier terme, on peut utiliser une analogie avec un gaz parfait pour lequel l'énergie interne est proportionnelle au nombre de particules constituant le gaz. Ainsi, on pose que cette énergie de volume est proportionnelle à A. Elle permet d'expliquer les forces nucléaires de courtes portées, et la saturation des forces nucléaires :
.
Énergie de surface[modifier | modifier le code]
La notion de tension de surface (ou superficielle) d'une goutte liquide peut être utilisée pour interpréter le second terme. Intuitivement, les nucléons à la surface du noyau sont en contact avec moins de nucléons que ceux du centre, l'énergie de liaison en est donc diminuée, à l'instar (sans que ce soit le même phénomène physique en jeu) de ce qu'il se passe à une interface liquide/gaz telle qu'une goutte d'eau dans l'air.
En introduisant comme le second terme de la formule, on prouve, en première approximation, que la surface du noyau est proportionnelle à .
Pour cela, on approxime que le volume du noyau est proportionnel au nombre de nucléons. Il s'agit d'une approximation courante[24] :
La surface d'une sphère de rayon étant , en remplaçant par son approximation, on obtient :
Répulsion électrostatique[modifier | modifier le code]
Les protons étant tous chargés positivement, ils se repoussent mutuellement. Cela participe à diminuer l'énergie de liaison par un terme de répulsion électrostatique . Dans une approximation grossière, le noyau peut être considéré comme une sphère avec une densité de charge uniforme. L'énergie potentielle d'une telle distribution de charge est donnée par :
où est la charge totale, le rayon de la sphère. En identifiant à et en prenant le rayon proportionnel à , on obtient la forme du terme coulombien. Cependant, la répulsion coulombienne n'existe que lorsqu'il y a plus d'un proton ce qui induit que devient . La valeur de peut être calculée approximativement en utilisant l'équation ci-dessus :
L'énergie potentielle de la distribution de charge est donc :
La constante du terme de répulsion électrostatique est :
Une autre valeur de peut être obtenue en utilisant la constante de structure fine :
où est la constante de structure fine, , le rayon du noyau avec qui vaut approximativement 1,25 femtomètres. Cela donne une valeur théorique de de 0,691 MeV ce qui est peu éloigné des valeurs mesurées.
Énergie d'asymétrie[modifier | modifier le code]
La répulsion électrostatique étant en compétition avec l'interaction forte pour stabiliser le noyau, les noyaux lourds ont besoin d'un surplus de neutrons afin que cette interaction forte contrebalance l'effet de la répulsion électrostatique. Il y a donc une asymétrie du nombre de neutrons par rapport au nombre de protons. Cela n'a, a priori, aucun autre effet sur l'énergie de liaison que ceux qui ont été étudiés plus haut. En réalité, un effet quantique va jouer un rôle : les nucléons se trouvent sur des niveaux d'énergie, ce qui fait qu'un surplus de neutrons va augmenter leur énergie. On obtient alors que l'effet sur l'énergie de liaison s'écrit : .
Énergie d'appariement[modifier | modifier le code]
Un deuxième effet quantique joue un rôle dans l'énergie de liaison : les nucléons ayant un spin demi-entier ont tendance à s'apparier deux à deux, pour se grouper préférentiellement en nombre pair. Ainsi, un nombre impair de neutrons ou de protons sera moins stable.
Une formule empirique permet de rendre compte de cet effet en ajoutant à l'énergie de liaison une énergie d'appariement (ou de parité) ayant différentes valeurs selon qu'il y a un nombre pair ou impair de nucléons, neutrons ou protons :
Les noyaux ayant un nombre pair de nucléons, neutrons et protons sont plus stables que ceux ayant un nombre impair de nucléons, eux-mêmes plus stables que ceux ayant un nombre pair de nucléons et impair de neutrons et protons, donc l'énergie de liaison varie en conséquence.
Utilisation de la formule[modifier | modifier le code]
Équation de la vallée de la stabilité[modifier | modifier le code]
Pour un nombre de masse donné A, on s'aperçoit que la formule de Bethe-Weizsäcker fournit une équation quadratique en fonction de la charge Z. On a ainsi :
Par définition, les noyaux stables sont définis comme étant des noyaux qui maximisent l'énergie de liaison . Ainsi en cherchant les valeurs de qui annulent la dérivée par rapport à , on peut obtenir une équation donnant les noyaux de la vallée de stabilité.
Améliorations[modifier | modifier le code]
De nombreux modèles ont par la suite tenter de raffiner le modèle de la goutte liquide proposé initialement par Carl Friedrich von Weizsäcker en introduisant de nouveaux paramètres afin de reproduire plus finement les masses mesurées expérimentalement.
Modèle de la gouttelette liquide[modifier | modifier le code]
Ce modèle a été proposé par William D. Myers et Wladyslaw J. Swiatecki dans les années 1970. Il ajoute deux paramètres supplémentaires au modèle de la goutte liquide, à savoir la compressibilité de la matière nucléaire et l’asymétrie locale proton-neutron[25].
Modèle de Duflo–Zuker[modifier | modifier le code]
Proposé initialement en 1995 par Jean Duflo et Andres Zuker[26] puis raffiné en 1999[27].
Notes et références[modifier | modifier le code]
- Taillet, Villain et Febvre 2018, s.v.Weizsäcker (formule de), p. 785-786.
- Pfalzner 2006, B.4, p. 217.
- Taillet, Villain et Febvre 2018, s.v.Weizsäcker (formule de), p. 786, col. 1.
- Wapstra 1958, § 15, p. 26, n. 1.
- Weizsäcker 1935.
- Wapstra 1958, § 15, p. 26.
- Bethe et Bacher 1936.
- Wigner 1937.
- Wapstra 1958, § 15, p. 26, n. 3.
- Bohr et Wheeler 1939.
- Le Sech et Ngô 2014, chap. 2, § 2.9, p. 30.
- Mayet 2017, chap. 2, § 2.1, p. 41, 1).
- Reuss 2003, chap. 2, § 2.2.4, p. 49.
- Mayet 2017, chap. 2, § 2.1, p. 42, 2).
- Reuss 2003, chap. 2, § 2.2.4, p. 49-50.
- Mayet 2017, chap. 2, § 2.1, p. 42, 3).
- Reuss 2003, chap. 2, § 2.2.4, p. 50.
- Le Sech et Ngô 2014, chap. 2, § 2.9, p. 30-31.
- Mayet 2017, chap. 2, § 2.1, p. 42-43, 4).
- Mayet 2017, chap. 2, § 2.1, p. 43, 5).
- Taillet, Villain et Febvre 2018, s.v.Weizsäcker (formule de), p. 785, col. 2.
- Khater 2009.
- Le Sech et Ngô 2014, chap. 2, § 2.9, p. 31.
- « Le noyau atomique », sur www.sciences-en-ligne.com (consulté le )
- Guy Royer, Contribution à la description macroscopique des phénomènes nucléaires de fusion, fission et fragmentation (thèse de doctorat en physique nucléaire), (lire en ligne [PDF]), p. 14
- (en) J. Duflo et A.P. Zuker, « Microscopic mass formulas », Physical Review C, vol. 52, , R23 (DOI 10.1103/PhysRevC.52.R23)
- (en) J. Duflo et A.P. Zuker, « Microscopic mass formulas », Physical Review C, vol. 59, , R2347 (DOI 10.1103/PhysRevC.59.R2347)
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
Publications originales[modifier | modifier le code]
- [Weizsäcker 1935] (de) Carl Friedrich von Weizsäcker, « Zur Theorie der Kernmassen » [« Sur la théorie des masses nucléaires »], Zeitschrift für Physik, vol. 96, nos 7-8, , p. 431-458 (OCLC 5653580744, DOI 10.1007/BF01337700, Bibcode 1935ZPhy...96..431W).
- [Bethe et Bacher 1936] (en) Hans A. Bethe et Robert F. Bacher, « Nuclear physics : A. – Stationary states of nuclei » [« Physique nucléaire : A. – États stationnaires des noyaux »], Reviews of Modern Physics, vol. 8, no 2, , p. 82-229 (OCLC 4643731788, DOI 10.1103/RevModPhys.8.82, Bibcode 1936RvMP....8...82B, lire en ligne [PDF]).
- [Wigner 1937] (en) Eugene Wigner, « On the structure of nuclei beyond oxygen » [« Sur la structure des noyaux au-delà de l'oxygène »], Physical Review, vol. 51, no 11, , p. 947-958 (OCLC 4644011967, DOI 10.1103/PhysRev.51.947, Bibcode 1937PhRv...51..947W, résumé).
- [Bohr et Wheeler 1939] (en) Niels Bohr et John Archibald Wheeler, « The mechanism of nuclear fission » [« Le mécanisme de fission nucléaire »], Physical Review, vol. 56, no 5, , p. 426-450 (OCLC 4644057022, DOI 10.1103/PhysRev.56.426, Bibcode 1939PhRv...56..426B, résumé, lire en ligne [PDF]).
Manuels d'enseignement supérieur[modifier | modifier le code]
- [Basdevant 2016] Jean-Louis Basdevant, La physique quantique et ses applications, Paris, Vuibert, coll. « LMD / Physique », , 1re éd., 1 vol., IX-421, ill., fig. et graph., 17 × 24 cm (ISBN 978-2-311-40039-7, EAN 9782311400397, OCLC 957581835, BNF 44272737, SUDOC 194834077, présentation en ligne, lire en ligne), § 5.2.2 (« La formule de masse de Bethe-Weizsäcker »), p. 102-105.
- [Basdevant, Rich et Spiro 2002] Jean-Louis Basdevant, James Rich et Michel Spiro, Énergie nucléaire, Palaiseau, École polytechnique, hors coll., (réimpr. ), 1 vol., 336, ill., 17 × 24 cm (ISBN 978-2-7302-0901-4, EAN 9782730209014, OCLC 64768914, BNF 38862997, SUDOC 069243158, présentation en ligne, lire en ligne), § 2.2 (« La formule de masse de Bethe-Weizsäcker »), p. 67-71.
- [Le Sech et Ngô 2014] Claude Le Sech et Christian Ngô, Physique nucléaire : des quarks aux applications, Paris, Dunod, coll. « Sciences Sup / Physique », , 2e éd. (1re éd. ), 1 vol., XVI-271, ill., 24 cm (ISBN 978-2-10-070541-2, EAN 9782100705412, OCLC 881576971, BNF 43822194, SUDOC 178846775, présentation en ligne, lire en ligne), § 2.9 (« Le modèle de la goutte liquide »), p. 29-31.

- [Pfalzner 2006] (en) Susanne Pfalzner, An introduction to inertial confinement fusion [« Une introduction à la fusion nucléaire par confinement inertiel »], New York et Londres, Taylor & Francis, coll. « Series in plasma physics », (réimpr. ), 1re éd., 1 vol., 232, ill., 16 × 24 cm (ISBN 978-0-7503-0701-7 et 978-0-3673-9109-6, EAN 9780750307017, OCLC 62679899, BNF 41099603, DOI 10.1201/9781420011845, SUDOC 112896030, présentation en ligne, lire en ligne), B.4 (« Constants of the semiempirical mass formula ») [« Constantes de la formule semi-empirique de masse »], p. 217.

- [Reuss 2003] Paul Reuss, Précis de neutronique, Les Ulis, EDP Sciences et INSTN, coll. « Génie atomique », (réimpr. ), 1re éd., 1 vol., 533, ill., fig. et graph., 17 × 24 cm (ISBN 2-86883-637-2, EAN 9782868836373, OCLC 470236789, BNF 39042390, SUDOC 074172719, présentation en ligne, lire en ligne), § 2.2.4 (« Modèle de goutte »), p. 49-51.

Dictionnaires et encyclopédies[modifier | modifier le code]
- [Taillet, Villain et Febvre 2018] Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Supérieur, hors coll., , 4e éd. (1re éd. ), 1 vol., X-956, ill., fig. et graph., 17 × 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, BNF 45646901, SUDOC 224228161, présentation en ligne, lire en ligne), s.v.Weizsäcker (formule de), p. 785-786.

- [Wapstra 1958] (de + en) Aaldert Hendrik Wapstra, « Atomic masses of nuclides », dans Siegfried Flügge (éd.), Handbuch der Physik / Encyclopedia of physics [« Encyclopedie de physique »], t. XXXVIII, 1re part. : Äussere Eigenschaften der Atomkerne / External properties of atomic nuclei [« Propriétés externes des noyaux atomiques »], Berlin, Göttingen et Heidelberg, Springer, coll. « Kernphysik / Nuclear physics » (no 8 / 38 / 1), (réimpr. ), 1re éd., 1 vol., VI-471, ill., fig. et graph., 17 × 24,4 cm (ISBN 978-3-642-45902-3, OCLC 467895019, BNF 37353867, DOI 10.1007/978-3-642-45901-6, SUDOC 015349322, présentation en ligne, lire en ligne), chap. 1er [« Masses atomiques des nucléides »], p. 1-37 (OCLC 7322443398, DOI 10.1007/978-3-642-45901-6_1).

Articles connexes[modifier | modifier le code]
Liens externes[modifier | modifier le code]
- [Khater 2009] Antoine Khater, « Introduction à la physique nucléaire », dans Ressources numériques pédagogiques pour la licence physique, (lire en ligne), § 2.10 (« Relation empirique pour l'énergie de liaison par nucléon ») (lire en ligne).

- [Valentin n.d.] Luc Valentin, « Nucléaire (physique) : noyau atomique », dans Encyclopædia Universalis, n.d. (lire en ligne), § 2 (« Masse et énergie de liaison ») (lire en ligne).


















































