Conjecture 1/3 - 2/3

Un article de Wikipédia, l'encyclopédie libre.
(Redirigé depuis Conjecture 1/3-2/3)
Un ordre partiel formé à partir d'un ordre série-parallèle (en). Parmi les 27 ordres totaux le prolongeant, l'élément en bas à gauche est supérieur à l'élément en bas à droite dans 9 cas ; des ordres partiels ayant cette structure sont les seuls cas connus pour lesquels la conjecture 1/3–2/3 correspond à la borne exacte.

En théorie des ordres, en combinatoire et en algorithmique, la conjecture 1/3–2/3 affirme que lors d'un tri par comparaison, quelles que soient les comparaisons déjà effectuées, il est toujours possible de choisir la comparaison suivante de telle sorte que le nombre d'ordres possibles soit réduit d'un facteur au moins égal à 2/3 et au plus à 1/3. Cela est équivalent à ce que dans tout ensemble partiellement ordonné fini non totalement ordonné, il existe deux éléments x et y tels qu'au moins 1/3 et au plus 2/3 des extensions linéaires de l'ordre partiel placent x avant y.

Définitions et énoncé de la conjecture[modifier | modifier le code]

Un ensemble partiellement ordonné est un ensemble X muni d'une relation binaire ≤ réflexive, antisymétrique, et transitive. Un ordre total est un ordre partiel pour lequel tout couple d'éléments est comparable. Un ordre total sur X prolonge l'ordre partiel si x ≤ y pour l'ordre partiel entraîne x ≤ y pour l'ordre total. Sauf si X est totalement ordonné, plusieurs prolongements sont possibles, et la conjecture 1/3–2/3 affirme qu'il existe alors toujours deux éléments x et y (non comparables) tels que parmi ces prolongements, x est avant y dans au moins 1/3 des cas (et donc, par symétrie, y est avant x dans au plus 2/3 des cas)[1].

Dans le langage de la théorie des probabilités, on peut formuler la conjecture ainsi : avec une distribution de probablilité uniforme sur les ordres totaux prolongeant l'ordre donné, il existe toujours deux éléments x et y tels que la probabilité que x soit avant y dans une de ces extensions choisie au hasard est comprise entre 1/3 and 2/3 (en revanche, la conjecture ne dit rien sur la probabilité qu'il en soit ainsi si x et y sont choisis au hasard)[1].

En 1984, Jeff Kahn et Michael Saks ont défini δ(P), pour un ordre partiel P, comme le plus grand réel δ tel que P admette un couple (x, y) avec x précédant y dans une proportion d'ordres totaux prolongeant P comprise entre δ et 1−δ. Avec cette notation, la conjecture 1/3–2/3 affirme que les ordres partiels finis vérifient δ(P) ≥ 1/3[2].

Exemples[modifier | modifier le code]

L'ordre partiel formé par trois éléments a, b, et c avec la seule relation a ≤ b a trois prolongements totalement ordonnés : a ≤ b ≤ c, a ≤ c ≤ b, et c ≤ a ≤ b. a précède c dans deux de ces ordres, et donc le couple (a,c) possède la propriété cherchée, ce qui montre que cet ordre partiel vérifie la conjecture 1/3–2/3 (et que ces nombres sont les meilleurs possibles)[3].

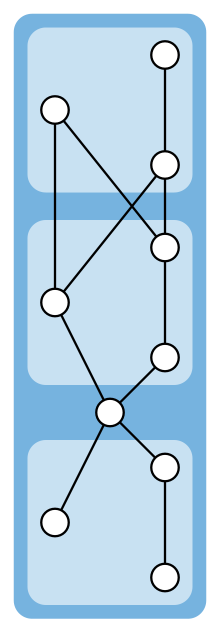
Plus généralement, soit P un ordre série-parallèle (en) composé à partir d'ordres partiels, comme sur la figure ci-contre. P est un cas extrémal de la conjecture1/3–2/3, au sens où pour chaque paire d'éléments non comparables, l'un des deux apparait avant l'autre dans au plus 1/3 des ordres totaux prolongeant P. Les ordres construits ainsi sont les seuls cas extrémaux connus de la conjecture, et on peut démontrer que ce sont les seuls cas extrémaux d'ordres partiels de largeur 2[4].

Historique[modifier | modifier le code]

La conjecture 1/3–2/3 fut formulée par Sergey Kislitsyn (en) en 1968[5], et indépendamment par Michael Fredman (en)[6] et par Nati Linial en 1984[1]. Elle figurait comme exemple de conjecture ouverte dans le premier numéro de la revue Order, et reste non résolue ; elle a été appelée « l'un des problèmes les plus intrigants de la théorie des ensembles partiellement ordonnés[1] ». Un tour d'horizon de l'état de la conjecture a été publié en 1999[7].

Résultats partiels[modifier | modifier le code]

La conjecture 1/3–2/3 est vérifiée par certaines classes d'ordre partiels, comme ceux de largeur 2[8], ceux de hauteur 2[9], ceux ayant au plus 11 éléments[10], ceux dans lesquels chaque élément est incomparable à au plus 6 autres[11], ou encore les polyarbres[12]. La proportion d'ordres partiels à n éléments pour lesquels la conjecture est vraie tend vers 100% lorsque n tend vers l'infini[10].

En 1995, Graham Brightwell, Stefan Felsner, et William Trotter démontrèrent que pour tout ordre P (non total), δ(P) ≥ 1/2 − √5/10 ≈ 0.276, améliorant plusieurs autres bornes antérieures[13]. Utilisant l'interprétation probabiliste de δ(P) pour le définir pour des ordres infinis, ils montrèrent que cette borne est optimale, car il existe des ordres infinis pour lesquels δ(P) = 1/2 − √5/10.

Applications[modifier | modifier le code]

En 1984, Jeff Kahn et Michael Saks proposèrent l'application suivante : on veut trier par comparaison un ensemble X totalement ordonné, pour lequel on a déjà certaines information sous forme d'un ordre partiel. La conjecture 1/3–2/3 affirme qu'à chaque étape il existe une comparaison qui réduit d'un facteur 2/3 (dans le plus mauvais cas) le nombre d'ordres compatibles avec l'information déjà connue, ce qui implique que s'il restait initialement un nombre E d'ordres possibles, le tri demande au plus log3/2E comparaisons[2].

Cette analyse néglige cependant la difficulté de sélectionner la paire optimale pour chaque nouvelle comparaison. De plus, on peut parfois trier avec un nombre de comparaisons inférieur à ce que suggère cette analyse, le plus mauvais cas ne se produisant pas forcément à chaque étape. En fait, il est conjecturé que logφE comparaisons peuvent suffire,, où φ est le nombre d'or[10].

Généralisations et résultats associés[modifier | modifier le code]

En 1984, Kahn et Saks ont également conjecturé que, lorsque w tend vers l'infini, la valeur de δ(P) pour des ensembles partiellement ordonnés de largeur w devrait tendre vers 1/2. En particulier, ils s'attendent à ce que seuls des ordres de largeur 2 correspondent au pire cas δ(P) = 1/3[14], et en 1985 Martin Aigner a énoncé cela comme une c conjecture explicite[4]. La plus petite valeur connue de δ(P) pour des ordres de largeur 3 est 14/39[15], et on sait qu'on ne peut avoir une valeur inférieure pour des ordres de largeur 3 ayant 9 éléments ou moins[9]. Une autre conjecture basée également sur des explorations par ordinateur est que si δ(P) ne vaut pas exactement 1/3, alors δ(P) ≥ 0.348843[16].

Marcin Peczarski a formulé une « conjecture de la partition dorée » affirmant que pour tout ordre non total, on peut trouver deux comparaisons successives telles que, notant ti le nombre d'ordres totaux compatibles avec ce qui reste après que i des comparisons aient été faites, alors (quel que soit le résultat de ces comparaisons) t0 ≥ t1 + t2. Cette conjecture implique la conjecture 1/3–2/3, et implique également (avec les notations précédentes) que le tri peut s'effectuer avec au plus logφE comparaisons, d'où le nom de cette conjecture en relation avec le nombre d'or[10],[11].

Notes[modifier | modifier le code]

  1. ↑ a b c et d Brightwell, Felsner et Trotter (1995).
  2. ↑ a et b Kahn et Saks 1984
  3. ↑ Kahn et Saks 1984 ; Brightwell, Felsner et Trotter 1995.
  4. ↑ a et b Aigner (1985).
  5. ↑ Kislitsyn 1968
  6. ↑ Fredman 1976. Cependant, en dépit de la relation étroite des questions qu'il analyse avec la conjecture 1/3–2/3, celle-ci n'est pas mentionnée explicitement dans cet article.
  7. ↑ Brightwell 1999
  8. ↑ Linial 1984, Theorem 2; Sah 2021.
  9. ↑ a et b Trotter, Gehrlein et Fishburn (1992).
  10. ↑ a b c et d Peczarski 2006.
  11. ↑ a et b Peczarski 2008.
  12. ↑ Zaguia (2019).
  13. ↑ Brightwell, Felsner et Trotter 1995; Kahn et Saks 1984; Khachiyan 1989; Kahn et Linial 1991; Felsner et Trotter 1993.
  14. ↑ Kahn et Saks (1984).
  15. ↑ Saks (1985).
  16. ↑ Peczarski (2019).

Références[modifier | modifier le code]


Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Conjecture_1/3_-_2/3&oldid=210166256 ».