Angles alternes-internes

Un article de Wikipédia, l'encyclopédie libre.

En géométrie, deux droites coupées par une sécante forment des angles dont les sommets sont aux points d'intersection.

Sommaire 1 Définition 2 Droites quelconques 3 Droites parallèles 4 Voir aussi

[modifier] Définition

Deux angles formés par deux droites coupées par une sécante sont dits angles alternes-internes si :

1. ils sont situés de part et d'autre de la sécante ;
2. ils sont situés à l'intérieur des deux droites ;
3. ils ne sont pas adjacents.

[modifier] Droites quelconques

Les droites (xx') et (yy') sont coupées respectivement en A et en B par la sécante (tt').

et sont des angles alternes-internes.

[modifier] Droites parallèles

Propriété

• Si deux droites parallèles sont coupées par une sécante, alors ces droites forment des angles alternes-internes égaux.
• Réciproquement, si deux droites coupées par une sécante forment des angles alternes-internes égaux, alors ces deux droites sont parallèles.

Sur la figure ci-dessus, les droites a et b sont parallèles et s est une sécante à ces deux droites.

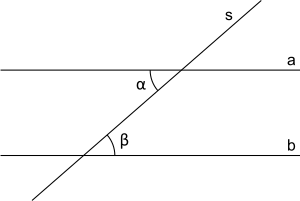α et β sont des "Angles égaux"

[modifier] Voir aussi

v · d · m Différents angles remarquables
Aigu • Droit • Obtus • Plat • Rentrant • Plein Adjacents • Opposés par le sommet • Correspondants • Alternes-internes • Alternes-externes Complémentaires • Supplémentaires D'or

• Portail de la géométrie