Aller au contenu

« Graphe sommet-connexe » : différence entre les versions

Un article de Wikipédia, l'encyclopédie libre.
Navigation interactive dans l’historique
← Modification précédenteModification suivante →
Contenu supprimé Contenu ajouté
VisuelWikicode
Vers75 (discuter | contributions)
16 135 modifications
m →‎Exemples : + Lien
ManiacParisien (discuter | contributions)
20 080 modifications
m Un peu étoffé
Ligne 1 : Ligne 1 :
{{ébauche|mathématiques}}
{{ébauche|mathématiques}}
[[File:4-connected graph.svg|thumb|Un graphe 4-sommet-connexe.]]
⚫
En [[théorie des graphes]], un [[graphe non orienté|graphe connexe]] {{Citation|est dit ''k''-'''sommet-connexe''' s'il possède au moins ''k'' + 1 sommets et s'il reste encore connexe après en avoir ôté ''k'' – 1<ref>{{harvsp|Matoušek|Nešetřil|p=144}}.</ref>}}.


== Définitions ==
⚫
En [[théorie des graphes]], un [[graphe non orienté|'''graphe''' connexe]] {{Citation|est dit ''k''-'''sommet-connexe''' s'il possède au moins ''k'' + 1 sommets et s'il reste encore connexe après en avoir ôté ''k'' – 1<ref>{{Ouvrage|titre=Introduction aux mathématiques discrètes|auteur=[[Jiří Matoušek]]|auteur2=[[Jaroslav Nešetřil]]|éditeur=[[Springer Science & Business Media|Springer]]|année=2004|url={{Google Livres|NZlcnzvTxAwC|page=144}}|page=144}}.</ref>.}}


Un graphe autre qu'un [[graphe complet]]) est de degré de ''sommet-connexité'' ''k'' s'il est ''k''-sommet-connexe sans être ''k+1''-sommet-connexe, donc si ''k'' est la taille du plus petit sous-ensemble de sommets dont la suppression disconnecte le graphe<ref name="Schrijver">{{harvsp|Schrijver|2003|p=}}.</ref>. Les graphes complets ne sont pas inclus dans cette version de la définition car ils ne peuvent pas être déconnectés en supprimant des sommets. Le graphe complet à ''n'' sommets est de degré de connexité ''n-1''.
⚫
Un [[graphe régulier]] de degré ''k'' est au plus ''k''-sommet-connexe et ''k''-[[Graphe arête-connexe|arête-connexe]]. S'il est effectivement ''k''-sommet-connexe et ''k''-arête-connexe, il est dit optimalement connecté.

Une définition équivalente est qu'un graphe avec au moins deux sommets est ''k''-sommet-connexe, pour chaque paire de ses sommets, il existe est ''k'' [[Chaîne (théorie des graphes)|Chaîne]]s indépendantes reliant ces sommets ; c'est le [[théorème de Menger]]<ref>{{Harvsp|Diestel|2016}}.</ref>. Cette définition produit la même réponse ''n''&nbsp;&minus;&nbsp;1, pour la connexité du graphe complet ''K''<sub>''n''</sub><ref name="Schrijver"/>.

Un graphe 1-sommet-connexe est un appelé un [[graphe connexe]] ; un graphe 2-sommet-connexe et appelé un [[graphe biconnexe]]. Un graphe 3-connexe est aussi appelé triconnexe.

⚫
Un [[graphe régulier]] de degré ''k'' est au plus ''k''-sommet-connexe et ''k''-[[Graphe arête-connexe|arête-connexe]]. S'il est effectivement ''k''-sommet-connexe et ''k''-arête-connexe, il est dit ''optimalement connecté''.


== Exemples ==
== Exemples ==
Ligne 9 : Ligne 17 :
*Pour tout ''k'' > 2 et tout ''j'' > 1, le [[graphe moulin]] Wd(''k'', ''j'') est 1-sommet-connexe. Pour le séparer en ''j'' composantes connexes, il suffit de supprimer son sommet de plus haut degré : son centre.
*Pour tout ''k'' > 2 et tout ''j'' > 1, le [[graphe moulin]] Wd(''k'', ''j'') est 1-sommet-connexe. Pour le séparer en ''j'' composantes connexes, il suffit de supprimer son sommet de plus haut degré : son centre.
*Le [[graphe cycle]] C<sub>n</sub> est 2-sommet-connexe pour tout ''n'' > 3.
*Le [[graphe cycle]] C<sub>n</sub> est 2-sommet-connexe pour tout ''n'' > 3.
*Le [[110-graphe de Iofinova-Ivanov]] est 3-sommet-connexe
*Le [[110-graphe de Iofinova-Ivanov]] est 3-sommet-connexe.


<gallery>
<gallery>
Image:Biggs-Smith graph.svg|Le [[graphe de Biggs-Smith]] est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
Image:Biggs-Smith graph.svg|Le [[graphe de Biggs-Smith]] est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
Image:Windmill graph Wd(5,4).svg|Le graphe moulin Wd(5,4) devient déconnecté si l'on supprime son sommet central. Il est 1-sommet-connexe.
Image:Windmill graph Wd(5,4).svg|Le [[graphe moulin]] Wd(5,4) n'est plus connexe si l'on supprime son sommet central: il est 1-sommet-connexe.
Image:Complete graph K6.svg|Le [[graphe complet]] K<sub>6</sub> est 5-sommet-connexe.
Image:Complete graph K6.svg|Le [[graphe complet]] K<sub>6</sub> est 5-sommet-connexe.
</gallery>
</gallery>

== Nombre de graphes selon leur sommet-connexité ==

Nombre de graphes simples <math>k</math>-sommet-connexes à <math>n</math> sommets pour <math>n</math> de 1 à 9, avec la référence à [[On-Line Encyclopedia of Integer Sequences|OEIS]] :

:{| class="wikitable"
|-
! <math>k</math> \ <math>n</math> !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 !! 9 !! OEIS
|-
! scope="row" | total
| 1 || 2 || 4 || 11 || 34 || 156 || 1044 || 12346 || 274668 || [[OEIS:A000088|A000088]]
|-
! scope="row" | 1
| 1 || 1 || 2 || 6 || 21 || 112 || 853 || 11117 || 261080 || [[OEIS:A001349|A001349]]
|-
! scope="row" | 2
| 0 || 1 || 1 || 3 || 10 || 56 || 468 || 7123 || 194066 || [[OEIS:A002218|A002218]]
|-
! scope="row" | 3
| 0 || 0 || 1 || 1 || 3 || 17 || 136 || 2388 || 80890 || [[OEIS:A006290|A006290]]
|-
! scope="row" | 4
| 0 || 0 || 0 || 1 || 1 || 4 || 25 || 384 || 14480 || [[OEIS:A086216|A086216]]
|-
! scope="row" | 5
| 0 || 0 || 0 || 0 || 1 || 1 || 4 || 39 || 1051 || [[OEIS:A086217|A086217]]
|-
! scope="row" | 6
| 0 || 0 || 0 || 0 || 0 || 1 || 1 || 5 || 59 ||
|-
! scope="row" | 7
| 0 || 0 || 0 || 0 || 0 || 0 || 1 || 1 || 5 ||
|}

Nombre de graphes simples exactement <math>k</math>-sommet-connexes à <math>n</math> sommets:

:{| class="wikitable"
|-
! <math>k</math> \ <math>n</math> !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7 !! 8 !! 9 !! OEIS
|-
! scope="row" | 0
| 0 || 1 || 2 || 5 || 13 || 44 || 191 || 1229 || 13588 ||
|-
! scope="row" | 1
| 1 || 0 || 1 || 3 || 11 || 56 || 385 || 3994 || 67014 || [[OEIS:A052442|A052442]]
|-
! scope="row" | 2
| 0 || 1 || 0 || 2 || 7 || 39 || 332 || 4735 || 113176 || [[OEIS:A052443|A052443]]
|-
! scope="row" | 3
| 0 || 0 || 1 || 0 || 2 || 13 || 111 || 2004 || 66410 || [[OEIS:A052444|A052444]]
|-
! scope="row" | 4
| 0 || 0 || 0 || 1 || 0 || 3 || 21 || 345 || 13429 || [[OEIS:A052445|A052445]]
|-
! scope="row" | 5
| 0 || 0 || 0 || 0 || 1 || 0 || 3 || 34 || 992 ||
|-
! scope="row" | 6
| 0 || 0 || 0 || 0 || 0 || 1 || 0 || 4 || 54 ||
|}


== Référence ==
== Référence ==
{{Références}}
{{Références}}


== Bibliographie ==
* {{Ouvrage|titre=Introduction aux mathématiques discrètes|auteur=[[Jiří Matoušek]]|auteur2=[[Jaroslav Nešetřil]]|éditeur=[[Springer Science & Business Media|Springer]]|année=2004|url={{Google Livres|NZlcnzvTxAwC|page=144}}}}
* {{ouvrage | auteur1=Reinhard Diestel | titre=Graph Theory | éditeur=Springer-Verlag
| date=2016| collection = Graduate Texts in Mathematics, Volume 173
| isbn=978-3-662-53621-6 |isbn2=978-3-96134-005-7|pages totales = 447|numéro édition = 5
|url=http://diestel-graph-theory.com/basic.html? }}
* {{Ouvrage
|auteur1= Lutz Volkmann
|titre= Fundamente der Graphentheorie
|éditeur= Springer
|année= 1996
|pages totales=
|url= http://www.math2.rwth-aachen.de/files/gt/buch/graphen_an_allen_ecken_und_kanten.pdf
|isbn= 3-211-82774-9
|consulté le=11 février 2021
}}.
* {{ouvrage | auteur1=[[Alexander Schrijver]] | titre=Combinatorial optimization |sous-titre = Polyhedra and efficiency
| éditeur=Springer| Ort=Berlin| date=2003| isbn=978-3-540-44389-6 | pages totales = 1881 (3 volumes)}}

== Liens externes ==
* {{MathWorld|nom_url=k-ConnectedGraph|titre= k-Connected Graph}}
== Article connexe ==
== Article connexe ==
* [[Graphe arête-connexe]]
[[Lexique de la théorie des graphes]]
* [[Lexique de la théorie des graphes]]


{{portail|géométrie|informatique théorique}}
{{portail|géométrie|informatique théorique}}

Version du 11 février 2021 à 12:28

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

Un graphe 4-sommet-connexe.

En théorie des graphes, un graphe connexe « est dit k-sommet-connexe s'il possède au moins k + 1 sommets et s'il reste encore connexe après en avoir ôté k – 1[1] ».

Définitions

Un graphe autre qu'un graphe complet) est de degré de sommet-connexité k s'il est k-sommet-connexe sans être k+1-sommet-connexe, donc si k est la taille du plus petit sous-ensemble de sommets dont la suppression disconnecte le graphe[2]. Les graphes complets ne sont pas inclus dans cette version de la définition car ils ne peuvent pas être déconnectés en supprimant des sommets. Le graphe complet à n sommets est de degré de connexité n-1.

Une définition équivalente est qu'un graphe avec au moins deux sommets est k-sommet-connexe, pour chaque paire de ses sommets, il existe est k Chaînes indépendantes reliant ces sommets  ; c'est le théorème de Menger[3]. Cette définition produit la même réponse n − 1, pour la connexité du graphe complet Kn[2].

Un graphe 1-sommet-connexe est un appelé un graphe connexe ; un graphe 2-sommet-connexe et appelé un graphe biconnexe. Un graphe 3-connexe est aussi appelé triconnexe.

Un graphe régulier de degré k est au plus k-sommet-connexe et k-arête-connexe. S'il est effectivement k-sommet-connexe et k-arête-connexe, il est dit optimalement connecté.

Exemples

  • Pour tout n, le graphe complet Kn (régulier de degré n – 1) est optimalement connecté.
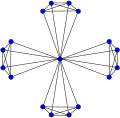
  • Pour tout k > 2 et tout j > 1, le graphe moulin Wd(k, j) est 1-sommet-connexe. Pour le séparer en j composantes connexes, il suffit de supprimer son sommet de plus haut degré : son centre.
  • Le graphe cycle Cn est 2-sommet-connexe pour tout n > 3.
  • Le 110-graphe de Iofinova-Ivanov est 3-sommet-connexe.
  • Le graphe de Biggs-Smith est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
    Le graphe de Biggs-Smith est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
  • Le graphe moulin Wd(5,4) n'est plus connexe si l'on supprime son sommet central: il est 1-sommet-connexe.
    Le graphe moulin Wd(5,4) n'est plus connexe si l'on supprime son sommet central: il est 1-sommet-connexe.
  • Le graphe complet K6 est 5-sommet-connexe.
    Le graphe complet K6 est 5-sommet-connexe.

Nombre de graphes selon leur sommet-connexité

Nombre de graphes simples -sommet-connexes à sommets pour de 1 à 9, avec la référence à OEIS :

\ 1 2 3 4 5 6 7 8 9 OEIS
total 1 2 4 11 34 156 1044 12346 274668 A000088
1 1 1 2 6 21 112 853 11117 261080 A001349
2 0 1 1 3 10 56 468 7123 194066 A002218
3 0 0 1 1 3 17 136 2388 80890 A006290
4 0 0 0 1 1 4 25 384 14480 A086216
5 0 0 0 0 1 1 4 39 1051 A086217
6 0 0 0 0 0 1 1 5 59
7 0 0 0 0 0 0 1 1 5

Nombre de graphes simples exactement -sommet-connexes à sommets:

\ 1 2 3 4 5 6 7 8 9 OEIS
0 0 1 2 5 13 44 191 1229 13588
1 1 0 1 3 11 56 385 3994 67014 A052442
2 0 1 0 2 7 39 332 4735 113176 A052443
3 0 0 1 0 2 13 111 2004 66410 A052444
4 0 0 0 1 0 3 21 345 13429 A052445
5 0 0 0 0 1 0 3 34 992
6 0 0 0 0 0 1 0 4 54

Référence

  1. ↑ Matoušek Nešetřil, p. 144.
  2. ↑ a et b Schrijver 2003.
  3. ↑ Diestel 2016.

Bibliographie

Liens externes

Article connexe

Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Graphe_sommet-connexe&oldid=179800989 ».