Graphe arête-connexe
En théorie des graphes, un graphe k-arête-connexe est un graphe connexe qu'il est possible de déconnecter en supprimant k arêtes et tel que ce k soit minimal. Il existe donc un ou plusieurs ensembles de k arêtes dont la suppression rende le graphe déconnecté, mais la suppression de k-1 arêtes, quelles qu'elles soient, le fait demeurer connexe.
Un graphe régulier de degré k est au plus k-arête-connexe et k-sommet-connexe. S'il est effectivement k-arête-connexe et k-sommet-connexe, il est qualifié de graphe optimalement connecté.
Exemples[modifier | modifier le code]
- Pour tout n, le graphe complet Kn est optimalement connecté. Il est (n-1)-sommet-connexe, (n-1)-arête-connexe et (n-1)-régulier.
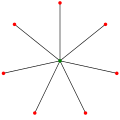
- Le graphe biparti complet K(1,n) est 1-arête-connexe pour tout n.
- Le graphe cycle Cn est 2-arête-connexe pour tout n>2.
- Le 110-graphe de Iofinova-Ivanov est 3-arête-connexe.
- Un graphe 2-arête-connexe est un graphe connexe sans isthme.
-
Le graphe de Gray est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
-
Le graphe complet K5 est 4-arête-connexe.
-
Le graphe biparti complet K(1,7) est 1-arête-connexe.