Arbre bicolore

Un arbre bicolore ou arbre rouge et noir est un type particulier d'arbre binaire de recherche équilibré, qui est une structure de données utilisée en informatique théorique. Les arbres bicolores ont été inventés en 1972 par Rudolf Bayer qui les nomme symmetric binary B-trees (littéralement « arbres B binaires symétriques »). Leur principal intérêt réside dans la complexité logarithmique en le nombre d'éléments des opérations suivantes : l'insertion, la recherche et la suppression. Ils sont cependant assez complexes à mettre en œuvre, car les opérations d'insertion et de suppression font appel à de nombreuses études de cas. Enfin, ils sont isomorphes aux arbres 2-3-4.

Utilisation et avantages

Les arbres bicolores, ainsi que les arbres AVL, offrent la meilleure garantie sur le temps d'insertion, de suppression et de recherche dans les cas défavorables. Ceci leur permet non seulement d'être alors utilisables dans des applications en temps réel, mais aussi de servir comme fondement d'autres structures de données à temps d'exécution garanti dans les cas défavorables, par exemple en géométrie algorithmique.

Propriétés

Exemple d'arbre bicolore. La hauteur noire de cet arbre est de 2.

Un arbre bicolore est un arbre binaire de recherche dans lequel chaque nœud a un attribut supplémentaire : sa couleur, qui est soit rouge soit noire. En plus des restrictions imposées aux arbres binaires de recherche, les règles suivantes sont utilisées :

1. Un nœud est soit rouge soit noir ;
2. La racine est noire ;
3. Le parent d'un nœud rouge est noir ;
4. Tous les nœuds ont 2 enfants. Ils peuvent être d'autres nœuds, où des feuilles NIL qui ne possède pas de valeur, et qui sont les seuls nœuds sans enfants. Leur couleur est toujours noire et rentre donc en compte lors du calcul de la hauteur noire.
5. Le chemin de la racine à n'importe quelle feuille (NIL) contient le même nombre de nœuds noirs. On peut appeler ce nombre de nœuds noirs la hauteur noire. Lors du calcul, on ne compte pas le 1^er nœud.

Ces contraintes impliquent une propriété importante des arbres bicolores : le chemin le plus long possible d'une racine à une feuille (sa hauteur) ne peut être que deux fois plus long que le plus petit possible. Un arbre est ainsi presque équilibré. Comme les opérations d'insertion, de recherche et de suppression requièrent dans le pire des cas un temps proportionnel à la hauteur de l'arbre, les arbres bicolores restent efficaces, contrairement aux arbres binaires de recherche ordinaires.

Pour comprendre comment ces contraintes garantissent la propriété ci-dessus, il suffit de s'apercevoir qu'aucun chemin ne peut avoir deux nœuds rouges consécutifs à cause de la propriété 3. Le plus petit chemin théorique de la racine à une feuille ne contient alors que des nœuds noirs tandis que le plus grand alterne entre les nœuds rouges et noirs. Et comme d'après la propriété 4, chacun de ces chemins contient le même nombre de nœuds noirs, le plus grand chemin ne peut être deux fois plus grand que le plus petit.

La propriété 2 n'est pas nécessaire. Les seuls cas où la racine pourrait devenir rouge étant les deux cas où sa couleur n'a pas d'importance : soit la racine est le seul nœud, soit elle possède deux fils noirs. Cette propriété est ajoutée uniquement pour visualiser plus rapidement l'isomorphisme avec les arbres 2-3-4 : chaque nœud noir et ses éventuels fils rouges représente un nœud d'arbre 2-3-4.

Opérations

La recherche sur un arbre bicolore s'effectue exactement comme dans les arbres binaires de recherche. Cependant, après une insertion ou une suppression, les propriétés de l'arbre bicolore peuvent être violées. La restauration de ces propriétés requiert un petit nombre ($O(\log(n))$) de modifications des couleurs (qui sont très rapides en pratique) et pas plus de trois rotations (deux pour l'insertion). Ceci permet d'avoir une insertion et une suppression en $O(\log(n))$ mais complique grandement les opérations à cause du grand nombre de cas à étudier.

Insertion

Implémentation en C

struct node *insertion(struct noeud *racine, struct noeud *n)
 {
   // Insertion d'un nouveau noeud dans l'arbre
   insertion_recursif(racine, n);

   // Réparation de l'arbre au cas où les propriétés rouge-noir seraient violées
   insertion_repare_arbre(n);

   // Recherche de la nouvelle racine à renvoyer
   racine = n;
   
   while (parent(racine) != NULL)
      racine = parent(racine);
    
   return n;
 }

void insertion_recursif(struct noeud *racine, struct noeud *n)
 {
   // Descente récursive dans l'arbre jusqu'à atteindre une feuille
   if (racine != NULL && n->clé < racine->clé) {
      if (racine->gauche != FEUILLE) {
         insertion_recursif(racine->gauche, n);
         return;
	  }
      else
         racine->gauche = n;
   } else if (racine != NULL) {
      if (racine->droit != FEUILLE) {
         insertion_recursif(racine->droit, n);
         return;
	  }
      else
         racine->droit = n;
   }

   // Insertion du nouveau noeud n
   n->parent = racine;
   n->gauche = FEUILLE;
   n->droit = FEUILLE;
   n->couleur = ROUGE;
 }

void insertion_repare_arbre(struct noeud *n)
 {
   if (parent(n) == NULL)
      insertion_cas1(n);
   else if (parent(n)->couleur == NOIR)
      insertion_cas2(n);
   else if (oncle(n)->couleur == ROUGE)
      insertion_cas3(n);
   else
      insertion_cas4(n);
 }

void insertion_cas1(struct noeud *n)
 {
   if (parent(n) == NULL)
      n->couleur = NOIR;
 }

void insertion_cas2(struct noeud *n)
 {
   return; /* Ne rien faire puisque l'arbre est bien un arbre rouge-noir */
 }

Diagramme du cas 3

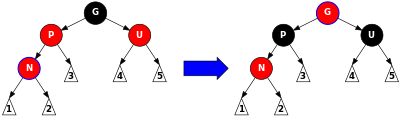
void insertion_cas3(struct noeud *n)
 {
   parent(n)->couleur = NOIR;
   oncle(n)->couleur = NOIR;
   
   struct noeud *g = grandparent(n);
   g->couleur = ROUGE;
   insertion_repare_arbre(g);
 }

Diagramme du cas 4

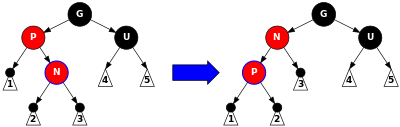
void insertion_cas4(struct noeud *n)
 {
   struct noeud *p = parent(n);
   struct noeud *g = grandparent(n);

   if (n == g->gauche->droit) {
      rotation_gauche(p);
      n = n->gauche;
   } else if (n == g->droit->gauche) {
      rotation_droit(p);
      n = n->droit; 
   }

   insertion_cas4etape2(n);
 }

Suite du cas 4

void insertion_cas4etape2(struct node *n)
 {
   struct noeud *p = parent(n);
   struct noeud *g = grandparent(n);

   if (n == p->gauche)
      rotation_droit(g);
   else
      rotation_gauche(g);
  
   p->couleur = NOIR;
   g->couleur = ROUGE;
 }

Suppression

La suppression commence par une recherche du nœud à supprimer. Si le nœud supprimé est rouge, les propriétés restent satisfaites. Si le nœud supprimé est noir, on perd la propriété 4, l'arbre doit alors être réorganisé en remontant jusqu'à la racine.