Morphologie mathématique

La morphologie mathématique est une théorie et technique mathématique et informatique d'analyse de structures qui est liée avec l'algèbre, la théorie des treillis, la topologie et les probabilités.
Le développement de la morphologie mathématique est inspiré des problèmes de traitement d'images, domaine qui constitue son principal champ d'application. Elle fournit en particulier des outils de filtrage, segmentation, quantification et modélisation d'images. Elle est également utilisable en traitement du signal, par exemple pour filtrer les variations d'une mesure (physique, biologique) au cours du temps.
Aperçu général[modifier | modifier le code]
Une des idées de base de la morphologie mathématique est d'étudier ou de traiter un ensemble à l'aide d'un autre ensemble, appelé élément structurant, qui sert de sonde. À chaque position de l'élément structurant, on regarde s'il touche ou s'il est inclus dans l'ensemble initial. En fonction de la réponse, on construit un ensemble de sortie. On obtient ainsi des opérateurs de base qui sont relativement intuitifs.
Des propriétés que l'on retrouve souvent dans les opérateurs morphologiques sont :
- la non-linéarité ;
- la non-inversibilité ;
- l'idempotence.
Ceci implique en particulier une perte d'information ; bien utilisés, ces opérateurs permettent d'éliminer des structures ne respectant pas certains critères, comme de largeur ou de volume.
La morphologie mathématique s'intéresse aussi aux ensembles et aux fonctions aléatoires.
Le principal domaine d'application de la morphologie mathématique est le traitement d'images. Elle fournit, en particulier, des outils de filtrage, de segmentation et de quantification. Depuis son apparition, en 1964, elle connaît un succès grandissant et désormais contribue à garnir la boite à outils de tout traiteur d'images.
Bref historique[modifier | modifier le code]
La morphologie mathématique a été inventée en 1964 par Georges Matheron et Jean Serra dans les laboratoires de l'école des Mines de Paris. Son développement a toujours été fortement motivé par des applications industrielles. Dans un premier temps, il s'est agi de répondre à des problèmes dans le domaine de l'exploitation minière, mais très vite ses champs d'applications se sont diversifiés : biologie, imagerie médicale, sciences des matériaux, vision industrielle, multimédia, télédétection et géophysique constituent quelques exemples de domaines dans lesquels la morphologie mathématique a apporté une contribution importante.
La morphologie mathématique reste un domaine actif de recherche. En témoignent les nombreuses publications scientifiques sur le sujet, ainsi que les symposiums internationaux sur la morphologie mathématique qui ont lieu tous les deux ou trois ans.
Quelques exemples de thèmes de recherche actuels :
- ligne de partage des eaux : parallélisation, approche topologique, hiérarchisation ;
- extension à des espaces non-euclidiens, à des fonctions vectorielles (images en couleurs, images multi-spectrales, etc.) et à des images non conventionnelles;
- liens avec l'apprentissage profond (réseaux morphologiques; pré-traitement et post-traitement);
- approches stochastiques pour la segmentation et le filtrage;
- architectures électroniques efficaces pour l'implantation d'opérateurs morphologiques;
- développement d'algorithmes rapides;
- traitement de nuages de points;
- modélisation de structures physiques, en particulier dans le domaine des sciences des matériaux.
Opérateurs de base[modifier | modifier le code]
La morphologie mathématique peut être développée dans le cadre abstrait de la théorie des treillis. Cependant, une présentation plus pratique, visant un utilisateur potentiel d'outils de traitement d'images, plutôt qu'un mathématicien, est ici adoptée.
Cas ensembliste[modifier | modifier le code]
Plaçons-nous dans , souvent utilisé comme modélisation du support des images binaires à deux dimensions, même si tout ce qui est présenté dans cette section reste valable dans , où est un entier strictement positif. Soit un sous-ensemble de , appelé élément structurant. Si est un élément de , alors nous noterons l'ensemble translaté de :
L'élément structurant joue en quelque sorte le rôle de modèle local, ou de sonde. Il est promené partout sur l'image à traiter, et à chaque position on étudie sa relation avec l'image binaire, considérée comme un ensemble. Ces relations peuvent être du type « est inclus dans l'ensemble », ou « touche l'ensemble », par exemple.
En pavage carré, les éléments structurants les plus classiquement utilisés sont la croix, constituée de l'origine et des quatre points les plus proches, et le carré, constitué de l'origine et des huit points les plus proches. Ces deux éléments structurants correspondent respectivement à deux définitions possibles du voisinage d'un pixel ou du type de connexité de l'image. En pavage hexagonal, l'élément de base est l'hexagone centré.
On introduit aussi le symétrique d'un ensemble, noté :
Si est symétrique, on a .
Dilatation et érosion[modifier | modifier le code]
Soit un sous-ensemble de . La dilatation morphologique avec l'élément structurant est définie comme la somme de Minkowski[1]:
Une autre formulation plus intuitive est :
La dilatation morphologique n'est, en général, pas inversible. L'opération qui en quelque sorte tente de produire l'inverse de la dilatation est l'érosion morphologique:
La dilatation et l'érosion sont les opérateurs de base de la morphologie mathématique. Pratiquement tous les autres peuvent être définis à l'aide de ceux-ci, en utilisant des compositions de fonctions et des opérations ensemblistes.
-
Image originale (en noir : l'objet ; en blanc : le fond).
-
Dilatation par un carré 3x3 : les pixels noirs et gris font partie de l'ensemble résultant.
-
Érosion par un carré 3x3 : seuls les pixels noirs font partie de l'ensemble résultant.
Propriétés algébriques de la dilatation et de l’érosion[modifier | modifier le code]
La dilatation est une transformation extensive si B contient l’origine : L’érosion est anti-extensive si B contient l'origine : La dilatation et l’érosion sont des transformations croissantes (comme l’union et l’intersection) : La dilatation et l’érosion ne sont pas des transformations idempotentes : Par contre la dilatation et l’érosion vérifient la propriété d’itérativité qui permet de construire des dilatations ou des érosions avec des éléments structurants homothétiques : La dilatation est une transformation continue et l’érosion est une transformation semi-continue supérieure. Cette propriété découle directement de la propriété de l’intersection dans la soustraction de Minkowski.
La dilatation est distributive par rapport à l’union et l’érosion par rapport à l’intersection : Soit une famille d’éléments structurants homothétiques et une homothétie de rapport . La compatibilité de la dilatation et de l’érosion avec les homothéties s’écrivent :
Propriétés topologiques de la dilatation et de l'érosion[modifier | modifier le code]
La dilatation, comme l’union, préserve la connexité. La dilatation n’est pas une transformation qui préserve l’homotopie. En effet, elle connecte des éléments disjoints et bouche des trous. L’érosion n’est pas une transformation qui préserve l’homotopie. En effet, elle sépare les parties connexes et supprime des éléments lorsqu’ils sont petits. L’érosion, comme l’intersection, ne préserve pas la connexité.
Ouverture et fermeture[modifier | modifier le code]
La composition d'une dilatation morphologique avec l'érosion par le même élément structurant ne produit pas, en général, l'identité, mais deux autres opérateurs morphologiques, l'ouverture morphologique : et la fermeture morphologique : L'ouverture peut être caractérisée géométriquement: elle donne l'union de tous les inclus dans . Ainsi, la forme de l'élément structurant permet de choisir les structures qui peuvent le contenir.
La fermeture est le dual de l'ouverture : la fermeture du complémentaire d'un ensemble est égale au complémentaire de l'ouverture de cet ensemble.
On notera que si l'élément structurant n'est pas symétrique, on devra utiliser l'élément symétrique pour le second opérateur (dilatation dans le cas de l'ouverture et érosion dans le cas de la fermeture).
Propriétés de l’ouverture et de la fermeture[modifier | modifier le code]
- La fermeture et l'ouverture sont des opérations croissantes et idempotentes, deux propriétés qui définissent les filtres morphologiques.
- La fermeture est extensive (), et l'ouverture est anti-extensive ().
- L’ouverture et la fermeture sont des opérateurs semi-continu supérieur. C’est l’érosion qui impose cette propriété, la dilatation étant continue.
- Du point de vue topologique, l’ouverture ne préserve pas la connexité alors que la fermeture la préserve. L’ouverture et la fermeture ne sont pas des transformations homotopiques.
-
Image originale
-
Fermeture par un carré 3×3 : les pixels noirs et gris font partie de l'ensemble résultant
-
Ouverture par un carré 3×3 : seuls les pixels noirs font partie de l'ensemble résultant
Transformation en tout ou rien[modifier | modifier le code]
On peut aussi prendre deux éléments structurants et pour définir des transformations. Si on demande en chaque point à d'être à l'extérieur de l'ensemble et à à l'intérieur on obtient la transformation en tout ou rien (hit or miss transform en anglais) : où désigne le complémentaire de l'ensemble . Cette transformation permet de détecter certaines configurations précises de pixels. Parmi les configurations les plus utilisées on aura :
- Les points extrêmes et les points triples du squelette obtenu par amincissement.
- Les configurations correspondant aux différents nombres de connexités.
Épaississement et amincissement[modifier | modifier le code]
En ajoutant le résultat de la transformation à l'ensemble initial on obtient un épaississement : en enlevant le résultat de l'ensemble initial on obtient un amincissement :
Applications : squelette, skiz, enveloppe convexe[modifier | modifier le code]
- En prenant des suites d'amincissements, on peut réduire progressivement l'ensemble initial (comme si on l'épluchait). De cette façon on peut calculer différents types de squelettes, dont des squelettes homotopiques.
- Des épaississements homotopiques permettent aussi de construire des Skiz (squelettes par zone d’influence).
- Avec une autre configuration on pourra obtenir par épaississement les enveloppes convexes.
Extension aux fonctions[modifier | modifier le code]
Une image à niveaux de gris peut être modélisée comme une fonction de dans . Soit une fonction appartenant à cet ensemble. On a alors :
L'ouverture et la fermeture de fonctions s'obtiennent comme dans le cas ensembliste :
L'ouverture et la fermeture morphologiques constituent déjà des outils intéressants de filtrage d'images. Cependant, ils peuvent modifier le contour des objets, propriété qui peut être malvenue. Les opérateurs par reconstruction et plus généralement les nivellements, introduits plus loin, permettent de pallier cet inconvénient.
Épaississements et amincissements ne sont pas, en général, des opérateurs croissants. Par conséquent, leur application aux fonctions (en pratique, aux images à niveaux de gris) n'est pas triviale. Plusieurs extensions ont été proposées dans la littérature.
Exemple d'utilisation : détection de contours[modifier | modifier le code]
La détection de contours représente une tâche importante en traitement d'images. La morphologie mathématique propose des outils non-linéaires de détection de contours, comme le gradient et le laplacien morphologiques.
Le gradient morphologique, aussi appelé gradient de Beucher du nom de son inventeur, est défini par :
Il correspond, en quelque sorte, à la version morphologique du module du gradient euclidien.
Le laplacien morphologique est construit de façon analogue :
où correspond à l'opérateur identité.
Opérateurs connexes, nivellements[modifier | modifier le code]
Tous les opérateurs définis dans les sections précédentes l’ont été dans un cadre euclidien à savoir que l’espace de définition de l’image sert de référence pour les opérateurs. Dans cette section, on va reprendre les deux opérateurs de base que sont l’érosion et la dilatation mais en restant dans un sous espace de , nommé espace de référence. Les transformations euclidiennes deviendront ainsi des transformations géodésiques (appelées aussi transformations conditionnelles).
La géodésie est la science de la mesure de la forme et des dimensions de la terre. Ainsi une distance géodésique correspond au chemin le plus court pour aller d’un point à un autre en restant à la surface du globe. La longueur de ce chemin, à la différence de la distance euclidienne, ne correspond pas à un segment droit mais à celle d’un arc géodésique. La définition d’arc géodésique implique la notion de connexité par arc. Un espace topologique est dit connexe par arcs si tout couple de points de est relié par un chemin dont le support est inclus dans .
De l’euclidien au géodésique pour les ensembles[modifier | modifier le code]
Distance euclidienne et distance géodésique[modifier | modifier le code]
La distance géodésique utilise les mêmes axiomes que la distance euclidienne, seul, le chemin est différent.
Soit quatre points .
Sur la partie gauche de l’image, on a représenté les segments de droite associés aux différentes distances euclidiennes. Sur la partie droite, on a représenté les trois arcs géodésiques reliant et . On remarque que le point ne possède aucun chemin géodésique car il appartient à une composante disjointe de celle contenant les trois autres points.

La distance géodésique vérifie bien les axiomes d’une distance. On a, en effet :
À ces axiomes, il faut ajouter un quatrième. Lorsqu'il n’y a aucun chemin géodésique, on a :Pour les mêmes points, il est possible de comparer les distances géodésiques par rapport à et les distances euclidiennes. On aura toujours une distance géodésique plus grande ou égale à la distance euclidienne avec la possibilité d’avoir une distance euclidienne finie et une distance géodésique infinie :On notera au passage que, pour relier deux points, il peut y avoir plusieurs arcs géodésiques équivalents, alors que le chemin euclidien est unique.
Élément structurant géodésique[modifier | modifier le code]
Dans l’élément structurant isotrope centré en et de taille est le disque fermé , défini par :Le disque géodésique, se définit par rapport à l’ensemble de référence en remplaçant la distance euclidienne par la distance géodésique par rapport à . On a alors :

La figure ci-contre illustre la différence qui existe entre un élément structurant euclidien et un élément structurant géodésique. Sur cette figure, on a placé le disque sur différentes positions . Le disque euclidien reste le même indépendamment de la position x. Par contre, le disque géodésique change de forme ou peut disparaître en fonction de sa position. Du disque initial, il ne reste que ce qui vérifie la distance géodésique. Ainsi les points du disque qui ne sont pas commun avec sont ignorés (positions ). Si le centre du disque n’appartient pas à , alors le disque géodésique n’existe pas ().
Les transformations géodésiques de base pour les ensembles[modifier | modifier le code]
En plus de l’ensemble à transformer que l’on appellera (pour marqueur), il faut introduire l’ensemble de référence géodésique .
La dilatation géodésique[modifier | modifier le code]
On part de la définition euclidienne de la dilatation en remplaçant la boule euclidienne par la boule géodésique. On peut alors écrire : Ensuite, on répète cette opération élémentaire fois : Les figures suivantes illustrent l’effet d’une dilatation géodésique par un hexagone. Une composante connexe de l’ensemble ne peut être dilaté que si elle intersecte , sinon elle disparaît. La dilatation s’arrête lorsque les frontières de sont atteintes.
-
Ensemble de référence X (jaune et rouge) et marqueur M (rouge et bleu)
-
Dilatation géodésique (hexagone taille 15) de M dans X
-
Dilatation géodésique (hexagone taille 40) de M dans X
L’ensemble se comporte comme un masque dans lequel on peut modifier et se comporte comme un marqueur permettant d’envahir une composante connexe de .
L’érosion géodésique[modifier | modifier le code]
De la même manière, on introduit l’érosion géodésique en remplaçant la boule euclidienne par la boule géodésique dans l’expression définissant l’érosion. On peut donc écrire :Comme l’élément structurant utilisé est symétrique, on a dualité entre l’érosion et la dilatation géodésique. Cette dualité s’exprime de manière légèrement différente de celle du cas euclidien car c’est le complémentaire par rapport à qu’il faut prendre en compte. Cette relation de dualité s’écrit alors avec l’opérateur de différence symétrique :Les figures illustrent l’effet de l’érosion géodésique sur un ensemble par rapport à en utilisant un élément structurant hexagonal.
-
Ensemble de référence X (jaune et rouge) et marqueur M (rouge)
-
Érosion géodésique (hexagone taille 15) de M dans X
On remarque que les parties de , totalement incluses dans et n’ayant pas de frontières communes, s’érodent comme dans le cas euclidien. Lorsqu’il y a des frontières communes, celles-ci ne sont pas affectées par l’érosion.
La reconstruction pour les ensembles[modifier | modifier le code]
Définition de la reconstruction[modifier | modifier le code]
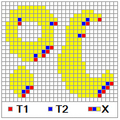
La reconstruction d’un ensemble à partir d’un autre est une des principales applications de la dilatation géodésique. On part donc de deux ensembles ; le premier est appelé l’ensemble des marqueurs noté , le second est l’ensemble de référence ou masque . Par définition, la reconstruction est une dilatation géodésique infinie, par rapport à , des marqueurs . Cela s’écrit :Lorsque toutes les composantes connexes contenant des marqueurs seront envahies, on ne pourra plus modifier l’image. Ceci constitue le test d’arrêt de la procédure. Les figures suivantes illustrent la reconstruction de à partir des marqueurs .
-
Ensemble de référence X (jaune et rouge) et marqueur M (rouge)
-
Reconstruction de X à partir des marqueurs M
Propriétés de la reconstruction[modifier | modifier le code]
Propriétés par rapport à l’ensemble de référence[modifier | modifier le code]
- La reconstruction est idempotente : la reconstruction s’arrêtant lorsque l’on ne modifie plus rien, elle vérifie cette propriété.
- La reconstruction est anti-extensive par rapport à : ne sont reconstruites que les composantes connexes contenant un marqueur.
- La reconstruction est croissante :La reconstruction correspond donc à une ouverture algébrique de l’ensemble de référence.
Propriétés par rapport aux marqueurs[modifier | modifier le code]
- La reconstruction est idempotente
- La reconstruction est extensive par rapport à :
- La reconstruction est croissante :
La reconstruction correspond donc à une fermeture algébrique des marqueurs.
Applications de la reconstruction pour les ensembles[modifier | modifier le code]
On ne citera ici que les plus importantes.
L’érosion reconstruction[modifier | modifier le code]
Dans l’érosion-reconstruction, les marqueurs seront les érodés euclidiens de et la dilatation euclidienne sera remplacée par la dilatation géodésique des marqueurs par rapport à l’ensemble . Cela s’écrit :Cette érosion-reconstruction est illustrée par les figures suivantes et comparée avec l’ouverture géodésique utilisant le même élément structurant.
-
Ensemble X1 (jaune et rouge) et érosion hexagonale de taille 11 (M1 = rouge)
-
Reconstruction de X1 à partir de M1
-
Ouverture géodésique de X1 (rouge : hexagone de taille 11)
Élimination des composantes connexes coupant le bord du champ d’image[modifier | modifier le code]
Pour certaines applications analytiques, il est nécessaire d’éliminer les composantes connexes de qui coupent le bord du champ d’observation . Pour cela, il faut les isoler en les reconstruisant à partir d’un marqueur constitué de tous les pixels du bord du champ , noté et les soustraire de . La procédure va donc être la suivante :L’ensemble ne contient que des composantes connexes totalement incluses dans . Ceci est illustré par les figures suivantes.
-
Ensemble X2 (jaune) et bord du champ dZ (rouge)
-
Composantes connexes de X2 reconstruites, coupant le bord du champ (rouge)
-
Composantes connexes de X2 totalement incluses dans le champ Z
Bouchage de trous[modifier | modifier le code]
La reconstruction est utilisée dans une opération qui sert souvent en traitement d’image : le bouchage de trous. Comme dans l’application précédente, le marqueur est . L’algorithme est le suivant :Les figures suivantes illustrent la séquence d’opérations.
-
Ensemble X3 (jaune) et bord du champ dZ (rouge)
-
Complémentaire de l'ensemble X3 (jaune) et bord du champ dZ (rouge)
-
Reconstruction du complémentaire de X3 à partir de dZ
-
Bouchage des trous de X3
Les érodés ultimes[modifier | modifier le code]
- Définition
Soit un ensemble présenté sur la figure suivante. Les érodés ultimes apparaissent au cours d’une succession d’érosions de par un élément structurant convexe. Ils sont constitués par l’union des composantes connexes qui disparaissent lors de l’érosion de taille immédiatement supérieure.

Soit une érosion digitale élémentaire, et son itérée d'ordre i. L'érosion ultime dérivée de et notée se définit alors comme le ‘’résidu’’ entre et les ouvertures par reconstruction de chaque érosion dans la précédente :Les érodés ultimes correspondent à l’union de toutes ces reconstructions en faisant varier de 1 à imax lorsqu’il n’y a plus rien par érosion.
- Propriétés des érodés ultimes
- L’érosion ultime est anti extensive.
- Les éléments constituants l’ensemble des érodés ultimes sont disjoints.
- Une érosion unitaire sur les érodés ultime donne un ensemble vide.
- L’érosion ultime est idempotente.
Ces érodés ultimes peuvent également être obtenus à partir des maxima de la fonction distance en utilisant une méthode géodésique pour les fonctions que l’on voit ci après. En restant dans le domaine ensembliste, les érodés ultimes servent à marquer les parties convexes des objets et peuvent être utilisés pour segmenter des agrégats de particules convexes.
Transformations géodésiques pour les fonctions[modifier | modifier le code]
Comme pour le cas ensembliste, on aura une fonction de référence et une fonction qui sera transformée . Les deux opérateurs de base sont toujours la dilatation géodésique et l’érosion géodésique.
Dilatation géodésique pour les fonctions[modifier | modifier le code]
La dilatation géodésique élémentaire de sous s’exprime de manière analogue à celle utilisée pour les ensembles.
Dans le cas des fonctions, ces éléments seront des éléments plats et convexes isotropes. On a, en effet :Pour une dilatation géodésique de taille quelconque, on aura également :
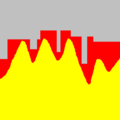
Interprétation sur une fonction f(x) définie dans R1-R[modifier | modifier le code]
Les images en niveaux de gris sont des fonctions définies dans . Pour faciliter la vision du comportement des opérateurs, on va utiliser une fonction définie dans . Soit également une fonction définie dans le même espace. Pour notre exemple, la seule possibilité est un ‘’élément structurant plat’’ constitué d’un ‘’segment droit’’ de longueur centré.
Les figures suivantes illustrent le cas d’une dilatation géodésique de taille .
-
Fonction f(x) (jaune et rouge) et marqueurs m1(x) (rouge)
-
Dilatation de taille 20 des marqueurs m1(x) (rouge) sous la fonction f(x) (jaune et rouge)
On remarque que les marqueurs dilatés restent toujours sous la fonction . Avec un élément structurant plat, il reste des parties de qui sont inaccessibles à la dilatation. Ce sont des parties convexes incluant les maxima.
On remarque que les marqueurs sont généralement choisis de telle sorte que l’on ait :
Érosion géodésique pour les fonctions[modifier | modifier le code]
Par définition, l’érosion géodésique élémentaire est donnée par :Comme pour la dilatation géodésique, on aura par itération :L’érosion géodésique pour les fonctions se déduit également de la dilatation géodésique pour les fonctions par dualité. Appelons ‘’le niveau de gris maximum supporté par l’image’’. On aura alors :
Cette expression est d’ailleurs celle utilisée pour construire n’importe quelle érosion géodésique.
Interprétation sur une fonction définie dans R1-R[modifier | modifier le code]
Les figures illustrent le comportement de l’érosion géodésique pour une fonction .
-
Fonction f(x) (jaune) et marqueurs m2(x) (jaune et rouge)
-
Érosion de taille 15 des marqueurs m2(x) (jaune et rouge) sur la fonction f(x) (jaune)
On remarque que la fonction érodée conserve des résidus dans les parties concaves de la fonction . Ce résultat est symétrique de celui obtenu par dilatation géodésique.
La reconstruction pour les fonctions[modifier | modifier le code]
Comme nous l’avons fait pour les ensembles, il est possible de reconstruire des fonctions géodésiquement par rapport à une autre fonction. Deux cas sont à envisager.
- La reconstruction de par dilatation géodésique infinie (ouverture)
- La reconstruction de par érosion géodésique infinie (fermeture)
La première figure illustre le résultat obtenu dans le cas de la reconstruction de sous la fonction et la seconde figure, la reconstruction de sur la fonction .
-
Reconstruction des marqueurs m1(x) (rouge) sous la fonction f(x) (jaune et rouge)
-
Reconstruction des marqueurs m2(x) (jaune et rouge) sur la fonction f(x) (jaune)
Application de la reconstruction pour les fonctions[modifier | modifier le code]
Maxima d’une fonction[modifier | modifier le code]
Les maxima régionaux d’une image sont les points de l’image à partir desquels il n’existe que des chemins descendants. Soit une image. À partir de cette image, on va construire une image des marqueurs en soustrayant un niveau de gris à . on aura donc :Ensuite, on effectue une reconstruction de sous et par différence avec , on obtient les maxima régionaux. On a donc :

Minima d’une fonction[modifier | modifier le code]
Pour la recherche des minima régionaux d’une fonction, on applique le même principe. Tout d’abord, on forme l’image des marqueurs :Ensuite, on effectue une reconstruction de sur et par différence avec , on obtient les minima régionaux. On a donc :

Maxima et minima étendus[modifier | modifier le code]
La recherche des maxima et minima d’une fonction donnent de très bons résultats si l’image n’est pas bruitée. En présence de bruit, la notion de maxima et de minima étendus, appelés aussi Hmax et Hmin, permet de n’extraire d’une image que les extrema significatifs. L’algorithme est semblable à celui des maxima et des minima. Seule, la construction des marqueurs est légèrement différente. En effet, au lieu de translater l’image d’un niveau de gris (en moins ou en plus), on effectue une translation de h niveaux de gris en plus ou en moins. Les Hmax et Hmin s’écrivent alors de la manière suivante.
Les figures suivantes illustrent la construction des Hmax dans le cas d’une fonction .
-
Fonction f(x) (jaune et rouge) et marqueurs m(-h) (rouge)
-
Fonction (fx) (jaune et rouge) et Hmax de f(x) (rouge)
A titre d’exemple, on montre le résultat dans le cas de l’image d’un pavage en niveaux de gris bruité. Les maxima régionaux de ce pavage sont inutilisables à cause du bruit. Par contre, les Hmax permettent de visualiser les plateaux de chaque pavé.
-
Image (en niveaux de gris) d'un pavage bruité
-
Maxima du pavage bruité
-
Hmax (h=30) du pavage bruité
-
Filtrage morphologique des Hmax par une ouverture de taille 1 suivie d'une fermeture de taille 10.
La recherche des maxima significatifs peut être améliorée par un filtrage de l’image binaire résultante, comme le montre la figure suivante. Les ‘’Hmin’’ sont obtenus et traités de manière analogue.
Segmentation[modifier | modifier le code]
Segmenter une image à niveaux de gris consiste à produire une partition du support de l'image, de façon que les régions de la partition correspondent aux objets présents dans l'image.
Les filtres morphologiques constituent une aide précieuse dans un processus de segmentation. En particulier, les nivellements permettent de filtrer les images tout en préservant les contours importants, ce qui simplifie l'opération de segmentation proprement dite. Dans certains cas, un filtrage important peut de lui-même produire une partition pertinente. Mais l'outil morphologique le plus connu en segmentation d'images est la ligne de partage des eaux.
Il existe plusieurs algorithmes de segmentation par ligne de partage des eaux. L'idée de base consiste à simuler une inondation de l'image, vue comme un relief topographique où le niveau de gris correspond à l'altitude. Les frontières entre régions de la partition ont alors tendance à se placer sur les lignes de crête. Typiquement, on applique cet opérateur au gradient de l'image (norme du gradient euclidien, ou gradient morphologique) que l'on cherche à segmenter, et par conséquent les frontières se placent de façon privilégiée sur les lignes de gradient élevé.
Plusieurs algorithmes de calcul de ligne de partage des eaux ont une complexité linéaire en fonction du nombre de pixels de l'image, ce qui les place parmi les méthodes de segmentation les plus rapides.
Quantification : Paramètres de base[modifier | modifier le code]
À l’origine la morphologie mathématique a été conçue pour traiter et analyser des images de matériaux ou images biologiques afin d’en extraire des informations quantifiées sous forme de paramètres ou de fonctions:. Ici, on se limitera aux images 2D définies dans l’espace et aux sous-espaces. Dans ce cas l’espace est représenté par une grille de points. Deux cas sont envisagés: la grille carrée (pavage carré) et la grille triangulaire (pavage hexagonal). En ce qui concerne les paramètres, on sait qu’ils peuvent être obtenus à partir de la caractéristique d’Euler-Poincaré ou nombre de connexité des différents espaces, notés pour l’espace .
Les nombres de connexité dans l’espace discret[modifier | modifier le code]
-
Pavage carré d'un ensemble X
-
Ensemble X et configuration de voisinage pour obtenir N1 (pavage carré)
-
Ensemble X et configurations de voisinage pour obtenir N2 (pavage carré)
Espace R0 : N0 (X)[modifier | modifier le code]
Cet espace correspond au réseau de points associés aux pixels.Sur l’image binaire, est égal au nombre de pixel à 1.
Espace R1 : N1 (X)[modifier | modifier le code]
Les droites utilisables dans correspondent à des pixels alignés. Les extrémités de segments de ces droites coupant correspondent (en sortie) à des transitions de pixel de type 1 0. L’image binaire associée est obtenue par une transformation en tout ou rien. D'un point de vue pratique cela revient à vérifier, pour chaque pixel , la configuration de voisinage . Les éléments 1 de la configuration sont relatifs à l’ensemble et ceux à 0 au complémentaire. On aura donc :Pour l'ensemble : Pour la mesure :
Les éléments structurants dans les différents pavages sont :
- En pavage hexagonal dans la direction 0 : .
(Les autres orientations à 60° et 120° sont obtenues par rotation de la configuration.)
- En pavage carré dans la direction 0 : .
(Les autres orientations à 45°, 90°, 135° sont obtenues par rotation de la configuration.)
Espace R2 : N2 (X)[modifier | modifier le code]
Rappelons que correspond au nombre de composantes connexes diminué du nombre de trous qu’elles contiennent.
- Pavage hexagonal
Pour déterminer ce nombre avec le pavage triangulaire, on utilise la relation d’Euler : En pavage hexagonal s représentant le nombre de sommets (pixels à 1), c le nombre de côtés de type 1-1 (à une rotation près) et f le nombre de triangles ayant les 3 sommets à 1. Un calcul élémentaire sur toutes les combinaisons donne le résultat suivant :Pour les ensembles : et Pour la mesure :
Les éléments structurants dans les différents pavages sont :
et .
- En pavage carré (8 connexité) on fait le même raisonnement ce qui donne les éléments structurants :
et .
Les paramètres métriques de base associés[modifier | modifier le code]
Comme pour les nombres de connexité, les paramètres métriques de base doivent vérifier les conditions de Hugo Hadwiger. L’ensemble doit être un ensemble aléatoire stationnaire et constitué d’une union finie de convexes. La mesure doit avoir les propriétés suivantes :
- Invariante par translation de :
- Compatible avec homothéties (agrandissement ) :
- C-additive :
- Continue ou semi continue
Dans R1[modifier | modifier le code]
Le paramètre métrique est la longueur totale de l’ensemble notée .Elle se calcule à partir de et la taille du pixel . On a en effet :
Dans R2[modifier | modifier le code]
Ces paramètres métriques sont:
- L’aire de l’ensemble notée
Elle se calcule à partir de et l’aire du pixel . On a en effet :
- Le périmètre de l’ensemble noté
Pour obtenir ce périmètre, on va utiliser la relation de Cauchy (géométrie intégrale) qui relie la variation diamétrale d'un ensemble à son périmètre : avec taille du pixel. On notera que l'estimation de ce périmètre à un aspect statistique. Le nombre de connexité doit être estimé dans plusieurs directions.
-
Illustration de la relation de Cauchy
-
Illustration de la relation de Crofton
-
Illustration de la relation de Meunier
Vers l'espace R3[modifier | modifier le code]
La géométrie intégrale permet également d’accéder à des paramètres de en utilisant les nombres de connexité des espaces inférieures.
- Ainsi, la surface de la frontière notée est obtenue à partir du nombre de connexité par la relation de Crofton : est la projection de sur le plan perpendiculaire à la direction et l'aire associée à la ligne .
- L'intégrale de courbure moyenne est estimée à partir de la variation diamétrale dans notée en utilisant la relation de Meusnier:Cette variation diamétrale est reliée au nombre de connexité dans par la relation :Ce qui donne finalement : représente la distance entre 2 plans.
De l’analyse globale à l’analyse locale (stéréologie [2])[modifier | modifier le code]
Les images destinées aux études scientifiques sont souvent obtenues à partir d’un microscope dont le champ est plus petit que l’ensemble à analyser. Dans ce cas, on dit que l’analyse est locale par opposition à l’analyse globale où l’ensemble est totalement visible.
Les paramètres globaux précédemment définis doivent être transformés en paramètres locaux ramenés à l’unité d’espace.
Paramètres locaux de l'espace R0[modifier | modifier le code]
- L’unique paramètre est la fraction de points :
Paramètres locaux de l'espace R1[modifier | modifier le code]
- Fraction linéique :Dans ce contexte statistique, on démontre aisément que l'estimation de la fraction linéique est égale à la fraction de points :
- Nombre de connexité par unité de longueur:
Paramètres locaux de l'espace R2[modifier | modifier le code]
- Fraction surfacique :On a également :
- Périmètre spécifique :En utilisant la relation de Cauchy, on obtient :
- Nombre de connexité par unité de surface :
Paramètres locaux de l'espace R3[modifier | modifier le code]
- Fraction volumique :Ici encore, on a :
- Surface spécifique :En utilisant la relation de Crofton, on a :
- Intégrale de courbure moyenne par unité de volume :L'intégrale de courbure moyenne peut être estimée à partir du nombre de connexité dans selon la relation de Meusnier :
- Nombre de connexité par unité de volume :Ce paramètre de nature topologique n'est pas accessible à partir des espaces de dimension inférieure.
Quantification 2 : Granulométrie et dispersion[modifier | modifier le code]
Les paramètres stéréologiques sont des paramètres moyens. De plus, ils ne sont pas nombreux. On conçoit aisément qu’ils soient insuffisants pour donner une description assez complète de la structure. Si l’on accepte de perdre l’aspect stéréologique, la morphologie mathématique permet d’obtenir de nombreuses informations quantitatives supplémentaires. Cette quantification dépend souvent d’un paramètre de taille associé aux transformations d’images. La quantification conduira à une opération de tri dont le dénombrement ou la mesure conduira à une fonction granulométrique. La dispersion d’un ensemble dans un autre est également quelque chose d’important à connaître. La stéréologie ne fournit qu’un paramètre dérivé qui est loin de répondre à la question.
L’analyse granulométrique[modifier | modifier le code]
Axiomes de l’analyse granulométrique (Georges Matheron)[modifier | modifier le code]
La méthode de tri doit vérifier les règles suivantes :
- La méthode de tri doit vérifier la propriété de croissance
- La méthode de tri est anti-extensive
- Dans le cas de deux tris successifs, c’est le paramètre le plus grand qui l’emporte. Le résultat est indépendant de l’ordre des opérateurs. Cela s’écrit : Cette dernière condition va réduire considérablement le nombre des opérateurs candidats.
Les fonctions granulométriques[modifier | modifier le code]
On distingue les granulométries en nombre et les granulométries en mesure.
- Si le tri granulométrique consiste à ne conserver que tout ce qui est plus petit que , alors la fonction de distribution granulométrique en nombre sera définie par :
- Au lieu de compter les objets, on peut reporter une mesure qui leur est associée (la masse dans un tamis).On obtient alors une fonction de distribution granulométrique en mesure définie par : En analyse d’image la mesure est le volume dans , l’aire pour et la longueur pour .
Analyse granulométrique individuelle[modifier | modifier le code]

Ce type d’analyse n’est possible que si l’ensemble à analyser est constitué d’une collection d’objets totalement disjoints. Chaque objet est isolé puis mesuré selon un critère de taille (aire, périmètre diamètre de Féret…). Le résultat de la mesure permet de mettre cet objet dans une classe de taille.
- Les problèmes du masque de mesure
Pour faire les mesures qu’on vient de citer, il est nécessaire que l’objet soit totalement inclus dans le champ de mesures. On doit donc éliminer ceux qui coupent le bord du champ. On a vu que cela est facilement réalisé par morphologie mathématique . Cependant, on a d’autant plus de chance d’éliminer un objet que sa taille est grande. Cela va introduire un biais dans l’analyse granulométrique. Pour résoudre ce problème, il faut pouvoir connaître la probabilité qu’un objet a d’être inclus dans le champ . Or, on a vu que donne l’ensemble des points de où est totalement inclus dans .

Ce raisonnement peut être transcrit pour résoudre notre problème en cherchant à éroder le masque rectangulaire par . Il est facile de voir qu’on obtiendra rigoureusement le même résultat si on remplace par le rectangle circonscrit minimum de même orientation que . La probabilité d’inclusion se calcule alors facilement : Dans cette expression, représente le côté horizontal et le côté vertical du champ (indice Z) ou du rectangle (indice R). Le biais sera alors corrigé en incrémentant la classe de taille non pas de 1 mais de . Cette méthode corrective a été proposée par Lantuéjoul.
Analyse granulométrique par ouverture avec un élément structurant à 2 dimensions[modifier | modifier le code]
Le milieu complémentaire des objets de la figure 1 ne peut pas être traité par cette méthode car la notion d’objet individuel n’a plus de sens. Cependant les axiomes de Matheron se vérifient lorsque l’ouverture est faite avec un élément structurant convexe. En effet, un élément structurant convexe permet de construire une famille de même nature dont tous les membres se déduisent de l’élément de taille 1 par un rapport d’homothétie de taille . Ce type de granulométrie est une granulométrie en mesure car l’ouverture ne possède pas de bonnes propriétés topologiques (un objet peut être scindé en deux par ouverture). Pour une image définie dans , la seule mesure utilisée est l’aire de l’ensemble ouvert.
-
Ensemble Booléen de disques circulaires (X= BD)
-
Ouverture hexagonale de taille 5 pixels sur BD et masque érodé (cyan)
-
Ouverture hexagonale de taille 20 pixels sur BD et masque érodé (cyan)
En analyse locale, il faut tenir compte du masque de mesure et donc travailler dans un masque érodé, on a donc : Il existe un cas particulier où la granulométrie peut être établie en nombre. C’est lorsque l’ensemble est constitué d’objets convexes disjoints. Dans ce cas, on aura :
Analyse granulométrique par ouverture avec un élément structurant linéaire[modifier | modifier le code]
L’élément structurant linéaire est traditionnellement noté . Les règles s’appliquent de la même manière que pour l’ouverture bidimensionnelle mais ici les granulométries en mesure et en nombre peuvent toujours se calculer puisque l’intersection d’un ensemble par une droite donne toujours des segments de droites convexes par définition. Les granulométries correspondantes sont données par les expressions suivantes pour les granulométries en mesure et les granulométries en nombre :
- Granulométries en mesure
- Granulométries en nombre
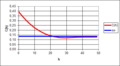
La fonction P(l)[modifier | modifier le code]
En fait, il n’est pas nécessaire de passer par l’ouverture pour obtenir ces granulométries, mais que l’on peut s’arrêter à l’érosion qui donne la fonction . Cette fonction est définie par :
Cette fonction possède un certain nombre de propriétés remarquables :
- La valeur à l’origine n’est autre que la teneur de la phase.
- La fonction décroît de manière monotone.
- La dérivée à l’origine, dans la direction , est égale, au signe près, au nombre de connexité spécifique pour cette même direction.
- La fonction possède des propriétés granulométriques.
-
Ensemble Booléen à grains Poissonniens (X = BP)
-
Érosion linéaire de taille 10 pixels sur BP et masque érodé (cyan)]
-
Érosion linéaire de taille 20 pixels sur BP et masque érodé (cyan)
D’après les relations précédentes, on a immédiatement : et
- La fonction a une propriété stéréologique avec la ‘’’notion d’étoile’’’.
Étoile bi et tridimensionnelle[modifier | modifier le code]
Supposons que l’ensemble soit transparent et que le complémentaire soit opaque. À partir d’un point appartenant à , on peut définir un domaine , constitué par tous les points y visibles de x. sera appelé ’’’ l’étoile de dimension 2’’’ associée au point x.

En recommençant la même opération pour tous les points de , on peut définir dans une étoile moyenne caractérisée par son aire. Cela s’écrit : Considérons l’élément de surface orienté selon . Cet élément appartient à l’étoile et aura pour probabilité conditionnelle le rapport : En utilisant la définition et en supposant le milieu isotrope, on a : Le même raisonnement peut être fait pour . L’étoile dans est définie par : Ce qui donne dans le cas isotrope : L’étoile dans définit un volume moyen en mesure et dans , une aire moyenne en mesure. Si est une union de convexes disjoints, l’étoile représente un ensemble convexe moyen. Puisqu’elle est mesurable à partir de , l’étoile a des propriétés stéréologiques.
Analyse de la dispersion[modifier | modifier le code]
L’étude de la dispersion suppose au moins un ensemble et son complémentaire, tous les deux non vide. Les paramètres stéréologiques qui ont été définis ne portent que sur un seul ensemble, l’analyse granulométrique également. En morphologie mathématique, il existe une fonction qui permet effectivement de tester l’état de dispersion d’un ensemble dans un autre. Cette fonction s’appelle la ‘’’fonction covariance’’’. Elle correspond à la mesure de l’érodé par un élément structurant constitué de deux points distants de h. Comme l’érosion est construite à partir de la soustraction de Minkowski, il est facile d’obtenir le résultat de l’érosion par h puisque cet élément structurant ne contient que 2 points distants de h. Pour cela, il suffit de translater l’image et de prendre l’intersection avec le translaté.

On aura donc :
La covariance simple[modifier | modifier le code]
La covariance est surtout utilisée dans le cas local. Dans ce cas, on définit la fonction covariance dans un masque de mesure Z par :
Propriétés de la covariance[modifier | modifier le code]
Comme la fonction , la fonction possède un certain nombre de propriétés. Ainsi, on a :
- La valeur à l’origine n’est autre que la teneur de la phase.
- La dérivée à l’origine.
- Entre l’origine et l’infini, la covariance est toujours inférieure à la valeur à l’origine. Les variations dans ce domaine dépendent de l’état de dispersion. En particulier, la présence de périodicité se traduit par des oscillations de la covariance et des paliers intermédiaires. Des paliers intermédiaires apparaissent pour des superpositions de structures à des échelles différentes. Des exemples sont donnés dans la section suivante.
- Dans le cas d’un ensemble aléatoire stationnaire, la valeur à l’infini correspond à la probabilité pour que 2 points indépendants tombent dans . C’est donc égal au carré de la teneur : Cette valeur est atteinte de manière asymptotique.
- Comme la covariance a un caractère directionnel, elle renseigne sur l’anisotropie de l’ensemble .
Exemples[modifier | modifier le code]
À titre d’exemple, nous prenons des cas limites :
- Un ensemble 2D isotrope (schéma booléen).
Dans l’exemple choisi la décroissance de la covariance se poursuit jusqu’à la valeur asymptotique. Comme l’analyse n’a été conduite que sur un champ, la concordance entre l’asymptote théorique et l’asymptote expérimentale n’est pas parfaite. Le léger passage par un minimum montre un petit effet de répulsion entre les disques.
- Un ensemble anisotrope composé de lamelles irrégulières (image d’un eutectique métallique).
L’aspect périodique de la structure se traduit par des oscillations de la courbe de covariance. Le premier minima correspond à une épaisseur moyenne d’une lamelle et le premier maximum à l’épaisseur moyenne du couple lamelle-complémentaire.
- Un ensemble constitué d’amas.
La covariance est plus complexe à interpréter mais on peut estimer ma distance moyenne entre amas.
-
Érosion par h(10 pixels) sur un ensemble Booléen de disques (X :jaune et rouge, érosion par h : rouge, érosion du masque : cyan)
-
Covariance sur l'ensemble Booléen de disques
-
Érosion par h(24 pixels) sur un ensemble lamellaire (X :jaune et rouge, érosion par h : rouge, érosion du masque : cyan)
-
Covariance sur l'ensemble lamellaire
-
Érosion par h(24 pixels) sur un ensemble d'amas (X :jaune et rouge, érosion par h : rouge, érosion du masque : cyan)
-
Covariance sur l'ensemble d'amas
Les modèles probabilistes (Ensembles aléatoires)[modifier | modifier le code]
Les paramètres stéréologiques sont peu nombreux et la caractérisation de la taille par des fonctions granulométriques a un caractère stéréologique uniquement pour les granulométries linéaires. Le même raisonnement peut être tenu pour la fonction covariance.
Si on accepte de rester dans l’espace, les autres granulométries, l’étude de la forme et de l’anisotropie permettent de compléter les informations morphologiques. Avec ces méthodes, on se trouve en possession d’un grand nombre de paramètres et de plusieurs distributions, mais en contrepartie, la lisibilité de la caractérisation n’est plus évidente.
Les modèles probabilistes constituent une autre approche beaucoup plus synthétique. Ils sont conçus pour caractériser des ensembles aléatoires. Bien entendu, tous les ensembles réels ne peuvent pas être décrits par de tels modèles. En premier lieu, ces ensembles doivent être, spatialement stationnaires [3], pour être facilement modélisables.
Généralités sur les modèles probabilistes[modifier | modifier le code]
Pour que l’on puisse observer une morphologie, il faut qu’un ensemble ne remplisse pas tout l’espace. On aura donc au minimum un milieu à deux composantes: l’ensemble et son complémentaire . Les objets constituant cet ensemble peuvent être aussi bien des points que des droites ou des sous-ensembles quelconques. L’ensemble , ainsi obtenu, sera donc un ensemble aléatoire topologiquement fermé dénommé RACS (RAndom Closed Set) et bien décrit dans les livres de Matheron, Serra, Stoyan et Jeulin. Cette restriction est importante pour conserver de bonnes propriétés, mais peu gênante dans la pratique. Ainsi, un RACS restera un RACS après une opération d’érosion de dilatation… Le choix d’un modèle dépend d’un certain nombre de connaissances a priori. Dans le cas des matériaux ou systèmes, le nombre de phases morphologiquement discernables est le premier élément. On aura donc deux grandes catégories :
- Les matériaux ou systèmes monophasés décrits à partir d’une partition de l’espace.
- Les matériaux ou systèmes polyphasés décrits à partir des RACS polyphasés.
La capacité de Choquet[modifier | modifier le code]
Un RACS peut être caractérisé par une probabilité d’événements correspondant à des mesures morphologiques comme la probabilité d’inclusion d’un compact dans un ensemble ou son complémentaire. C’est le rôle attribué à la capacité de Choquet définie par :
On peut aussi définir à partir de la probabilité que l’intersection entre et soit vide :

De la même façon qu’une fonction de distribution définit une variable aléatoire, la connaissance de la capacité de Choquet pour tout compact permet de définir complètement un modèle probabiliste. Il est évident que tous les compacts possibles ne peuvent pas être testés. On se contentera des plus simples.
Propriétés des RACS[modifier | modifier le code]
Les RACS peuvent vérifier ou non un certain nombre de propriétés.
L’infini divisibilité[modifier | modifier le code]
Un RACS est infiniment divisible si est équivalent à l’union de n RACS indépendants et de même nature. L’intersection d’un modèle infiniment divisible par un sous espace conserve la nature du modèle engendré. Ceci constitue une caractéristique de nature stéréologique. Pour un tel RACS et un compact donné, la capacité de Choquet est une expression de la forme :
avec :
La stabilité[modifier | modifier le code]
Un RACS infiniment divisible est stable par union si la fonction vérifie l’équation :
avec
La calculabilité[modifier | modifier le code]
Un RACS possède la propriété de calculabilité si pour certains compacts , les capacités de Choquet possèdent des formules explicites. Ceci permettra de vérifier si une structure réelle peut correspondre à la réalisation d’un RACS sans effectuer de simulation. Lorsque la capacité de Choquet n’est pas calculable, on peut utiliser des grandeurs caractéristiques liées aux paramètres du modèle.
Le processus ponctuel de Poisson[modifier | modifier le code]
Le point de départ de tous les modèles probabilistes est un processus ponctuel aléatoire. Il faut un processus où le nombre de points tombant dans un sous-ensemble soit indépendant de celui tombant dans . Le processus suivant la loi de Poisson vérifie cette condition. La probabilité pour que n points d’un processus de Poisson de densité appartiennent à un ensemble est donné par :
Les modèles ensemblistes de base[modifier | modifier le code]
Les partitions de l’espace[modifier | modifier le code]
Les modèles de partition aléatoire sont des ensembles qui découpent l’espace en plusieurs sous-ensembles fermés et bornés appelés classes. L’union de tous ses sous-ensembles remplit tout l’espace . Les principaux modèles de partition sont : la partition de Voronoï, la partition de Johnson Mehl, la mosaïque de Poisson et les feuilles mortes. Si tous ces modèles ont pour origine un processus ponctuel de Poisson, leur construction et leurs propriétés sont très différentes. Le dernier sera présenté après le modèle de Boole Matheron qui est un modèle polyphasé.
La partition de Voronoï[modifier | modifier le code]
Pour construire une partition ou diagramme de Voronoï, on implante des points selon un processus obéissant à la loi de Poisson de densité . À chaque point , correspond une zone d’influence qui est définie par :
avec la distance de à

Cette zone d’influence est un polygone convexe dans et un polyèdre convexe dans .
La simplicité du modèle a conduit de nombreux auteurs à l’utiliser pour décrire des structures cellulaires ou granulaires. Mais, la partition de Voronoï n’est pas infiniment divisible puisqu’une partition de Voronoï dans n’engendre pas une partition de Voronoï dans . De plus, on ne connaît pas d’expression analytique de la capacité de Choquet de cette partition pour les compacts usuels. Pour comparer une section plane de la structure réelle à un modèle de Voronoï dans , on dispose de quelques caractéristiques résumées par Miles, fonction de la densité de Poisson .
- Paramètres stéréologiques dans
- Périmètre spécifique :
- Nombre spécifique de cellules :
- Nombre spécifique de sommets :
- Paramètres moyens associés à une cellule
- Aire moyenne :
- Nombre moyen de sommets :
Dans le cas d’une partition de Voronoï dans , il existe des relations similaires utilisant la fonction et la densité de Poisson .
- Paramètres stéréologiques dans
- Surface spécifique :
- Longueur spécifique des joints triples :
- Nombre spécifique de cellules :
De plus, les densités de la partition et les fonctions "étoile" , , et sont reliées à la densité du processus de Poisson par les relations suivantes :
- Densité de la partition dans :
- Densité de la partition dans :
- Étoile dans :
- Étoile dans :
- Étoile dans :
Ces fonctions étoile sont calculées à partir des moments de la fonction , (probabilité d’inclusion d’un segment dans un grain).
On a :
- Densité de la partition dans : ,
- Densité de la partition dans : ,
- Étoile dans : ,
- Étoile dans : ,
- Étoile dans : .
Le modèle de Johnson Mehl[modifier | modifier le code]
Le modèle de Johnson-Mehl est également basé sur un processus ponctuel de Poisson. Cependant, le modèle est séquentiel (fonction du temps). Chaque séquence est composée de deux processus élémentaires :
- Création de germes ponctuels selon un processus de Poisson de densité
- Epaississement conservant l'homotopie des germes, d’épaisseur , selon une vitesse .
Cependant, tous les germes créés ne vont pas nécessairement donner naissance à un « grain ». Si le germe apparaît dans un grain déjà formé, il disparaît. La construction s’arrête lorsque le complémentaire des grains a complètement disparu. Les grains constituant la partition ont des frontières hyperboliques dans et hyperboloïdes dans . Elles ne sont donc pas toujours convexes, mais on connaît leurs caractéristiques, en particulier la fonction de distribution du nombre de voisins.
-
Construction du modèle de Johnson Mehl (quelques étapes)
-
Construction du modèle de Johnson Mehl (quelques étapes)
-
Construction du modèle de Johnson Mehl (quelques étapes)
-
Construction du modèle de Johnson Mehl (résultat final)
Comme dans le cas de la partition de Voronoï, le modèle de Johnson-Mehl ne possède pas de propriétés stéréologiques. Dans le cas ou est constant, il existe des relations liées à la fonction :
- Densité de la partition dans : ,
- Densité de la partition dans : ,
- Étoile dans : ,
- Étoile dans : ,
- Étoile dans : .
La partition de Poisson[modifier | modifier le code]
La partition de l’espace selon un processus de Poisson est faite par des droites de Poisson. Les droites de Poisson sont construites de la manière suivante. Soit une droite d’orientation comprise entre et et passant par l’origine du plan. Sur cette droite, on réalise un processus ponctuel de Poisson de densité . En chacun de ces points, on implante une droite de Poisson perpendiculaire à . Dans le cas d’une mosaïque isotrope, est constant et la valeur de est choisie selon une loi de probabilité uniforme.

L’espace est alors partagé en une infinité de polygones aléatoires appelés polygones de Poisson.

Une construction similaire dans l’espace conduira à un espace partagé en une infinité de polyèdres de Poisson. L’angle est alors compris entre 0 et stéradians. Les droites de Poisson sont remplacées par des plans de Poisson perpendiculaires à selon une densité .
À la différence du modèle de Voronoï, la mosaïque de Poisson possède des propriétés stéréologiques. D’une part, le paramètre du modèle permet de caractériser le polyèdre moyen par son volume moyen, , sa surface moyenne, et son intégrale de courbure moyenne, . On a en effet les relations :
D’autre part une mosaïque de Poisson dans , de paramètre , intersectée par un plan, génère une mosaïque de Poisson dans de paramètre avec :
La mosaïque de Poisson est rarement utilisée pour modéliser une partition de l’espace. Par contre, elle permet de générés des grains aléatoires pour des modèles polyphasés.
Un dernier mode de partition ne sera pas abordé dans cette section, il s’agit du modèle de feuilles mortes que nous verrons plus en détail dans la section suivante.
Les RACS multiphasés[modifier | modifier le code]
Les ensembles fermés aléatoires multiphasés constituent un groupe très important. On peut les classer en trois groupes.
- Le premier groupe est le ‘‘ modèle Boole Matheron ‘‘. C’est le plus connu de tous au même titre que la partition de Voronoï dans la catégorie précédente.
- Le deuxième groupe rassemble les ‘‘modèles de feuilles mortes‘‘ qui, comme le ‘‘modèle de Johnson Mehl’’ sont des modèles séquentiels.
- Le troisième groupe est une extrapolation, dans le cadre polyphasé, des partitions de l’espace. Ce sont les partitions multiphasées.
Le modèle de Boole Matheron[modifier | modifier le code]
Ce modèle, également appelé schéma Booléen, est construit de la manière suivante. En chaque point d’un processus de Poisson, de densité , on place un grain primaire. Le schéma Booléen est l’union de tous ces grains primaire (figure de gauche).
-
Ensemble de Boole Matheron (jaune), (30 germes, disques taille 20)
-
Ensemble de Boole Matheron (jaune), (disques de taille variable)
-
Ensemble de Boole Matheron à grains Poissoniens (jaune)
Pour cet ensemble, on a généré un processus ponctuel et remplacé chaque point par un dodécagone de taille unique (grain primaire). La seconde figure représente un modèle de Boole Matheron construit avec des disques de taille variable. Pour la dernière figure, les grains primaires du modèle sont des polygones de Poisson, obtenus par tirage au sort à partir d’une partition comme nous l’avons dans la section précédente.
Propriétés[modifier | modifier le code]
Le modèle de Boole Matheron possède de très bonnes propriétés. Il est infiniment divisible, stable et calculable. En effet, si est le grain primaire du schéma Booléen, on a la relation :
est l’espérance de la mesure de Lebesgue de l’ensemble dilaté par le compact .
La capacité de Choquet peut encore s’écrire :
est l’érosion du complémentaire de par le compact . Pour tester un modèle de Boole Matheron par la capacité de Choquet (ou la fonctionnelle complémentaire), il suffit d’estimer les teneurs des érodés par une ou plusieurs familles de compacts . Chaque famille étant définie par l’ensemble de compacts homothétiques. Un modèle de Boole Matheron sera défini par la densité de Poisson et le grain primaire caractérisé par une forme et une distribution de taille.
Si le grain primaire est convexe et de géométrie simple, le modèle de Boole Matheron sera calculable par les paramètres stéréologiques du grain moyen : . Dans le cas de grains sphériques, les paramètres stéréologiques sont calculables à partir des moments 3, 2 et 1 de la distribution granulométrique . On a, en effet, les relations :
Enfin, comme une union de modèles de Boole Matheron est toujours un modèle de Boole Matheron, on dispose de beaucoup de nombreuses solutions pour aborder la modélisation d'une structure réelle.
Certains compacts sont particulièrement intéressants pour tester un modèle de Boole Matheron. Ce sont les points , les segments , les hexagones de taille r , le bipoint et, pour certains modèles, le triplet de points défini par les sommets d’un triangle équilatéral . Pour les compacts convexes et en appelant la teneur de l’ensemble complémentaire, on a les relations suivantes :
Pour le bipoint , on utilise le covariogramme géométrique moyen à la place de la covariance . Le covariogramme est lié à la covariance par l’expression :
Dans le cas de grains de Poisson, on a :
Lorsqu’on a des grains sphériques, le covariogramme géométrique est fonction de la distribution. En appelant , la taille maximale du grain primaire, on a :
Le modèle de feuilles mortes[modifier | modifier le code]
Le modèle de feuilles mortes est un schéma booléen séquentiel. La version monophasée du modèle est due à Jeulin. La construction est la suivante. Des grains primaires sont générés par un processus de Poisson de densité . À la différence du schéma booléen, les grains peuvent se recouvrir. Les plus anciens peuvent disparaître sous les plus récents. Le processus peut être arrêté au bout d’un temps t. Si le support n’est pas entièrement recouvert, le processus ressemble un peu à un schéma booléen. On peut aussi poursuivre jusqu’à stationnarité. La partition recouvre alors intégralement le support.
Dans le cas d’un modèle de ‘‘feuilles mortes biphasé‘‘, les grains primaires de la phase 1 et de la phase 2 apparaissent successivement avec les densités respectives et . Le processus est répété jusqu’à stationnarité. Il reste une structure biphasée, où les deux phases sont imbriquées les unes dans les autres.
-
Construction d'un modèle de feuilles mortes biphasé avec des disques bleus et jaunes
-
Fin de la construction d'un modèle de feuilles mortes biphasé avec des disques bleus et jaunes
Ces modèles sont infiniment divisibles et donc ils génèrent des modèles équivalents dans des sous espaces. La calculabilité n’est pas aussi forte que dans le cas du schéma booléen. Les capacités de Choquet ne sont calculables que pour le bi point distant de h et pour le triplet de points distant de h . Lorsque le bi point est testé, on utilise la fonction définie par :
avec teneur de la phase 1 et celle de la phase 2 et
À titre d’illustration, on présente quelques réalisations avec des disques circulaires ou des polygones de Poisson comme grains primaires.
-
Modèle de feuilles mortes biphasé avec des disques bleus et jaunes
-
Modèle de feuilles mortes biphasé avec des grains Poissonniens bleus et jaunes
Les partitions de l’espace multiphasées : la partition de Poisson[modifier | modifier le code]
Pour construire une partition de Poisson polyphasée, il faut construire une partition monophasée et attribuer les classes à une phase donnée de manière aléatoire. Les paramètres du modèle (Miles) sont la teneur de chaque phase et qui caractérise la partition de Poisson. Dans le cas de la partition de Poisson biphasée, les propriétés du système monophasé sont conservées.

Les lois analytiques sont connues pour , et
Le modèle de Stienen[modifier | modifier le code]
Dans un modèle de Boole Matheron ou un modèle de feuilles mortes, les grains primaires peuvent se recouvrir. Pour construire le modèle de Stienen, on part toujours d’un processus ponctuel de Poisson de densité . Mais chaque point sera remplacé par la plus grande sphère contenue dans la cellule de Voronoï correspondante. Dans ces conditions, les sphères ne se recouvrent pas mais peuvent se toucher (figure de gauche). Il a été généralisé en réduisant la taille des sphères par un facteur (figure de droite).
-
Modèle de Stienen avec alpha = 1 (rouge) et partition de Voronoï associée (frontière bleue)
-
Modèle de Stienen avec alpha < 1 et partition de Voronoï associée (frontière bleue)
Dans le cas du modèle initial (), la teneur des sphères est constante puisque l’on a :
De plus, la distribution des sphères est connue puisqu’elle est directement liée à la distribution des distances des plus proches voisins d’un processus de Poisson. On a en effet :
Pour , les sphères ne sont plus en contact (figure 14). On peut calculer par intégration numérique la fonction de corrélation d’une paire de points en fonction de la distance r. Enfin, pour ce modèle, on ne dispose que d’une expression complexe de la covariance.
Notes[modifier | modifier le code]
- La dilatation est aussi souvent définie en utilisant le symétrique de l'élément structurant : On gagne alors la dualité entre érosion et dilatation, mais on perd l'adjonction. Il faut alors modifier les définitions de l'ouverture et de la fermeture morphologiques en conséquence. Lorsque l'élément structurant est symétrique, cette distinction n'a pas d'importance.
- La stéréologie traite de l'ensemble des méthodes permettant l'exploration de l'espace tridimensionnel à partir de mesures dans les espaces inférieurs.
- On dit qu'un ensemble est stationnaire lorsque les paramètres moyens décrivant l'ensemble sont indépendants de la position du champ de mesures.
Bibliographie[modifier | modifier le code]
En français[modifier | modifier le code]
- Georges Matheron, Éléments pour une théorie des milieux poreux, Masson, Paris, 1967.
- Michel Schmitt et Juliette Mattioli, Morphologie mathématique, Masson, Paris, 1993, (ISBN 2-225-84385-6) .
- Laurent Najman et Hugues Talbot (dir.), Morphologie mathématique, 1 : Approches déterministes, Hermès - Lavoisier, Paris, 2008, (ISBN 978-2746218413) .
- Laurent Najman et Hugues Talbot (dir.), Morphologie mathématique, 2 : Estimation, choix et mise en œuvre, Hermès - Lavoisier, 2010.
- Jean Marc Chassery, Annick Montanvert, Géométrie discrète en analyse d'images, Hermès, 1991, (ISBN 2-86601-271-2).
- H. Poincaré Calcul des probabilités. Carré, Paris, 1912.
- Michel Coster, Jean Louis Chermant, Précis d'analyse d'images, Presse du CNRS, 1989, (ISBN 2-87682-020-X) .
- Robert T. DeHoff, Frederick N. Rhines, Microscopie Quantitative, (traduit par Jean Montuelle), Masson 1972.
En anglais[modifier | modifier le code]
- Georges Matheron, Random Sets and Integral Geometry, Wiley, New York, 1975.
- Georges Matheron, Estimating and Choosing, Springer–Verlag Berlin, Heidelberg, 1989.
- Jean Serra, Image Analysis and Mathematical Morphology, vol. 1, Academic Press, Londres, 1982, (ISBN 0-12-637242-X) .
- Jean Serra (dir.), Image Analysis and Mathematical Morphology, vol. 2 : Theoretical Advances, Academic Press, Londres, 1988, (ISBN 0-12-637241-1) .
- Charles R. Giardina et Edward R. Dougherty, Morphological Methods in Image and Signal Procesing, Prentice-Hall, New Jersey, 1988.
- H.J.A.M Heijmans, Morphological image operators, Academic Press, coll. "Advances in Electronics and Electron Physics", Boston 1994.
- Pierre Soille, Morphological image analysis, Springer-Verlag Berlin, Heidelberg, 1999 (2e édition 2003).
- Gonzalez R.C., Woods R.E., Digital Image Processing, 3e éd., Prentice Hall, 2008.
- Goutsias J., Batman S., Morphological Methods for Biomedical Image Analysis, Handbook of Medical Imaging, volume 2 : Medical Image Processing and Analysis, M. Sonka & J.M. Fitzpatrick (eds.), SPIE Optical Engineering Press, 2000, p. 175-272.
- Laurent Najman and Hugues Talbot (Eds).Mathematical morphology: from theory to applications, ISTE-Wiley, (520 pp.) June 2010, (ISBN 978-1-84821-215-2) .
- Henri Poincaré, Papers on Topology: Analysis Situs and its Five Supplements, (traduit par John Stillwell), American Mathematical Society, Providence, R. I., 2010, (ISBN 978-0821852347) .
- E.E. Underwood, Quantitative Stereology, Addison Wesley, 1970.
- Luis A. Santaló, Integral Geometry and Geometric Probability 2nd édition, Cambridge Mathematical Library, 2004, (ISBN 978-0521523448) .
- Ewald R. Weibel, Stereological Methods. Vol. 1: Practical methods for biological morphometry , Academic Press, 1979, (ISBN 978-0127422015) .
- C. Lantuéjoul. On the estimation of mean values in individual analysis of particles, Microscopica Acta, 1980, 5, 266-273.
- Dominique Jeulin (editor), Advances in Theory and Application of Random Sets, World Scientific, 1997, (ISBN 978-9810230012).
- Sung Nok Chiu, Dietrich Stoyan, Wilfrid S. Kendall, Joseph Mecke, Stochastic Geometry and its Applications, Wiley Series in Probability and Statistics, 2013, (Online), (ISBN 978-1118658222).
- D. Jeulin, Multi-component random models for description of complex microstructures, Mikroscopie, 1980, 37, 130-137.
- G. Choquet, Theory of capacities, Ann. Inst. Fourier, 1953, 5, 131-295.
- R.E. Miles, The random division of space, Suppl. Adv. Prob., 1972, 243-266.
- R.E. Miles, Poisson flats in euclidean spaces. Part 2: homogeneous Poisson flats and the complementary theorem, Adv. Prob., 1971, 3, 1-43.
- H. Stienen, The sectionning of randomly dispersed particles, a computer simulation, Mikroskopie (Wien) 1980, S37, 74-78.
- M. Schlater, D. Stoyan, The covariance of the Stienen model. Advances in Theory and Application of Random Sets. World Scientific 1997, 157-174.
- D. Stoyan, K. Wiencek, Spatial correlation in metal structures and their analysis, Materials characterization, Elsevier Sc Pub. 1991, 26, 167-176.
En Allemand[modifier | modifier le code]
- Hugo Hadwiger, Vorlesungen über Inhalt, Oberfläche und Isoperimetrie, Springer-Verlag, Berlin u. a. 1957, (ISBN 3-540-02151-5) .
Articles connexes[modifier | modifier le code]
- Centre de morphologie mathématique
- Somme de Minkowski
- Ligne de partage des eaux (segmentation)
- Automate cellulaire


















































































































































































![{\displaystyle L_{2}(X)=\int _{0}^{\pi }D_{2}(X,\alpha )\times \mathrm {d} \alpha =\pi \times \mathbb {E} [{D(X)}]=\pi \times \mathbb {E} [{N_{1}(X)}]\times \mathrm {d} D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4fbec2c6d80ab7f3219598c9ca09e235550777e)








![{\displaystyle S(X)={\frac {1}{\pi }}\int _{0}^{4\pi }A(X',\omega )\times \mathrm {d} \omega =4\times \mathbb {E} [A(X')]=4\times \mathbb {E} [{N_{1}(X)}]\times \mathrm {d} A}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d99cbc8c2fe93efd62c272bd1875eaea26cb82b)





![{\displaystyle M(X)=2\pi \times {\mathbb {E} [D_{3}(X,\omega )]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10b59850bf9a130f5e1424cd481213a3839daaad)


![{\displaystyle M(X)=2\pi \times {\mathbb {E} [N_{2}(X,\omega )]\times \mathrm {d} D_{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff0fc81b0f2ce8aad10c067774d0eebeae6a7389)















































![Érosion linéaire de taille 10 pixels sur BP et masque érodé (cyan)]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1b/Morpho_Math_Granu_04b.png/120px-Morpho_Math_Granu_04b.png)











































































































![{\displaystyle Q(H(r))=q\times \exp(-\theta [-{\frac {3r}{4}}\times {\overline {S}}(X')+{\frac {3{\sqrt {3}}}{8}}\times r^{2}\times {\overline {M}}(X')])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cdeeba38bae2c832c38119c64b540b2fc44c9c5)




![{\displaystyle K(h)={\frac {\pi }{6}}\times \left[\int _{h}^{\infty }{a^{3}\times f(a)\times da}-{\frac {3h}{2}}{\int _{h}^{\infty }{a^{2}\times f(a)}\times da}+{\frac {h^{3}}{2}}{\int _{h}^{\infty }{f(a)}\times da}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4338a4b9b8e78c8a17b8208dc38c6eef960d442)














![{\displaystyle \alpha [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d324322b83fdf106059447cfcb24bfa7438c92ef)






