Modèle du ver élastique

Le modèle du ver élastique (ou modèle WCL) intervient en physique des polymères pour décrire le comportement des polymères semi-flexibles : c'est un modèle de molécule de raideur intermédiaire, dont les segments successifs pointent grossièrement dans une même direction, et dont la longueur de persistance approche est de quelques ordres de grandeur la longueur du polymère. C'est la version continue d'un modèle proposé par Otto Kratky et Günther Porod (1949).

Fondements du modèle

Schématisation du modèle du ver, avec le vecteur position et la tangente unitaire.

Plus élaboré que le modèle de chaîne idéale, où la macromolécule est assimilé à un assemblage de barres rigides articulées les unes aux autres, le modèle du ver considère la considère comme une verge élastique isotrope.

Ce modèle est particulièrement adapté à la description des polymères durs, dont les segments successifs manifestent une forme de comportement collectif, par lequel les segments voisins tendent à s'aligner. À température ambiante, le polymère affecte une courbure , qui devient nulle à $T=0$ K, pour former un bâtonnet rigide.

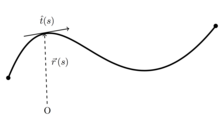
Pour un polymère de longueur maximum $L_{0}$, paramétrons la ligne moyenne de la macromolécule par $s\in (0,L_{0})$. Soit ${\hat {t}}(s)$ le vecteur tangent unitaire à la chaîne au point $s$, et ${\vec {r}}(s)$ le vecteur position le long de la chaîne, comme sur le schéma ci-contre. Comme ${\hat {t}}(s)\equiv {\frac {\partial {\vec {r}}(s)}{\partial s}}$, la distance entre les deux extrémités de la macromolécule est

${\vec {R}}=\int _{0}^{L_{0}}{\hat {t}}(s)ds$.

L'énergie de déformation du polymère s'écrit :

$E={\frac {1}{2}}k_{B}T\int _{0}^{L_{0}}P\cdot \left({\frac {\partial ^{2}{\vec {r}}(s)}{\partial s^{2}}}\right)^{2}ds$

où $P$ est la longueur de persistance caractéristique du polymère, $k_{B}$ la constante de Boltzmann, et $T$ la température absolue. Aux températures élevées, la distance entre les deux extrémités de la macromolécule sera nettement inférieure à la longueur maximum $L_{0}$. Les fluctuations thermiques, en effet, favorisent son enroulement en hélice.

Il est ainsi possible de calculer la fonction de répartition d’orientation du polymère ; on trouve qu'elle suit une décroissance exponentielle de constante 1/P :

$\langle {\hat {t}}(s)\cdot {\hat {t}}(0)\rangle =\langle \cos \;\theta (s)\rangle =e^{-s/P}\,$

Moyenne quadratique de la distance entre extrémités d'un brin de polymère en fonction de la longueur de persistance.

Voici une expression utile donnant la moyenne quadratique de la distance entre extrémités d'un brin de polymère :

$\langle R^{2}\rangle =\langle {\vec {R}}\cdot {\vec {R}}\rangle =\left\langle \int _{0}^{L_{0}}{\hat {t}}(s)ds\cdot \int _{0}^{L_{0}}{\hat {t}}(s')ds'\right\rangle =\int _{0}^{L_{0}}ds\int _{0}^{L_{0}}\langle {\hat {t}}(s)\cdot {\hat {t}}(s')\rangle ds'$

$\langle R^{2}\rangle =\int _{0}^{L_{0}}ds\int _{0}^{L_{0}}e^{-\left|s-s'\right|/P}ds'=2PL_{0}\left[1-{\frac {P}{L_{0}}}\left(1-e^{-L_{0}/P}\right)\right]$

Observez que lorsque $L_{0}\gg P$, $\langle R^{2}\rangle =2PL_{0}$. Cela permet de montrer que dans le modèle du ver des macromolécules, la longueur de Kuhn est égale au double de la longueur de persistance. Quand $L_{0}\ll P$, $\langle R^{2}\rangle =L_{0}^{2}$, et le polymère affecte le comportement d'un bâtonnet rigide. La figure ci-contre montre la rigidification lorsque la longueur de persistance augmente.

Comparaison entre le modèle du ver et les données expérimentales obtenues pour le déploiement de l' ADN-λ.

Portée pour la Biologie

Les données expérimentales tirées du dépliage de l'ADN des Phage lambda, où les forces ont été calculées à partir des fluctuations browniennes d'une bille attachée à l'ADN, sont données ci-contre. Le modèle, représenté par la ligne continue, est calé avec une longueur de persistance de 51,35 nm et un contour de 1 560,9 nm.

Parmi les macromolécules modélisables par ce procédé, et qui sont importantes en biologie, citons :

• ADN complet (longueur de persistance de 40-50 nm) and ARN (longueur de persistance de 64 nm)
• simple brin d'ADN (longueur de persistance de 4 nm)
• ARN non structuré (longueur de persistance de 2 nm)
• protéines non structurées (longueur de persistance de 0,6-0,7 nm)
• microtubules (longueur de persistance de 0,52 cm)
• Phage filamenteux

Déformation des molécules vermiformes

À mesure qu'on redresse le polymère, le spectre accessible des fluctuations thermiques s'amoindrit, et une force entropique s'oppose à tout effort externe tendant à redresser le polymère. On peut estimer cette force modératrice à partir de l'énergie mécanique totale du polymère :

$H=H_{\rm {elastic}}+H_{\rm {external}}={\frac {1}{2}}k_{B}T\int _{0}^{L_{0}}P\cdot \left({\frac {\partial ^{2}{\vec {r}}(s)}{\partial s^{2}}}\right)^{2}ds-xF$.

Ici, le périmètre est noté $L_{0}$, la longueur de persistance par$P$, l'allongement par $x$, et la force externe par $F$.

On voit que la molécule présente un comportement élastique non linéaire. On s'est servi d'équipements de laboratoires variés, de la microscopie à force atomique (AFM) aux pinces optiques, pour tenter de caractériser l'élasticité des tissus biologiques. La formule d'interpolation suivante l'approche à 15% près :

${\frac {FP}{k_{B}T}}={\frac {1}{4}}\left({\frac {1}{\sqrt {1-{\frac {x}{L_{0}}}}}}-1\right)+{\frac {x}{L_{0}}}$

Voici une approximation plus précise (erreur relative d'environ 0.01%) de la loi force-allongement :

${\frac {FP}{k_{B}T}}={\frac {1}{4}}\left({\frac {1}{\sqrt {1-{\frac {x}{L_{0}}}}}}-1\right)+{\frac {x}{L_{0}}}+\sum _{i=2}^{i=7}\alpha _{i}\left({\frac {x}{L_{0}}}\right)^{i}$,

avec $\alpha _{2}=-0.5164228$, $\alpha _{3}=-2.737418$, $\alpha _{4}=16.07497$, $\alpha _{5}=-38.87607$, $\alpha _{6}=39.49944$, $\alpha _{7}=-14.17718$.

Voici deux approximations de la loi force-allongement plus simples, précises à 1% :

${\frac {FP}{k_{B}T}}={\frac {1}{4}}\left({\frac {1}{\sqrt {1-{\frac {x}{L_{0}}}}}}-1\right)+{\frac {x}{L_{0}}}-0.8\left({\frac {x}{L_{0}}}\right)^{2.15}$

${\frac {x}{L_{0}}}={\frac {4}{3}}\left(1-{\frac {1}{\sqrt {{\frac {FP}{k_{B}T}}+1}}}\right)-{\frac {10e^{\sqrt[{4}]{900{\frac {k_{B}T}{FP}}}}}{{\sqrt {\frac {FP}{k_{B}T}}}\left(e^{\sqrt[{4}]{900{\frac {k_{B}T}{FP}}}}-1\right)^{2}}}+{\frac {\left({\frac {FP}{k_{B}T}}\right)^{1.62}}{3.55+3.8\left({\frac {FP}{k_{B}T}}\right)^{2.2}}}$

Élasticité et modèle du ver

On ne peut négliger la force de rappel en configuration déformée : les polymères ne se redressent que sous l'action de forces externes. On tient compte de cette compliance en faisant intervenir un paramètre matériel $K_{0}$ dans l'hamiltonien du système. Pour les macromolécules très déformées, l'hamiltonien est donné par :

$H=H_{\rm {elast}}+H_{\rm {enthalp}}+H_{\rm {externe}}={\frac {1}{2}}k_{B}T\int _{0}^{L_{0}}P\cdot \left({\frac {\partial ^{2}{\vec {r}}(s)}{\partial s^{2}}}\right)^{2}ds+{\frac {1}{2}}{\frac {K_{0}}{L_{0}}}x^{2}-xF$

On retrouve dans cette expression le terme entropique décrivant le changement de forme de la molécule, et un terme « enthalpique », qui décrit la déformation du polymère sous l'action d'une force externe. Plusieurs approximations ont été proposées pour la loi de comportement force-déformation décrivant le redressement de l'ADN en conditions physiologiques (pH quasi-neutre, force ionique d'environ 100 mM, température ambiante), avec des forces de l'ordre de 1 000 pN.

Aux faibles sollicitations (F < 10 pN), on a obtenu la formule interpolée suivante:

${\frac {FP}{k_{B}T}}={\frac {1}{4}}\left(1-{\frac {x}{L_{0}}}+{\frac {F}{K_{0}}}\right)^{-2}-{\frac {1}{4}}+{\frac {x}{L_{0}}}-{\frac {F}{K_{0}}}$.

Aux fortes déformations, l'approximation suivante est valide :

$x=L_{0}\left(1-{\frac {1}{2}}\left({\frac {k_{B}T}{FP}}\right)^{1/2}+{\frac {F}{K_{0}}}\right)$.

Au voisinage de l'état non déformé, une formule très précise :

${\frac {FP}{k_{B}T}}={\frac {1}{4}}\left(1-l\right)^{-2}-{\frac {1}{4}}+l+\sum _{i=2}^{i=7}\alpha _{i}\left(l\right)^{i}$,

avec $l={\frac {x}{L_{0}}}-{\frac {F}{K_{0}}}$. Les coefficients $\alpha _{i}$ sont les mêmes que ceux du paragraphe précédent.

Voici deux formules simplifiées donnant l'allongement en fonction de la force, et vice-versa :

${\frac {FP}{k_{B}T}}={\frac {1}{4}}\left({\frac {1}{\sqrt {1-{\frac {x}{L_{0}}}+{\frac {F}{K_{0}}}}}}-1\right)+{\frac {x}{L_{0}}}-{\frac {F}{K_{0}}}-0.8\left({\frac {x}{L_{0}}}-{\frac {F}{K_{0}}}\right)^{2.15}$

${\frac {x}{L_{0}}}={\frac {4}{3}}\left(1-{\frac {1}{\sqrt {{\frac {FP}{k_{B}T}}+1}}}\right)-{\frac {10e^{\sqrt[{4}]{900{\frac {k_{B}T}{FP}}}}}{{\sqrt {\frac {FP}{k_{B}T}}}\left(e^{\sqrt[{4}]{900{\frac {k_{B}T}{FP}}}}-1\right)^{2}}}+{\frac {\left({\frac {FP}{k_{B}T}}\right)^{1.62}}{3.55+3.8\left({\frac {FP}{k_{B}T}}\right)^{2.2}}}+{\frac {F}{K_{0}}}$

Bibliographie

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Worm-like chain » (voir la liste des auteurs).
• (de) O. Kratky et Günther Porod, « Röntgenuntersuchung gelöster Fadenmoleküle », Recueil des Travaux Chimiques des Pays-Bas, vol. 68, n^o 12,‎ 1949, p. 1106–1123 (DOI 10.1002/recl.19490681203)
• Marko et E. D. Siggia, « Stretching DNA », Macromolecules, vol. 28, n^o 26,‎ 1995, p. 8759–8770 (DOI 10.1021/ma00130a008, Bibcode 1995MaMol..28.8759M)
• C. Bustamante et J. F. Marko, « Entropic elasticity of lambda-phage DNA », Science, vol. 265, n^o 5178,‎ 1994, p. 1599–1600 (PMID 8079175, DOI 10.1126/science.8079175 , Bibcode 1994Sci...265.1599B)
• M. D. Wang, H. Yin, R. Landick, J. Gelles et S. M. Block, « Stretching DNA with optical tweezers », Biophysical Journal, vol. 72, n^o 3,‎ 1997, p. 1335–1346 (PMID 9138579, PMCID 1184516, DOI 10.1016/S0006-3495(97)78780-0, Bibcode 1997BpJ....72.1335W)
• C. Bouchiat et al., « Estimating the Persistence Length of a Worm-Like Chain Molecule from Force-Extension Measurements », Biophysical Journal, vol. 76, n^o 1,‎ janvier 1999, p. 409-413 (lire en ligne)