Système de racines
En mathématiques, un système de racines est une configuration de vecteurs dans un espace euclidien qui vérifie certaines conditions géométriques, et la base d'une notion très importante dans la théorie des groupes de Lie.
Les groupes de Lie et les groupes algébriques étant utilisés dans la plupart des parties des mathématiques, les systèmes de racines sont appliqués en de très diverses circonstances, et leur schéma de classification, sous la forme des diagrammes de Dynkin, intervient souvent sans relation évidente avec les groupes de Lie, par exemple dans la théorie des singularités.
Définitions
[modifier | modifier le code]Soit V un espace euclidien de dimension finie, muni du produit scalaire euclidien standard noté (·, ·). Un système de racines dans V est un ensemble fini de vecteurs non nuls (appelés racines) qui satisfont les propriétés suivantes :
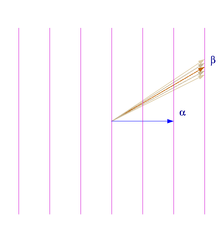
- Les racines engendrent V comme espace vectoriel.
- Les seuls multiples scalaires d'une racine qui sont dans sont elle-même et son opposé .
- Pour chaque racine l'ensemble est stable par la réflexion à travers l'hyperplan perpendiculaire à i.e. pour toutes racines et on a,
- (condition d'intégralité) Si et sont des racines dans , alors la projection orthogonale de sur la ligne engendrée par est un multiple demi-entier de :
En raison de la propriété 3, la condition d'intégralité est équivalente à l'énoncé suivant : et son image par la réflexion par rapport à diffèrent par un multiple entier de .
Le rang d'un système de racines est la dimension de V. On peut combiner deux systèmes de racines en faisant la somme directe des espaces euclidiens sous-jacents et en prenant l'union des racines. Un système de racines qui ne peut pas être obtenu de cette manière est dit irréductible.
Deux systèmes de racines et sont considérés comme identiques s'il existe une bijection de sur qui envoie sur et préserve les rapports de distances.
Le groupe des isométries de V engendré par les réflexions par rapport aux hyperplans associés aux racines de est nommé le groupe de Weyl de . Comme il agit fidèlement sur l'ensemble fini , le groupe de Weyl est toujours fini.
Classification
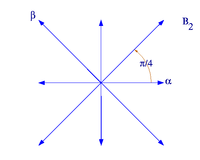
[modifier | modifier le code]Il existe seulement un système de racines de rang 1 constitué de deux vecteurs différents de zéro . Ce système de racines est appelé . Dans le rang 2, il existe quatre possibilités :

|

|
| Système de racines A1×A1 | Système de racines A2 |
|
|
| Système de racines B2 | Système de racines G2 |
Si est un système de racines dans V et W est un sous-espace de V traversé par , alors est un système de racines dans W. Ainsi, notre liste exhaustive de système de racines de rang 2 montre les possibilités géométriques pour deux racines quelconques dans le système de racines. En particulier, deux racines de cette sorte se rencontrent à un angle de 0, 30, 45, 60, 90, 120, 135, 150 ou 180 degrés.
En général, les systèmes de racines irréductibles sont précisés par une famille (indiquée par une lettre de A à G) et le rang (indiqué par un indice). Il existe quatre famille infinies (appelées les systèmes de racines classiques) et cinq cas exceptionnels (les systèmes de racines exceptionnels) :
Racines positives et racines simples
[modifier | modifier le code]Étant donné un système de racines , nous pouvons toujours choisir (de beaucoup de manières) un ensemble de racines positives. C'est un sous-ensemble de tel que
- pour chaque racine exactement une des racines est contenue dans ;
- Pour tous les tels que est une racine, .
Si un ensemble de racines positives est choisi, les éléments de () sont appelés racines négatives.
Le choix de est équivalent au choix des racines simples. L'ensemble des racines simples est un sous-ensemble de qui est une base de V avec la propriété spéciale que chaque vecteur dans lorsqu'il est écrit dans la base possède soit tous les coefficients ≥0 ou tous ≤0.
Il peut être montré que pour chaque choix de racines positives, il existe un unique ensemble de racines simples, c’est-à-dire que les racines positives sont exactement ces racines qui peuvent être exprimées comme une combinaison de racines simples avec des coefficients non-négatifs.
Matrice de Cartan
[modifier | modifier le code]Étant donné le système de racines simples (où est le rang du système de racines) on définit la matrice de Cartan par
L'intérêt de la matrice de Cartan est que sa seule donnée est suffisante pour reconstruire l'ensemble de tout le système de racines. C'est donc une façon théorique et pratique très utile de coder l'ensemble de l'information contenue dans un système de racines. Pour représenter graphiquement la matrice de Cartan on utilise le concept de diagramme de Dynkin qu'on va maintenant aborder.
Curieusement, la forme de Killing a été définie par Élie Cartan, tandis que la matrice de Cartan a été définie par Wilhelm Killing.
Diagrammes de Dynkin
[modifier | modifier le code]Pour démontrer ce théorème de classification, on peut utiliser les angles entre les paires de racines pour encoder le système de racines dans un objet combinatoire plus simple, le diagramme de Dynkin, nommé en l'honneur de Eugene Dynkin. Les diagrammes de Dynkin peuvent alors être classés selon l'arrangement donné ci-dessus.
À chaque système de racines est associé un graphe (probablement avec un bord particulièrement marqué) appelé le diagramme de Dynkin, unique à un isomorphisme près. Le diagramme de Dynkin peut être extrait du système de racines en choisissant un ensemble de racines simples.
Les sommets du diagramme de Dynkin correspondent aux vecteurs dans . Une arête est dessinée entre chaque paire de vecteurs non orthogonaux ; il y a une seule arête non orientée s'ils font un angle de 120 degrés, une double arête orientée s'ils font un angle de 135 degrés et une triple arête orientée s'ils font un angle de 150 degrés (on démontre en effet que deux éléments distincts de forment toujours un angle obtus). En plus, les doubles et triples arêtes sont marquées avec un signe d'angle pointant vers le vecteur le plus court.
Bien qu'un système de racines donné possède plus d'une base, le groupe de Weyl agit transitivement sur l'ensemble des bases. Par conséquent, le système de racines détermine le diagramme de Dynkin. Étant donnés deux systèmes de racines avec le même diagramme de Dynkin, nous pouvons faire coïncider les racines, démarrant avec les racines dans la base, et montrer que les systèmes sont en fait les mêmes.
Ainsi, le problème de classification des systèmes de racines se réduit au problème de classification des diagrammes de Dynkin possibles, et le problème de classification des systèmes de racines irréductibles se réduit au problème de classification des diagrammes de Dynkin connectés. Les diagrammes de Dynkin encodent le produit scalaire sur V en termes de base (par la notation des angles et des vecteurs courts), et la condition que ce produit interne doit être défini positif s'avère être tout ce qui est nécessaire pour obtenir la classification désirée. Les diagrammes connectés réels sont les suivants[1] :
| Diagramme | Nom du groupe |
|---|---|

|
|

|
|
|
|

|
|
Liste des systèmes de racines irréductibles
[modifier | modifier le code]La table suivante liste certaines propriétés des systèmes de racines irréductibles. Les constructions explicites de ces systèmes sont données dans les parties suivantes.
| I | ||||
|---|---|---|---|---|
| An | n(n+1) | n+1 | (n+1)! | |
| Bn | 2n2 | 2n | 2 | 2n n! |
| Cn | 2n2 | 2n(n−1) | 2 | 2n n! |
| Dn | 2n(n−1) | 4 | 2n−1 n! | |
| E6 | 72 | 3 | 51 840 | |
| E7 | 126 | 2 | 2 903 040 | |
| E8 | 240 | 1 | 696 729 600 | |
| F4 | 48 | 24 | 1 | 1 152 |
| G2 | 12 | 6 | 1 | 12 |
Ici désigne le nombre de racines courtes (si toutes les racines ont la même longueur, elles sont prises comme longues par définition), I désigne le déterminant de la matrice de Cartan, et désigne l'ordre du groupe de Weyl, i.e. le nombre de symétries du système de racines.
An
[modifier | modifier le code]Soit V, le sous-espace de ℝn+1 constitué des vecteurs dont la somme des coordonnées égale 0, et soit l'ensemble des vecteurs dans V de longueur √2 et qui sont des vecteurs entiers, i.e. qui ont des coordonnées entières dans ℝn+1. Un tel vecteur doit avoir toutes ses coordonnées sauf deux égales à 0, une coordonnée égale à 1 et une égale à - 1, donc, il existe racines en tout.
Bn
[modifier | modifier le code]Soit ℝn et soit constitué de tous les vecteurs entiers dans V de longueur 1 ou √2. Le nombre total de racines est .
Cn
[modifier | modifier le code]Soit ℝn et soit constitué de tous les vecteurs entiers dans V de longueur √2 en même temps que tous les vecteurs de la forme , où est un vecteur entier de longueur 1. Le nombre total de racines est .
Dn
[modifier | modifier le code]Soit ℝn et soit constitué de tous les vecteurs entiers dans V de longueur √2. Le nombre total de racines est .
E6, E7, E8
[modifier | modifier le code]Soit ℝ8. E8 désigne l'ensemble des vecteurs de longueur √2 tels que les coordonnées de soient toutes entières, toutes paires ou toutes impaires, et tels que la somme des 8 coordonnées soit paire.
En ce qui concerne E7, il peut être construit comme l'intersection de E8 avec l'hyperplan de vecteurs perpendiculaires à une racine fixée dans E8.
Finalement, E6 peut être construit comme l'intersection de E8 avec deux tels hyperplans, correspondant aux racines et qui ne sont ni orthogonales à une autre, ni des multiples scalaires à une autre.
Les systèmes de racines E6, E7 et E8 ont respectivement 72, 126 et 240 racines.
F4
[modifier | modifier le code]Pour F4, soit ℝ4, et soit désignant l'ensemble de vecteurs de longueur 1 ou √2 tel que les coordonnées de sont toutes entières et sont soit toutes paires ou toutes impaires. Il existe 48 racines dans ce système.
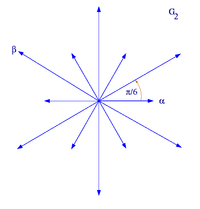
G2
[modifier | modifier le code]Il existe 12 racines dans G2, qui forment les sommets d'un hexagramme. Voir l'image ci-dessus.
Systèmes de racines et théorie de Lie
[modifier | modifier le code]Les systèmes de racines classent un nombre d'objets reliés dans la théorie de Lie, notamment :
- Les groupes de Lie simples et algèbres de Lie simples complexes
- Les groupes de Lie complexes simplement connexes qui sont simples modulo leur centre
- Les groupes de Lie compacts simples
Dans chaque cas, les racines sont les poids non nuls de la représentation adjointe.
Notes et références
[modifier | modifier le code]- La numérotation des racines indiquées n'est pas nécessaire car un diagramme de Dynkin n'est pas pondéré mais est indiquée seulement pour des raisons pratiques pour fixer une base lorsqu'on veut décrire explicitement le système de racines.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Root system » (voir la liste des auteurs).
















































