Lame à retard

Une lame à retard est un outil optique capable de modifier la polarisation de la lumière la traversant. Contrairement à un polariseur, l'état de polarisation de la lumière à la sortie de la lame dépend de l'état à l'entrée.
Généralités[modifier | modifier le code]
Cet effet vient de la biréfringence du cristal dans lequel est faite la lame (souvent du quartz ou du spath d'Islande) dont la forme est celle d'une lame à face parallèles[1]. En effet, un matériau biréfringent présente un axe privilégié appelé axe optique (c'est ainsi un matériau dit anisotrope). Or la polarisation de la lumière peut être décomposée en deux composantes : chaque composante ne se propage pas à la même vitesse selon qu'elle est parallèle ou perpendiculaire à l'axe optique (voir schéma ci-contre). Ceci permet de définir deux axes particuliers de la lame : l'axe lent et l'axe rapide.
Une lame à retard permet donc de retarder une de ces deux composantes par rapport à l'autre, c'est-à-dire de provoquer un déphasage. Ce retard dépend du matériau utilisé, de l'épaisseur de la lame, et de la longueur d'onde de l'onde lumineuse considérée.
Le phénomène de dispersion rend l'effet des lames à retard dépendant de la longueur d'onde de la lumière. Les lames sont donc prévues pour fonctionner dans une certaine gamme de longueur d'onde. Si l'on en sort, on obtient alors des aberrations chromatiques, c'est-à-dire une coloration de la lumière obtenue. Ce phénomène se retrouve aussi avec les lentilles.
La plupart des lames à retard sont taillées dans un cristal de façon que l'axe optique soit parallèle à la face de la lame. Ainsi les axes lent et rapide sont également parallèles à la face de la lame. Il existe plusieurs types de ces lames, caractérisées par le déphasage qu'elles produisent entre les deux composantes de la polarisation.
Formalisme de Jones[modifier | modifier le code]
Le formalisme de Jones est une représentation mathématique des ondes dites totalement polarisées c'est-à-dire telles qu'en tout point la direction de polarisation dépend du temps: la lumière totalement polarisée peut alors être représentée par un vecteur dit vecteur de Jones de la forme .
Une lumière totalement polarisée peut être dans trois différents états de polarisation[2]:
- la polarisation rectiligne: la lumière oscille dans une seule direction. Soient deux vecteurs orthonormés (ex,ey) telle que la direction de polarisation de la lumière soit dans le plan définis par ces vecteurs (ex,ey). Le vecteur de Jones représentant une lumière polarisée dans une telle direction est de la forme :
donc tel que φ=0 et avec θ l'angle tel que la direction de polarisation forme un angle θ avec le vecteur ex.
- la polarisation circulaire: les champs électriques et magnétiques de la lumière oscillent sur un cercle. Le vecteur de Jones correspondant est : avec . Le signe de l'angle φ dépendant du sens de parcours du cercle par le champ électromagnétique.
- la polarisation elliptique : les champs électriques et magnétiques de la lumière oscillent sur une ellipse. L'onde est alors représentée par un vecteur d'onde de la forme:
avec θ l'angle entre le demi grand axe de l'ellipse et ex. Le signe de φ détermine de même que la polarisation circulaire le sens de parcours de l'ellipse[3].
Dans le formalisme de Jones la matrice représentant un déphasage induit par une lame à retard est: [4].
Lames particulières[modifier | modifier le code]
Lame demi-onde[modifier | modifier le code]
Une lame demi-onde, également notée lame λ/2 est un instrument d'optique permettant de modifier l'état de polarisation de la lumière. Les lames demi-onde sont des lames à faces parallèles fabriquées dans un matériau biréfringent qui permettent d'introduire un retard de phase de la lumière de λ/2 entre les deux axes de biréfringence dits axe lent et axe rapide, c'est-à-dire un retard d'une moitié de longueur d'onde et un déphasage de 180°. Une telle lame comme toute lame à retard de phase est spécifiquement adaptée à une onde monochromatique donnée[5].
Les lames ½-onde sont les plus répandues des lames à retard[5]. Le retard induit, d'une demi-onde, permet pour une onde lumineuse polarisée selon un angle θ par rapport à l'axe lent d'obtenir une rotation du plan de polarisation de 2θ, puisque la composante sortante selon l'axe lent est en opposition de phase avec la composante entrante[5].
Une lame demi-onde est souvent utilisée à 45 degrés d'un polariseur rectiligne pour obtenir une polarisation croisée. L'ajout d'un analyseur dans la direction du polariseur entraîne alors une extinction.
Dans le formalisme de Jones, la matrice associée à la lame demi-onde est
pour un axe rapide horizontal.
Lame quart d'onde[modifier | modifier le code]
Une lame quart d'onde, également notée lame λ/4, est de même une lame à faces parallèles qui crée un déphasage de 90°, c'est-à-dire un retard d'un quart de longueur d'onde. Elle permet de passer d'une polarisation rectiligne à une polarisation elliptique voire circulaire, et vice versa. Elle est utilisée dans certaines lunettes 3D et les filtres polarisants circulaires pour la photographie (CPL en anglais : Circular Polarizing Lens filter).
Il existe aussi des lames taillées perpendiculairement à l'axe optique. Une onde ne subit alors aucun effet si elle arrive perpendiculairement à la face de la lame. Ce type de lames n'est donc intéressant que pour des rayons d'incidence oblique. Elles sont peu utilisées dans les instruments d'optique. Cependant, elles permettent d'étudier le pouvoir rotatoire du matériau dans lequel est faite la lame. En effet, la biréfringence n'étant pas visible, elle n'est pas prépondérante sur le pouvoir rotatoire.
Dans le formalisme de Jones, la matrice représentant l'action de la lame quart d'onde est
Applications[modifier | modifier le code]
Les lames à retard ont de nombreuses applications, les lames les plus fréquemment utilisées étant les lames quart d'onde et les lames demi-onde[5]. Elles serviront souvent à l'étude de la polarisation mais aussi seront utilisés dans certains secteurs industriels.
Applications à l'étude de la polarisation[modifier | modifier le code]
Une des applications basiques des lames à retard est de modifier la polarisation de la lumière. Dans le cas particulier des lames quart d'onde et des lames demi-onde, elles seront souvent utilisées pour transformer des lumières totalement polarisées, c'est-à-dire polarisées rectilignement, circulairement ou elliptiquement.
Changement de polarisation après traversée d'une lame demi-onde[modifier | modifier le code]
Une lumière polarisée est représentée par un vecteur . Après la traversée d'une lame demi-onde : l'onde sortant de la lame peut être représentée par le vecteur .
La lame demi-onde transforme donc une onde polarisée rectilignement ( ou ) en une onde polarisée rectilignement de direction de polarisation symétrique à la direction de polarisation de la lumière avant traversée de la lame par rapport à l'axe x et à l'axe y représentant les lignes neutres de la lame demi-onde et une lumière polarisée circulairement () en une onde polarisée circulairement parcourant le cercle dans le sens opposé à celui de l'onde entrant dans la lame. Une lumière polarisée elliptiquement est transformée en lumière polarisée elliptiquement de même ellipticité et l'ellipse est symétrique par rapport aux axes neutres de la lame avec l'ellipse parcouru par le champ électro-magnétique de l'onde entrant dans la lame[6].
| État de polarisation | |
| Avant la lame | Après la lame |

|

|

|

|

|

|
Changement de polarisation après traversée d'une lame quart d'onde[modifier | modifier le code]
Après traversée d'un lame quart d'onde le vecteur de Jones est .
Une lame quart d'onde transforme donc une lumière polarisée rectilignement () en une lumière polarisée elliptiquement (circulairement si ) sauf dans les cas où ou auquel cas la polarisation de la lumière ne change pas.
Une lame quart d'onde transforme une lumière polarisée elliptiquement en une lumière polarisée elliptiquement de même ellipticité à moins que auquel cas la lumière sortante de la lame quart d'onde a une polarisation rectiligne ou que (polarisation circulaire) la lumière résultante étant alors de polarisation rectiligne également[6].
| État de polarisation | |
| Avant la lame | Après la lame |
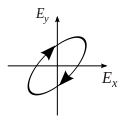
|

|

|

|

|

|
Mesure de la biréfringence avec une lame quart d'onde[modifier | modifier le code]
Une lame quart d'onde permet aussi de mesurer le déphasage d'une autre lame à retard et donc la biréfringence de cette lame avec un polariseur et un analyseur. Le système optique est constitué d'un polariseur suivi de la lame à étudier dont les axes neutres sont tournés à 45° par rapport à ceux du polariseur, et d'une lame quart d'onde dont les axes neutres sont parallèles avec ceux du polariseur et enfin d'un analyseur croisé avec le polariseur initialement. La manipulation en elle-même consiste en effet à tourner l'analyseur jusqu'à trouver l'annulation de la lumière sortant du système.
Pour mesurer la biréfringence, on éclaire le système avec une lumière d'une certaine longueur d'onde λ. Après traversée du polariseur la lumière arrive arrive sur la lame à étudier dont la polarisation deviendra alors elliptique, un des grands axes de l'ellipse étant alors confondu avec la direction de polarisation incidente par rapport à la lame à étudier, c'est-à-dire ici de par rapport aux axes de la lame. L'ellipticité de l'ellipse est alors donnée par la relation : , φ étant le déphasage introduit par la lame.
Or ce déphasage vaut avec δ différence de marche introduite par la lame et e épaisseur de la lame. On cherche donc à connaître l'ellipticité de l'ellipse représentant la polarisation de la lumière sortant de la lame à étudier. Les grands axes de cette ellipse sont parallèles aux axes neutres de la lame quart d'onde, la lumière sortant de la lame quart d'onde sera donc une lumière polarisée rectilignement dont la direction de polarisation forme un angle et avec les axes neutre de la lame quart d'onde.
En tournant l'analyseur d'un certain angle inférieur à , on constate une annulation de l'intensité lumineuse sortant de l'analyseur. En effet, en la direction de polarisation forme un angle ou avec l'axe optique de l'analyseur donc en tournant l'analyseur soit d'un angle soit d'un angle , l'intensité de la lumière sortant de l'analyseur s'annulera. Donc comme , on a avec k' entier d'où avec k entier et enfin .
Le facteur k et le signe devant α peuvent être déterminé en comparant avec une autre mesure, plus grossière de la biréfringence.
La lame quart d'onde en transformant une onde de polarisation elliptique en onde de polarisation rectiligne permet donc de mesurer assez précisément la biréfringence d'une lame à une certaine longueur d'onde λ.
Applications à l'industrie[modifier | modifier le code]
Laser[modifier | modifier le code]
Les lames à retard peuvent servir à différentes applications sur les lasers, nous détaillerons certaines de ces applications.
Une application consiste à tourner le plan de polarisation d'un laser polarisé dans certains cas où on ne peut pas le faire tourner à partir du laser seul avec une lame demi-onde[5].
On peut également modifier la fréquence d'un laser polarisé circulairement à l'aide d'une lame demi-onde. Si le faisceau laser traverse une lame demi-onde tournant à la vitesse angulaire , alors la fréquence du laser sera diminuée ou augmentée de f[8] selon le sens de la rotation de la lame par rapport à la polarisation du laser.
Lunettes 3D[modifier | modifier le code]

Il existe différents types de lunettes 3D, parmi eux des lunettes avec des verres constitués d'un polariseur et d'une lame quart d'onde ce qui constitue une application industrielle des lames quart d'onde. Ces verres permettent de reconstituer une image 3D qui utilise la polarisation[9].
Lors de la prise des images, deux caméras sont utilisées, chacune ayant un polariseur devant son objectif, ces deux polariseurs ayant des directions de polarisation orthogonales l'une par rapport à l'autre, selon un axe x et un axe y. Les caméras enregistrent alors une lumière polarisée circulairement, la composante selon l'axe x ne représentant que ce qui doit être vu par un des deux yeux lors de la projection et celle selon y devant être vue par l'autre œil[10].
Les lunettes 3D sont constituées de deux verres contenant chacun un polariseur suivi d'une lame quart d'onde. L'un des polariseurs polarise la lumière selon une direction x et l'autre selon la direction y. Il faut alors régler le retard des lumières envoyées à l'aide de lames quart d'onde permettant de n'avoir pas de retard entre une lumière et l'autre par rapport au moment de l'enregistrement de l'image, c'est-à-dire qu'on déphase une des ondes de et l'autre de [10].
Isolation optique[modifier | modifier le code]
Correction de la polarisation due aux réflexions[modifier | modifier le code]
Dans un système optique incluant des miroirs ou des surfaces réfléchissantes, l'état de polarisation d'une lumière polarisée arrivant sur les systèmes optiques se modifie le plus souvent. On utilise alors des lames à retard pour corriger la polarisation et ramener la lumière à l'état de polarisation souhaité.
Par exemple pour une lumière polarisée linéairement, à moins que la lumière arrivent normalement au plan du miroir ou que la direction de polarisation soit incluse dans le plan d'incidence, la réflexion change la polarisation de la lumière[5]. Il est alors possible de corriger l'état de polarisation en ajoutant une lame quart d'onde à la sortie du système : la polarisation devient ainsi de nouveau rectiligne.
Notes et références[modifier | modifier le code]
- [PDF]http://olivier.sigwarth.free.fr/CoursTS2/Ch8/Chap8.pdf
- [PDF]http://www.csvi.fr/Physique/Cours_files/TP%20O2%20Polarisation%20rectiligne%20de%20la%20lumie%CC%80re.pdf
- [PDF]http://www.impmc.jussieu.fr/~ayrinhac/documents/Polarisation_formalisme_de_Jones_%28S.Ayrinhac%29.pdf
- [PDF][1]
- « Lames d'onde », sur Newport (société)
- Physique tout en un sur Google Livres
- [PDF]« http://paristech.institutoptique.fr/site.php?id=937&fileid=11386 »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)
- Vélocimétrie laser pour la mécanique des fluides sur Google Livres
- [PDF]http://www.seigne.free.fr/TP/TPPolaris.pdf]
- [2]






























