Indice h
L'indice h (ou indice de Hirsch ou h-index en anglais) est un indice ayant pour but de quantifier la productivité scientifique et l'impact d'un scientifique en fonction du niveau de citation de ses publications. En résumé, un chercheur avec un indice de h a publié h articles qui ont été cités au moins h fois. Cet indice peut aussi s'appliquer à un groupe de scientifiques, tel qu'un département, une université ou un pays. Cet indice appartient à l'ensemble des métriques du niveau d'un auteur (en).
L'indice a été suggéré en 2005 par Jorge Hirsch comme un outil pour déterminer une qualité relative des physiciens théoriciens, cette mesure pouvant être étendue à tous les chercheurs publiant dans des revues à comité de lecture[1]. Hirsch suggère que, pour les physiciens, une valeur de 10-12 devrait permettre de considérer un poste de chercheur résidant dans une université renommée. Un poste de professeur pourrait être considéré à partir de 18, et 15-20 pour la qualité de membre de la Société américaine de physique. Une valeur supérieure à 45 pointerait vers la possibilité d'être admis à l'Académie nationale des sciences[2]. En janvier 2020 Jorge Hirsch revint cependant sur cette idée : « J'ai proposé l'index H en espérant qu'il serait une mesure objective d'accomplissement scientifique. Dans l'ensemble, je pense que cela est considéré comme étant le cas. Mais à présent, j'en suis venu à croire qu'il [l'index H] peut aussi échouer spectaculairement et avoir de sévères conséquences négatives involontaires. Je peux comprendre ce qu’a dû ressentir l'apprenti sorcier[3]. »
Définition et mesure[modifier | modifier le code]
L'indice est fondé sur la distribution des citations dont fait l'objet le travail d'un chercheur. D'après Hirsch : « Un scientifique a un indice h si h de [ses] Np articles ont chacun au moins h citations, et les autres (Np - h) articles ont au plus h citations chacun. »
Autrement dit, un chercheur avec un indice de h a publié h articles qui ont été cités au moins h fois[4]. Dès lors, l'indice h reflète à la fois le nombre de publications et le nombre de citations par publication. L'indice permet d'aller plus loin que la simple mesure du nombre d'articles ou de citations, tout en ne permettant qu'une comparaison des chercheurs à l'intérieur d'un même champ (les conventions de citation pouvant varier). En physique, un chercheur de niveau moyen devrait avoir un à peu près équivalent à la durée de sa carrière, tandis que pour les chercheurs en sciences biologiques et biomédicales cette valeur est généralement plus élevée.
Dans un modèle linéaire (où chaque article obtient chaque année le même nombre de citations), si on note le nombre de citations du y-ème article le plus cité alors[1] :
On obtient alors la formule : où est la somme totale d'articles, et est le nombre total de citations.
Exemple[modifier | modifier le code]
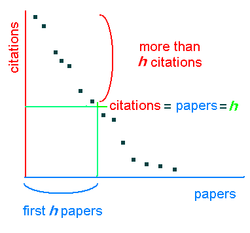
Formellement, si f est la fonction qui correspond au nombre de citations pour chaque publication, nous calculons l'indice h comme suit : nous ordonnons d'abord les valeurs de f de la plus grande à la plus petite valeur. Ensuite, nous cherchons la dernière position dans laquelle f est supérieur ou égal à la position (nous appelons h cette position). Par exemple, si nous avons un chercheur avec 5 publications A, B, C, D et E avec respectivement 10, 8, 5, 4 et 3 citations, l'indice h est égal à 4 car la 4e publication a 4 citations et la 5e n'en a que 3. En revanche, si les mêmes publications ont 25, 8, 5, 3 et 3 citations, alors l'indice est 3 (c'est-à-dire la 3e position) car le quatrième article n'a que 3 citations. De plus, l'indice n'est pas influencé par l'article très réussi.
f (A) = 10, f (B) = 8, f (C) = 5, f (D) = 4, f (E) = 3 → indice h = 4
f (A) = 25, f (B) = 8, f (C) = 5, f (D) = 3, f (E) = 3 → indice h = 3
Si nous avons la fonction f ordonnée par ordre décroissant de la plus grande valeur à la plus basse, nous pouvons calculer l'indice h comme suit :
indice h (f) =
Indice plus réaliste[modifier | modifier le code]
L'indice précédent ne fait pas apparaître la notion d'auteur unique ou coauteurs, ni la notion de premier auteur. Par ailleurs, dans le même article, Hirsch propose un indice qui se veut plus réaliste[1]. La généralisation est de ne plus donner une relation linéaire entre et h :
où et vérifient l'équation :
Indice h et auto-citations[modifier | modifier le code]
L'une des pratiques courantes des auteurs pour augmenter artificiellement leur indice h est de citer de manière disproportionnée leurs propres travaux, distorsion notée par Hirsch dans son article original[1]. Calculer un indice h corrigé pour tenir compte du ratio d'auto-citations est une tâche fastidieuse, car les moteurs de recherche tels que le Web of Science ou Google Scholar ne permettent pas de le calculer. Une étude heuristique a montré qu'en faisant l'hypothèse d'un ratio d'auto-citations constant (p), l'indice h peut être corrigé de la manière suivante pour obtenir un indice b[5] :
Critiques[modifier | modifier le code]
Il existe plusieurs situations où l'indice h peut induire en erreur à propos de la production scientifique[6]. La plupart de ces situations ne sont pas exclusives à l'indice h et peuvent s'appliquer à d'autres indicateurs bibliométriques.
- L'indice h ne tient pas compte du nombre de citations habituel dans différents domaines. Le comportement de citation varie beaucoup selon la discipline scientifique[7]. Cela invalide les comparaisons entre les disciplines, et même dans des spécialités d'une même discipline[8].
- Il ne tient pas compte de la position de l'auteur dans la liste des auteurs d'un article, ni du nombre de co-auteurs, alors que cela est important dans plusieurs disciplines[9],[10].
- Il prend en compte aussi bien les citations positives que négatives : c'est une mesure quantitative et non qualitative[11].
- Il ne prend pas en compte le biais de citation[11].
- Il ne serait qu'une simple fonction du nombre de citations, environ la racine carré divisée par deux du nombre total de citations[12].
- Une étude a trouvé que l'indice h avait une exactitude et une précision de prévision légèrement moindre qu'une simple mesure de la moyenne de citation par article[13]. Cependant, cette étude a été contredite par une autre étude de Hirsch[14].
- L'indice h est un entier naturel, ce qui réduit son pouvoir de discrimination. Ruane et Tol ont proposé un nombre rationnel qui effectue une interpolation entre h et h + 1[15].
- Il peut être manipulé par auto-citation[16],[17],[18].
- Il est fondé sur les données de Google Scholar, ce qui fait que même des documents générés par ordinateurs (ex: SCIgen) peuvent être utilisés pour manipuler l'indice h[19].
- Il ne fournit pas une mesure de l'impact scientifique plus précise que le nombre total de citations d'un chercheur. En particulier, Yong[20] a montré que la formule , où N est le nombre total de citations, est une approximation fiable de l'indice h dans la plupart des cas (avec des erreurs entre 10 et 20 pour cent).
- Il est la compilation de deux informations : le nombre de citations (impact) et le nombre de publications (productivité). Ce qui est un appauvrissement qualitatif puisque deux informations sont fusionnées en une seule.
- Enfin, plus généralement, cet indice ne reflète en rien l’impact de la recherche qui ne peut être réduit au taux de citation de publications par ses pairs, donc, qui ne concerne que les cercles, trop souvent fermés, des seuls initiés. Dans le monde réel, l’impact – sensu évaluation de projet de recherche-innovation-développement – d’une action de recherche est l’utilisation avérée de ses résultats à un niveau plus proche des bénéficiaires (décideurs, ingénieurs, agriculteurs, etc.), donc, dans le sens recherche vers innovation (un résultat de recherche utilisé) et développement (i.e., profite à la société qui finance cette recherche)[21].
Notes et références[modifier | modifier le code]
- (en) Jorge Hirsch, « An index to quantify an individual's scientific research output », Proceedings of the National Academy of Sciences, vol. 102, no 46, , p. 16569–16572 (DOI 10.1073/pnas.0507655102, lire en ligne)
- Ivars Peterson, « Rating Researchers », Science News Online, (consulté le )
- (en) Jorge E. Hirsch, « Superconductivity, What the H? The Emperor Has No Clothes », Physics and Society, , p. 5-9 (lire en ligne) :
« I proposed the H-index hoping it would be an objective measure of scientific achievement. By and large, I think this is believed to be the case. But I have now come to believe that it can also fail spectacularly and have severe unintended negative consequences. I can understand how the sorcerer’s apprentice must have felt. (p.5) »
- « Physicist Proposes New Way to Rank Scientific Output » (consulté le )
- « A simple method for excluding self‐citation from the h‐index: the b‐index », Online Information Review, vol. 33, , p. 1129-1136 (ISSN 1468-4527, DOI 10.1108/14684520911011043, lire en ligne, consulté le )
- (en) Michael C. Wendl, « H-index: however ranked, citations need context », Nature, vol. 449, no 7161, , p. 403–403 (DOI 10.1038/449403b, lire en ligne, consulté le )
- Lutz Bornmann et Hans‐Dieter Daniel, « What do citation counts measure? A review of studies on citing behavior », Journal of Documentation, vol. 64, no 1, , p. 45–80 (ISSN 0022-0418, DOI 10.1108/00220410810844150, lire en ligne, consulté le )
- Anauati, Maria Victoria and Galiani, Sebastian et Gálvez, Ramiro H., Quantifying the Life Cycle of Scholarly Articles Across Fields of Economic Research (November 11, 2014). Disponible à SSRN: http://ssrn.com/abstract=2523078
- (en) Cagan H. Sekercioglu, « Quantifying Coauthor Contributions », Science, vol. 322, no 5900, , p. 371–371 (ISSN 0036-8075 et 1095-9203, PMID 18927373, DOI 10.1126/science.322.5900.371a, lire en ligne, consulté le )
- (en) Chun-Ting Zhang, « A proposal for calculating weighted citations based on author rank », EMBO reports, vol. 10, no 5, , p. 416–417 (ISSN 1469-221X et 1469-3178, PMID 19415071, DOI 10.1038/embor.2009.74, lire en ligne, consulté le )
- (en) Nikolay K. Vitanov, Science Dynamics and Research Production: Indicators, Indexes, Statistical Laws and Mathematical Models, Springer, (lire en ligne), p. 65.
- (en) Ian Rownland, « Is it time to bury the h-index? », sur The Bibliomagician, (consulté le )
- (en) Sune Lehmann, Andrew D. Jackson et Benny E. Lautrup, « Measures for measures », Nature, vol. 444, no 7122, , p. 1003–1004 (DOI 10.1038/4441003a, lire en ligne, consulté le )
- (en) J. E. Hirsch, « Does the h index have predictive power? », Proceedings of the National Academy of Sciences, vol. 104, no 49, , p. 19193–19198 (ISSN 0027-8424 et 1091-6490, PMID 18040045, DOI 10.1073/pnas.0707962104, lire en ligne, consulté le )
- (en) Frances Ruane et Richard S. J. Tol, « Rational (successive) h-indices: An application to economics in the Republic of Ireland », Scientometrics, vol. 75, no 2, , p. 395–405 (ISSN 0138-9130 et 1588-2861, DOI 10.1007/s11192-007-1869-7, lire en ligne, consulté le )
- (en) Ramiro H. Gálvez, « Assessing author self-citation as a mechanism of relevant knowledge diffusion », Scientometrics, vol. 111, no 3, , p. 1801–1812 (ISSN 0138-9130 et 1588-2861, DOI 10.1007/s11192-017-2330-1, lire en ligne, consulté le )
- (en) Christoph Bartneck et Servaas Kokkelmans, « Detecting h-index manipulation through self-citation analysis », Scientometrics, vol. 87, no 1, , p. 85–98 (ISSN 0138-9130 et 1588-2861, DOI 10.1007/s11192-010-0306-5, lire en ligne, consulté le )
- (en) Emilio Ferrara et Alfonso E. Romero, « Scientific impact evaluation and the effect of self-citations: Mitigating the bias by discounting the h-index », Journal of the American Society for Information Science and Technology, vol. 64, no 11, , p. 2332–2339 (ISSN 1532-2890, DOI 10.1002/asi.22976, lire en ligne, consulté le )
- Labbé, Cyril (2010). Ike Antkare one of the great stars in the scientific firmament (PDF). Laboratoire d'Informatique de Grenoble RR-LIG-2008 (technical report). Université Joseph-Fourier.
- Alexander Yong, Critique of Hirsch’s Citation Index: A Combinatorial Fermi Problem, Notices of the American Mathematical Society, vol. 61 (2014), no 11, p. 1040–50.
- Vales M. 2017. Recurrent selection for populations-varieties obtaining - a new approach to merge modern methods and ancestral empirical know-how and genetic resources. Nov. 3rd, 2017, 云南农业大学农学与生物技术学院/College of Agriculture and Biotechnology, Yunnan Agricultural University, Kunming, Yunnan, China: 71 slides
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) H.L. Roediger, « The h Index in Science: A New Measure of Scholarly Contribution », Observer, vol. 19, (lire en ligne)
- Yves Gingras et Mahdi Khelfaoui, « Einstein vaut-il la moitié du Dr Raoult ? Pour en finir avec « l’indice h » », sur The Conversation, .
Articles connexes[modifier | modifier le code]
Lien externe[modifier | modifier le code]
- Index par journal et pays















