Filtre de Gabor
Un filtre de Gabor est un filtre linéaire dont la réponse impulsionnelle est une sinusoïde modulée par une fonction gaussienne (également appelée ondelette de Gabor). Il porte le nom du physicien anglais d'origine hongroise Dennis Gabor.
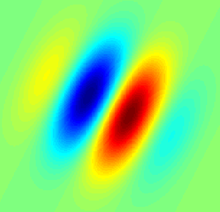
Expression temporelle (ou spatiale)[modifier | modifier le code]
Dans le domaine temporel (ou spatial s'il s'agit d'une image), un filtre de Gabor est le produit d'une sinusoïde complexe et d'une enveloppe gaussienne :
Ce qui donne en deux dimensions :
Il peut être pratique de la voir comme un couple de fonctions réelles, déphasées de . Il s'agit alors de la partie réelle et la partie imaginaire de la fonction complexe.
Dans le cas du traitement d'image (deux dimensions) cela donne par exemple :
où les variables a et b déterminent la fréquence et l'orientation du filtre. Le terme σ2 détermine son étendue en modifiant la variance de la gaussienne.
Expression fréquentielle[modifier | modifier le code]
Dans le domaine fréquentiel et dans le cadre d'une fonction non nulle, un filtre de Gabor est une gaussienne.
Principe et limitations[modifier | modifier le code]
Dans les transformées de Fourier, les compromis temps-fréquence optimaux pour minimiser les problèmes liés au principe d'incertitude sont obtenus pour les signaux gaussiens. Gabor a donc proposé une approche de l'analyse temps-fréquence non plus par des fenêtres rectangles, à durée finie, mais par des signaux gaussiens[1].
Il apparaît rapidement deux problèmes avec cette approche :
- contrairement aux signaux sinusoïdaux, la base de fonctions du filtre de Gabor n'est pas orthogonale ;
- alors que dans l'approche classique, le temps d'analyse T doit être choisi en fonction des fréquences basses, l'approche de Gabor va moyenner quelle que soit T, et c'est le paramètre σ qui fixe la résolution en fréquence.
Un moyen de pallier ce problème est de passer par une analyse en ondelettes, qui permet de construire une base de fonctions complètes orthogonales[1].
Relation avec la vision[modifier | modifier le code]
Dans le contexte de la vision, les filtres de Gabor correspondent aux informations parvenues au cortex visuel et fragmentées en petits paquets[2]. Certains auteurs[3] ont montré que les fonctions de Gabor présentent un niveau de plausibilité biologique de simulation des champs récepteurs de neurones biologiques visuels liés à différentes fréquences spatiales[4].
Références[modifier | modifier le code]
- Philippe Réfrégier, Théorie du signal : Signal-Information-Fluctuations, Masson, .
- « Ultimeyes : l'application qui booste votre vision à 11/10… », sur Huffingtonpost, .
- Daugman (1985), Jones & Palmer (1987) et Jones, Stepnoski & Palmer (1987).
- (en) Mermillod, M., Vuilleumier, P., Peyrin, C., Alleysson, D. et Marendaz, C., « The importance of low spatial frequency information for recognising fearful facial expressions », Connection Science, vol. 1, no 21, , p. 75-83 (DOI 10.1080/09540090802213974, lire en ligne).
Voir aussi[modifier | modifier le code]
- « Fischer, S., Sroubek, F., Perrinet, L., Redondo, R. and Cristóbal, G., “Self invertible Gabor wavelets”, International Journal of Computer Vision, 75, pp. 231-246, 2007 » (consulté le )





