Figure isotoxale
En géométrie, un polytope (un polygone, un polyèdre ou un pavage, par exemple) est isotoxal si son groupe de symétrie agit transitivement sur ses côtés. Informellement, cela veut dire qu'il y a un seul type de côté dans cet objet : pour deux côtés de l'objet, il y a une translation, une rotation et/ou une réflexion qui transforme un côté en l'autre, tout en laissant la région occupée par l'objet inchangée. Le terme isotoxal est dérivé du Grec τοξον qui veut dire arc.
Polygone isotoxal[modifier | modifier le code]
Un polygone isotoxal est un polygone équilatéral, mais les polygones équilatéraux ne sont pas tous isotoxaux. Par exemple, un pentagone équilatéral ayant un sommet "rentré" vers son intérieur n'est pas isotoxal (donc pas régulier).
En général, un 2n-gone isotoxal a une symétrie diédrale Dn (*nn) ; les mesures de ses angles alternent entre deux valeurs (au plus). Par exemple, un losange non carré : un 2×2-gone isotoxal, a une symétrie D2 (*22) ; il n'est pas régulier (car pas isogonal).
Tous les polygones réguliers (triangle équilatéral, carré, etc.) sont isotoxaux, en ayant le double de l'ordre de symétrie minimale : un n-gone régulier a une symétrie diédrale Dn (*nn). Par exemple, un carré : un 4-gone régulier, a une symétrie diédrale D4 (*44).
| Symétrie
diédrale |
D2 (*22) | D3 (*33) | D4 (*44) | D5 (*55) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Nom | Losange | Triangle équilatéral | Hexagone concave | Hexagramme | Carré | Octogone convexe | Pentagone régulier | Pentagramme | Décagramme |
| Image | 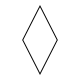
|

|

|

|

|

|

|

|

|
Les polygones isotoxaux sont les duaux des polygones isogonaux.
Polyèdres isotoxaux et pavages[modifier | modifier le code]

Un polyèdre ou un pavage isotoxal doit être ou isogonal (mêmes sommets), ou isoédral (mêmes faces), ou les deux.
Un polyèdre régulier est isoédral, isogonal et isotoxal. Les polyèdres quasi réguliers sont isogonaux et isotoxaux, mais pas isoédraux ; leur duaux sont isoédraux et isotoxaux, mais pas isogonaux.
Les polyèdres ou les pavages bidimensionnels construits à partir de polygones réguliers ne sont pas forcément isotoxaux. Par exemple, l'icosaèdre tronqué ("ballon de football") a deux types de côtés : hexagone-hexagone et hexagone-pentagone, donc n'est pas isotoxal (donc pas régulier) ; en effet, une symétrie de solide ne peut pas transformer un côté hexagone-hexagone en un côté hexagone-pentagone.
Un polyèdre isotoxal possède le même angle dièdre pour tous ses côtés.
Il y a neuf polyèdres isotoxaux convexes : dérivés des solides de Platon, huit concaves : dérivés des solides de Kepler-Poinsot, trois comme polyèdres étoilés quasi-réguliers ditrigonaux (3 | p q), et trois comme leurs duaux.
Notes et références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « isotoxal figure » (voir la liste des auteurs).
Voir aussi[modifier | modifier le code]
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, (ISBN 0-521-55432-2), p. 371 Transitivity
- (en) Grünbaum, Branko; and Shephard, G. C., Tilings and Patterns, New York, W. H. Freeman, (ISBN 0-7167-1193-1) (6.4 Isotoxal tilings, 309-321)
