Algorithme de Christofides
L'algorithme de Christofides est un algorithme d'approximation pour le problème du voyageur de commerce, dans le cas métrique, et que l'inégalité triangulaire est respectée. L'analyse de cet algorithme est due à Nicos Christofides and Anatoliy I. Serdyukov, qui l'ont découvert indépendamment en 1976[1],[2],[3].
Problème du voyageur de commerce métrique[modifier | modifier le code]

Le problème du voyageur de commerce (dans sa version optimisation[4]) est le problème suivant : étant donné un ensemble de villes reliées entre elles par des routes, trouver l'itinéraire le plus court passant par chaque ville une et une seule fois. En termes de graphe, on cherche le cycle hamiltonien le plus court. C'est un problème d'optimisation NP-difficile classique[5].
Plusieurs cas particuliers ont été étudiés, notamment le cas dit « métrique » où les arêtes respectent l'inégalité triangulaire c'est-à-dire que pour tout triplet de sommet , on a .
Algorithme[modifier | modifier le code]
Dans le cas général, cet algorithme est en fait une heuristique, cependant dans le cas métrique, on peut montrer que la solution est au plus 3/2 fois plus longue que l'optimal. On dit que le facteur d'approximation est de 3/2.
L'algorithme résout deux sous-problèmes considérés «faciles», car appartenant à la classe P : le problème de l'arbre couvrant de poids minimal[6] et celui du couplage de poids minimum[7].
Pseudo-code[modifier | modifier le code]
En pseudo-code[8] :
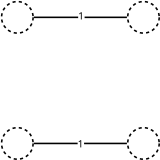
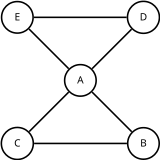
- Calculer un arbre couvrant de poids minimal de ;
- Soit l'ensemble des sommets de degré impair dans , calculer un couplage parfait de poids minimum dans le sous-graphe induit par les sommets de ;
- On définit un multigraphe à partir des arêtes issues de et ;
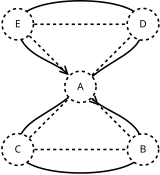
- Trouver un cycle eulérien dans (H est eulérien car il est connexe et tous les sommets sont de degré pair) ;
- Transformer le cycle eulérien en un cycle hamiltonien en supprimant les éventuels passages en double sur certains sommets.
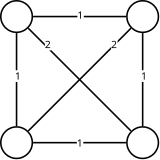
Exemple[modifier | modifier le code]
Facteur d'approximation dans le cas métrique[modifier | modifier le code]
Soit le cycle hamiltonien de poids minimum, et son poids.
L'arbre couvrant de poids minimum est de poids inférieur ou égal au poids de U (c'est-à-dire ), car en enlevant une arête au cycle on obtient un arbre couvrant.
Le couplage trouvé par l’algorithme est de poids inférieur ou égal à . En effet, si on considère le cycle hamiltonien de poids minimum sur le sous graphe induit par les sommets de degré impair, on a un poids inférieur ou égal à du fait de l'inégalité triangulaire, et en prenant une arête sur deux de ce cycle (qui est de longueur paire puisque constitué d'un nombre pair de sommets) on obtient un couplage qui est de poids inférieur à la moitié du poids du cycle (si ce n'est pas le cas on peut prendre le complémentaire).
D'où un poids final majoré par : noter que la transformation du cycle eulérien en cycle hamiltonien ne peut pas faire croître le poids grâce à l'inégalité triangulaire.
Complexité de l'algorithme[modifier | modifier le code]
L'algorithme a une complexité cubique[9].
Variantes[modifier | modifier le code]
Pour le problème du chemin hamiltonien (Path TSP), qui est la variante du problème du voyageur de commerce où un départ et une arrivée sont imposées, des variantes de l'algorithme de Christofides sont utilisées pour obtenir de bonnes approximations[10],[11].
Contexte et historique[modifier | modifier le code]
Le problème dans le cas métrique est APX-difficile, même avec des poids 1 ou 2[12], ce qui empêche l'existence d'un schéma d'approximation en temps polynomial. Le facteur de 3/2 est en fait le meilleur facteur connu[13].
Dans son article, Christofides a amélioré le facteur d'approximation du problème de 2 à 3/2[9]. Il a en fait affiné l'algorithme précédent qui consistait à construire un arbre couvrant minimal et à le parcourir[14].
Depuis les années de 2010, une nouvelle approche basée sur l'algorithme, appelée best-of-many, a permis de faire avancer certains cas particuliers et se révèle plus efficace dans la pratique[15]. Elle consiste schématiquement à utiliser l'algorithme de Christofides, sur plusieurs instances définies à partir d'une solution à la relaxation de Held et Karp[16].
Notes et références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Christofides algorithm » (voir la liste des auteurs).
- (en) Nicos Christofides, Worst-case analysis of a new heuristic for the travelling salesman problem, Graduate School of Industrial Administration, CMU, (lire en ligne), Report 388.
- René van Bevern et Viktoriaa A. Slugina, « A historical note on the 3/2-approximation algorithm for the metric traveling salesman problem », Historia Mathematica, (DOI 10.1016/j.hm.2020.04.003, arXiv 2004.02437, S2CID 214803097).
- (ru) Anatoliy I. Serdyukov, « О некоторых экстремальных обходах в графах », Upravlyaemye Sistemy, vol. 17, , p. 76–79 (lire en ligne).
- Au sens de problème d'optimisation par contraste avec le problème de décision associé.
- Présent notamment dans la liste des 21 problèmes NP-complets de Karp : (en) Richard M. Karp, « Reducibility Among Combinatorial Problems », dans Raymond E. Miller et James W. Thatcher, Complexity of Computer Computations, Plenum, (ISBN 978-1-4684-2003-6, DOI 10.1007/978-1-4684-2001-2_9, lire en ligne), p. 85-103.
- Pour lequel on peut utiliser par exemple les algorithmes polynomiaux de Prim, Kruskal ou Borůvka.
- Par exemple avec l'algorithme d'Edmonds pour les couplages.
- Adapté de « Présentation et preuve de l'algorithme (par Alain Hertz) » (consulté le ).
- Christofides 1976
- JA Hoogeveen,, « Analysis of Christofides' heuristic: Some paths are more difficult than cycles », Operations Research Letters, Elsevier, vol. 10, no 5, , p. 291-295
- Hyung-Chan An, Robert Kleinberg et David B. Shmoys, « Improving christofides' algorithm for the s-t path {TSP} », dans Proceedings of the 44th Symposium on Theory of Computing Conference (STOC) 2012, New York, NY, USA, May 19 - 22, 2012, , p. 875-886
- Voir Christos H. Papadimitriou et Mihalis Yannakakis, « The traveling salesman problem with distances one and two », Mathematics of Operations Research, INFORMS, vol. 18, no 1, , p. 1--11. Dans le cas des poids 1-2, l'article montre aussi que l'on peut obtenir une meilleure approximation : 7/8.
- Le problème du voyageur de commerce métrique (Minimum metric traveling salesperson) sur le Compendium of NP optimization problems.
- Une description précise et un survey sur le TSP peuvent être trouvés dans Laporte 1992.
- Kyle Genova et David P. Williamson, « An Experimental Evaluation of the Best-of-Many Christofides' Algorithm for the Traveling Salesman Problem », dans Algorithms - {ESA} 2015 - 23rd Annual European Symposium, Patras, Greece, September 14-16, 2015, Proceedings, (DOI 10.1007/978-3-662-48350-3_48), p. 570--581
- Voir l'article Problème du voyageur de commerce.
Bibliographie[modifier | modifier le code]
- Nicos Christofides, « Worst-case analysis of a new heuristic for the travelling salesman problem », Technical Report 388, Graduate School of Industrial Administration, Carnegie-Mellon University, Pittsburgh,
- (en) Gerhard Reinelt, The Traveling Salesman, Computational Solutions for TSP Applications, vol. 840, Springer, coll. « Lecture Notes in Computer Science », , 223 p. (ISBN 978-3-540-58334-9, BNF 37482407, lire en ligne)
- Gilbert Laporte, « The traveling salesman problem: An overview of exact and approximate algorithms », European Journal of Operational Research, vol. 59, no 2, , p. 231-247
Liens externes[modifier | modifier le code]
- « Présentation et preuve de l'algorithme (par Alain Hertz) » (consulté le )
- Le problème du voyageur de commerce métrique (Minimum metric traveling salesperson) sur le Compendium of NP optimization problems.