Variogramme
Le variogramme est une fonction mathématique utilisée en géostatistique, en particulier pour le krigeage. On parle également de semivariogramme, de par le facteur ½ de sa définition.
L'analyse variographique, variographie, ou analyse structurale est l'estimation et l'étude d'un variogramme sur une variable aléatoire.
Variogramme d'une fonction aléatoire[modifier | modifier le code]
Considérons une variable aléatoire, Z de la variable d'espace x, et supposons-la stationnaire, c'est-à-dire que la moyenne et la variance de Z(x) sont indépendantes de x. On pose la grandeur: Comme Z est stationnaire, le membre de droite dépend uniquement de la distance entre les points x et y. Le variogramme à une distance h est alors la demi moyenne des carrés des différences des réalisations de Z sur les points espacés de h.
Variogramme borné[modifier | modifier le code]
Théorème — Si Z est une fonction aléatoire stationnaire de covariance C, alors son variogramme est borné et s'écrit :
La réciproque est fausse : si Z est intrinsèque et de variogramme borné, alors Z est la somme d'une fonction aléatoire stationnaire de L2 et d'une variable aléatoire réelle.
Intérêt du variogramme[modifier | modifier le code]
Le variogramme est défini pour toute fonction aléatoire intrinsèque et dépendant uniquement de l'interdistance h, alors que la fonction de covariance ne l'est que pour le cas d'une fonction aléatoire stationnaire d'ordre 2. De plus, l'estimation du variogramme n'est pas biaisée par la moyenne, au contraire de la covariance.
Paliers et portée[modifier | modifier le code]
Si la covariance de Z tend vers 0 à l'infini, le variogramme présente un palier γ(∞) = Var[Z]. On nomme portée la distance à partir de laquelle le variogramme atteint, respectivement, son palier ; la portée pratique (parfois facteur d'échelle) est la distance à partir de laquelle le variogramme reste dans un intervalle de 5 % autour de son palier. La norme est le rapport de la portée sur la portée pratique.
Variogramme expérimental[modifier | modifier le code]
Le variogramme expérimental ou variogramme empirique est un estimateur du variogramme théorique à partir des données.
Soit un ensemble de points où sont connus les valeurs d'une variable régionalisée z. Pour être exploitable, la somme doit se faire avec une certaine tolérance, c'est-à-dire que l'on réalisera la somme sur les couples interdistants de h±δh, où souvent on définit un pas d pour h=n×d, n∈ℕ et la tolérance δh=½d. Alors on peut estimer le variogramme par la formule : où n(h) est le nombre de paires de points dont l'interdistance est comprise entre h-δh et h+δh.
Dans un cas plus général, h pourra être un vecteur, et la somme se fera sur tous les points x, y tels que y=x+h. Cela permet de traiter les anisotropies.
Variogramme empirique d'un processus gaussien[modifier | modifier le code]
Si X est un processus gaussien, on peut estimer une loi du variogramme empirique.
Modélisation (ajustement)[modifier | modifier le code]
Le variogramme estimé n'est pas prédictif et ne respecte le plus souvent pas les contraintes de krigeage. C'est pourquoi les méthodes géostatistiques modélisent le variogramme estimé par une fonction continue soumise à certaines contraintes (fonction conditionnellement définie négative). Cette étape s'appelle la modélisation ou l'ajustement du variogramme. La modélisation est la partie essentielle du krigeage.
Modèle gigogne[modifier | modifier le code]
Le modèle est une fonction continue reproduisant au mieux l'allure générale du variogramme théorique. Toutes les fonctions ne sont pas possibles : elle doivent permettre la combinaison linéaire autorisée. Une combinaison linéaire ∑i λiZi est dite autorisée si son espérance et sa variance sont toujours définies (dans le modèle en question). On utilise généralement un modèle gigogne de variogramme sous la forme γ(h)=∑i γi(h). L'approche en modèle gigogne peut conduire à considérer le phénomène étudié comme une somme de fonctions aléatoires indépendantes, que l'on peut étudier séparément dans le cadre de l'analyse krigeante ; cependant, ces composantes n'ont généralement pas de signification physique propre.
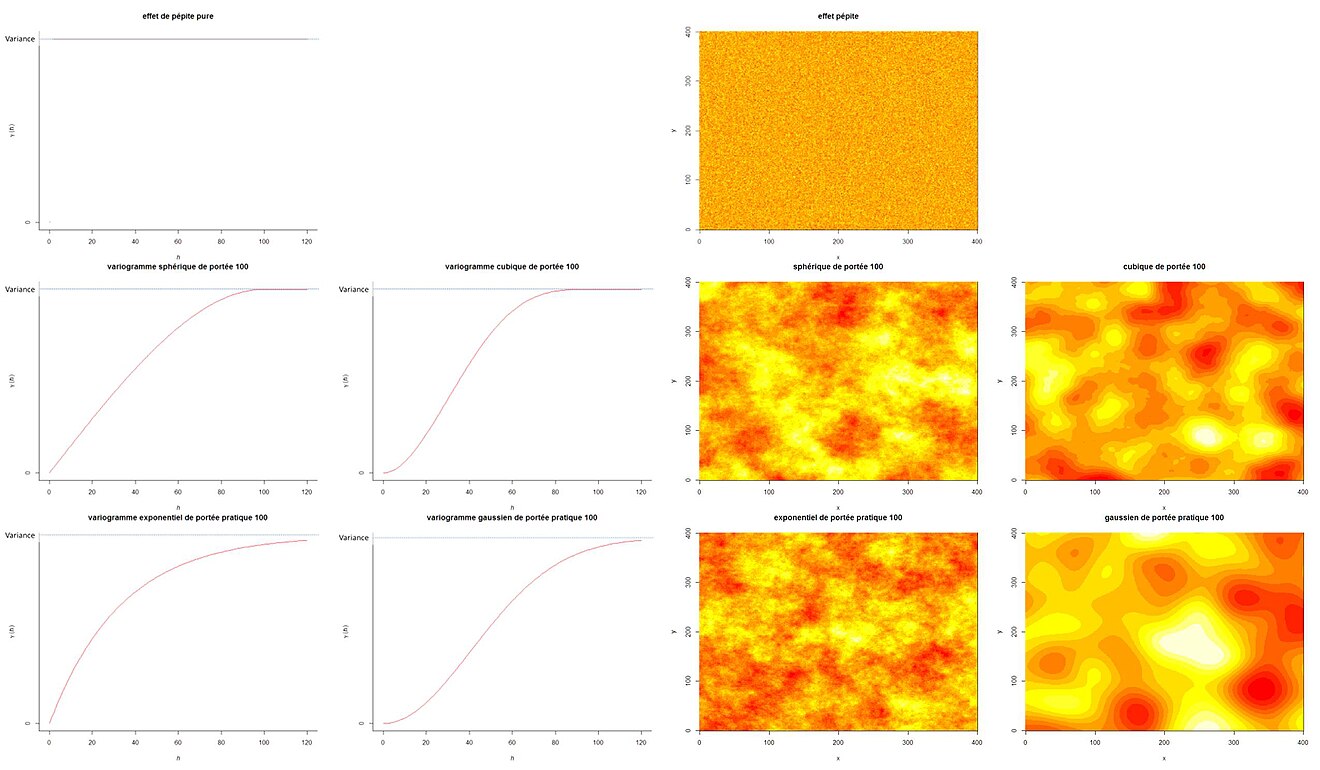
Les composantes sont définies par un palier C et éventuellement une portée a et des paramètres de formes. Les composantes γi les plus fréquemment utilisées sont :
| Comportement | Nom | Norme δ | Formule de la composanteγ(h) |
|---|---|---|---|
| composantes à palier C, sans portée | pépite pure (correspondant à un bruit blanc faible) | — | |
| composantes classiques à palier C et portée a | gaussien | 1,731 | |
| cubique | 1 | ||
| exponentiel | ≃ 2,996 | ||
| sphérique en dimension au plus 3[1] | 1 | ||
| sinus cardinal[2] | ≃ 20,371 | ||
| composantes classiques non-stationnaires | linéaire | 1 | |
| puissance[3] | 1 | ||
| composantes plus rarement utilisées | stable ou exponentiel généralisé | α√3 | |
| gamma | α√20-1 | , α>0 | |
| J de Bessel | 1 | , α>d⁄2-1 | |
| K de Bessel ou Matérn où Kα est la fonction de Bessel modifiée de deuxième espèce de paramètre α | 1 | , α>0 | |
| cosinus exponentiel, ou modèle à effet de trou[réf. nécessaire] | |||
| Cauchy généralisé | √(α√20-1) | , α>0 |
Anisotropie[modifier | modifier le code]
Le variogramme directionnel dans la direction d'un vecteur unitaire u est défini par γu(h) = ½Var[Z(x+hu)−Z(x)]. On parle d'anisotropie s'il existe deux vecteurs unitaires tels que les variogrammes directionnels sont différents. On distingue deux cas de figures principaux :
- anisotropie géométrique : portées différentes, même palier selon la direction ; le variogramme est une déformation linéaire A d'un variogramme isotrope γ0 ; γ(h) = γ0(‖Ah‖).
- anisotropie zonale ou stratifiée : même portée, paliers différents selon la direction ; le variogramme est somme de composantes présentant des anisotropies de supports : dans une certaine base, elles ne dépendent que de certaines coordonnées. Il est déconseillé d'utiliser des modèles où les anisotropies sont séparables selon les coordonnées (par exemple γ(h) = γ1(h1,h2) + γ2(h3))
Propriétés[modifier | modifier le code]
Le variogramme est une fonction paire, à valeurs positives.
Lorsque la covariance C est définie, elle est liée au variogramme par la relation :
où C(η) est la covariance à une distance η (dépendante uniquement de η pour une fonction aléatoire stationnaire)
Le variogramme est souvent une fonction croissante bornée. Dans ce cas, on nomme palier la limite du variogramme à l'infini et portée la distance où le palier est quasiment atteint (généralement, à 95 %). Lorsqu'elle existe, la variance C(0) est ce palier. En pratique, à cause en particulier des effets de bords, le variogramme calculé est croissant jusqu'à un maximum, puis globalement légèrement décroissant ou stable.
Convolution : soit Z la convolution p d'une fonction aléatoire Y : Z=Y∗p. Alors la relation entre leurs variogrammes vérifie γY=γZ∗(p∗p).
Propriétés du variogramme stationnaire[modifier | modifier le code]
- symétrie :
- -γ est de type positif conditionnel : soit une mesure λ vérifiant ∫λ(dt)=0, alors
- Pour tout t>0, e-tγ est une covariance
- le rapport γ(h)∕|h|2 est borné pour h⟶∞
- en l'absence de dérive, c'est-à-dire dans le cas intrinsèque, , autrement dit :
- si le variogramme est borné à l'infini, la fonction aléatoire est stationnaire d'ordre 2 ; il existe alors une covariance stationnaire C(h) telle que γ(h)=C(0)-C(h)
- Le variogramme γ(h) est égal à la demie variance d'extension d'un point {x} quelconque au point {x+h}
Le comportement à l'origine du variogramme traduit la régularité de la fonction aléatoire.
Autre présentation du variogramme[modifier | modifier le code]
On peut définir également le variogramme comme la fonction γ telle que
Cette formule fournit une définition du variogramme à une constante additive près.
Substitution entre variogramme et covariance[modifier | modifier le code]
Les formules définies dans l'hypothèse stationnaire peuvent être réécrites dans l'hypothèse intrinsèque, à condition qu'elles fassent intervenir des CLA, en remplaçant la covariance C par l'opposé du variogramme −γ
Effet pépite[modifier | modifier le code]
La formule fournit immédiatement γ(0)=0. Or l'on observe généralement que le variogramme ne tend pas vers 0 pour des petites distances. On appellera pépite la limite du variogramme en zéro. Elle représente la variation entre deux mesures effectuées à des emplacements infiniment proches, et peut donc provenir de trois effets :
- une variabilité naturelle du paramètre mesuré : il pourra par exemple prendre deux valeurs différentes si mesuré à deux instants différents ;
- une variabilité de l'instrument de mesure : la pépite mesure donc en partie l'erreur statistique de l'instrument de mesure ;
- un réel effet pépite : une variation brutale du paramètre mesuré ; le cas historique est le passage sans transition d'une pépite d'or à un sol ne contenant quasiment pas d'or.
Si le variogramme d'un champ est continu partout sauf à l'origine, ce champ se décompose en somme de deux champs, non-corrélés, de variogrammes respectifs une pépite pure et une fonction continue partout.
Cas multivariable[modifier | modifier le code]
En géostatistique multivariable est défini le variogramme croisé γ d'une fonction aléatoire multivariable intrinsèque Z = (Z(x,1); Z(x,2) ; … ; Z(x,n)) sur ses variables i et j au pas h : On pose sa généralisation γ̃ aux points x et y aux distances a et b : En toute généralité, γ n'est pas suffisant pour traiter le problème multivariable. Cette fonction est paire, donc ne rend pas compte des décalages entre variables. Précisément: Cela a conduit à introduire le pseudovariogramme croisé, qui a l'inconvénient de sommer selon des composantes différentes (donc potentiellement selon des unités différentes):
Articles connexes[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
 Pierre Chauvet, Aide-mémoire de géostatistique linéaire, Paris, Les Presses de l'École des Mines, (réimpr. 1993, 1994, 1998, 1999, 2008) (1re éd. 1989), 367 p., 16 × 24 cm (ISBN 2-911762-16-9, BNF 37051458)
Pierre Chauvet, Aide-mémoire de géostatistique linéaire, Paris, Les Presses de l'École des Mines, (réimpr. 1993, 1994, 1998, 1999, 2008) (1re éd. 1989), 367 p., 16 × 24 cm (ISBN 2-911762-16-9, BNF 37051458)
Références[modifier | modifier le code]
- nommé ainsi car il s'applique décompte de points d'un processus ponctuel de Poisson dans une sphère
- autorisé au plus à 3 dimensions ; atteint son palier la première fois à πa
- c'est le seul modèle autosimilaire, c'est-à-dire invariant par changement d'échelle : γ(k h) = kbγ(h) ; le phénomène spatial associé est sans échelle

![{\displaystyle \gamma (x,y)={\frac {1}{2}}\mathbf {Var} \left[Z\left(x\right)-Z\left(y\right)\right]={\frac {1}{2}}\mathbf {E} \left[|Z(x)-Z(y)|^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36da978d7b397481fa5988d8957b45639f3b0c58)
![{\displaystyle \gamma (h)={\frac {1}{2}}\mathbf {E} _{|y-x|=h}\left[|Z(x)-Z(y)|^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cd8d5d58a28c04ca9425f4630d564191caca9aa)


![{\displaystyle {\begin{aligned}&{\text{si }}X\sim {\mathcal {N}}_{n}(0,\Sigma )\\&{\text{alors }}{\hat {\gamma }}\left(h\right)\sim \sum _{i=1}^{\operatorname {n} \left(h\right)}\lambda _{i}\left(h\right)\chi _{i1}^{2}{\text{ pour des }}\chi ^{2}{\text{ iid à 1 ddl}}\\&{\text{soit }}\mathbf {E} \left[{\hat {\gamma }}\left(h\right)\right]=\operatorname {Trace} \left(A\left(h\right)\Sigma \right){\text{, }}\mathbf {Var} \left[{\hat {\gamma }}\left(h\right)\right]=2\operatorname {Trace} \left(A\left(h\right)\Sigma \right)^{2}\\&{\text{où }}A_{x_{i},x_{j}}=-{\frac {1}{\operatorname {n} \left(h\right)}}{\text{ si }}x_{i}\neq x_{j}{\text{, }}A_{x_{i},x_{i}}=-{\frac {\operatorname {n} \left(h\right)-1}{\operatorname {n} \left(h\right)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e665500c78a28917456d809531424c29c3bb75a9)




















![{\displaystyle \scriptstyle {\text{si }}\sum _{i}\lambda _{i}=0{\text{, alors }}\mathbf {Var} \left[\sum _{i}\lambda _{i}Z_{i}\right]=\sum _{i,j}-\lambda _{i}\gamma _{i,j}\lambda _{j}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fae1195d34419234047804c53823c59b13f9292)
![{\displaystyle \gamma _{i,j}\left(h\right)={\frac {1}{2}}\mathbf {Cov} \left[Z\left(x+h,i\right)-Z\left(x,i\right),Z\left(x+h,j\right)-Z\left(x,j\right)\right]\ \forall x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ab1b1e9e21bb125086e9f6794fc02c6fd3715d6)
![{\displaystyle {\tilde {\gamma }}_{i,j}\left(a,b\right)={\frac {1}{2}}\mathbf {Cov} \left[Z\left(x+a,i\right)-Z\left(x,i\right),Z\left(y+b,j\right)-Z\left(y,j\right)\right]\ \forall x,y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6de012f2883fa6a870ede66a26b88751ed83a80c)

![{\displaystyle \pi _{i,j}\left(h\right)={\frac {1}{2}}\mathbf {Var} \left[Z\left(x+h,i\right)-Z\left(x,j\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf73c7ea94446d704f47a6cc2f2bf5532bd9bdd4)