Utilisateur:Dsuchet phys20/Cerenkov
Explication du phénomène[modifier | modifier le code]

Dans un milieu matériel, la lumière se déplace à une vitesse , où est la vitesse de la lumière dans le vide et est l'indice de réfraction du milieu du milieu. Une particule chargée peut se déplacer dans ce milieu à une vitesse v supérieure à c1. La particule chargée interagit, tout au long de sa trajectoire, avec le milieu qu'elle traverse en perturbant temporairement la polarisation des couches électroniques des atomes rencontrés, ce qui provoque une émission radiative. Chaque atome rencontré par la particule devient donc émetteur d'un rayonnement à son passage. Or l'onde émise se propage à la vitesse c1 inférieure à v. L'interférence des ondes émises par chaque atome perturbé est alors constructive ; un front d'onde cohérent apparaît sous la forme d'un cône de lumière. La fréquence de cette onde constructive correspond généralement, pour l'effet Cherenkov dans l'eau, à celle du bleu ou de l'ultraviolet.
L’analogie entre l’effet Čerenkov et l'onde de choc est facile à faire. Un avion se déplaçant plus vite que le son dans l’air crée une onde de choc sur laquelle toutes les ondes sonores se retrouvent. La correspondance avec l’effet Cherenkov se fait en remplaçant l’avion assimilé à un point par une particule chargée et le son par la lumière. L'étude du nombre de Mach fournit cadre de pensée qui est directement applicable ici.
Explication de l'ouverture angulaire du phénomène[modifier | modifier le code]
Le rayonnement de la particule est émis dans un cône centré sur la trajectoire et caractérisé par son ouverture angulaire
Deux démonstrations de cette formule sont possibles. Pour chacune d'elle, on utilisera les hypothèses suivantes :
- La particule se déplace toujours dans la même direction (pas de diffusion sur les molécules du milieu) et à vitesse v constante (on ne prend pas en compte la perte d'énergie par rayonnement).
- On considère le rayonnement d'une longueur de la trajectoire de la particule, où est la longueur d'onde du rayonnement émis.
- On considère l'onde émise en chaque point comme une onde sphérique de pulsation . On pourra éventuellement se ramener à des ondes plus complexes par transformation de Fourier grâce à la linéarité des équations de Maxwell.
- On ne tient pas compte de la diminution d'amplitude due à la distance.
- Chaque point commence à rayonner avec une phase nulle au moment où l'électron passe en ce point.
Première démonstration[modifier | modifier le code]

On se place dans les conditions de Fraunhofer (l'observateur M est situé à l'infini) pour déterminer l'amplitude rayonnée dans la direction . Pour ce faire, il nous faut additioner les contributions de chaque point P de la trajectoire.
Prenons un point O de référence au centre de la trace. Quitte à changer l'origine des temps, on peut considérer que l'élément de trace autour de O commence à rayonner à l'instant donc qu'il émet une onde
.
Sa contribution au point M s'écrit donc
.
On ne tient pas compte de la diminution d'amplitude due à la propagation des ondes sphériques, car dans les conditions de Franhoffer le point M est situé à une distance de la trajectoire et la diminution est la même pour chaque point émetteur.
L'élément de trajectoire situé au point P , à une distance x du point O , commence à rayonner à l'instant
.
Il émet donc une onde dont l'amplitude est
et sa contribution au point M peut s'écrire
.
En sommant toutes les contributions et en utilisant la loi du retour inverse et le théorème de Malus pour déterminer la différence de marche entre les différents chemins, on obtient l'amplitude rayonnée dans la direction :
où représente la différence de marche .
On en déduit
où . En considérant l'intensité comme la valeur moyenne temporelle du carré du module de l'amplitude sur un grand nombre de période et en notant l'intensité émise par l'ensemble de la trajectoire, on trouve
Avec , la fonction est assimilable à la fonction de Dirac . Dans cette limite, on obtient la condition Čerenkov :
Seconde démonstration[modifier | modifier le code]
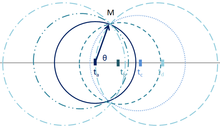
On peut mener un second type de raisonnement, plus qualitatif, pour comprendre la valeur de l'angle d'ouverture du cône de rayonnement. Ce raisonnement s'appuie sur les arguments développés par Richard Feynman dans son livre Lumière et Matière[1].
En tout point M de l'espace se superposent les ondes issues de chaque point de la trace. Toutes ces ondes présentent des phases différentes, qui dépendent à la fois de leur instant d'émission et de leur propagation jusqu'au point M. Pour chacun de ces points on peut trouver un point x' qui fournit un signal en opposition de phase au premier tant et si bien que leur somme s'annule. Il existe pourtant un point tel que les contributions de tous les points autour de ont la même phase et s'additionnent constructivement. Ce point est caractérisé par . Or, en prenant l'origine des phases à l'aplomb du point M (comme sur la figure ci-contre), on a
La condition se traduit alors par
Spectre du rayonnement Čerenkov[modifier | modifier le code]
Le spectre rayonné par la particule chargée lors de son mouvement a été déterminé pour la première fois par Ilia Frank et Igor Tamm en 1937. Elle leur a valu, avec Pavel Čerenkov, le prix Nobel en 1958 pour la découverte et l'interprétation de l'effet Čerenkov [2]. La formule de Frank-Tamm donne l'énergie rayonnée par une longueur de trace entre et
Notes et références[modifier | modifier le code]
- R. Feynman, Lumière et matière, Editions Seuil, (ISBN 2020147580), chapitre 3.
- http://www.nobelprize.org/nobel_prizes/physics/laureates/1958/index.html
(en) J. V. Jelley, Cerenkov Radiation and Its Applications, London, Pergamon Press,












![{\displaystyle s(O,M,t)=s_{0}\mathrm {d} x\,e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}\left[OM\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9037a7b8e83baa9da775b2bff76cabda96d86892)



![{\displaystyle s(P,M,t)=s_{0}\mathrm {d} x\,e^{-i\omega \left(t-{\frac {x}{v}}\right)}e^{i{\frac {2\pi }{\lambda }}[PM]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/962a812edde625d91aa598286371d4100e21de39)
![{\displaystyle S(\theta )=\int _{-L/2}^{L/2}s_{0}\mathrm {d} x\,e^{-i\omega \left(t-{\frac {x}{v}}\right)}e^{i{\frac {2\pi }{\lambda }}[PM]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e0932ea8606f6461b3d15704466fa4f321fea0)
![{\displaystyle =s_{0}e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}[OM]}\int _{-L/2}^{L/2}dx\,e^{-i{\frac {2\pi c}{\lambda }}{\frac {x}{v}}}e^{i{\frac {2\pi }{\lambda }}\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4acd0cbbbdca0be252df997f4a6b2d308ce53be9)

![{\displaystyle \delta =[PM]-[OM]=[P'O]=n\,x\,\cos \theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/102fead50e7623452b055d5d5ac3f760c65d262d)
![{\displaystyle S(\theta )=s_{0}e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}[OM]}\int _{-L/2}^{L/2}dx\,e^{i{\frac {2\pi }{\lambda }}\left(n\cos \theta -{\frac {c}{v}}\right)x}=s_{0}{\frac {L}{2}}e^{-i\omega t}e^{i{\frac {2\pi }{\lambda }}[OM]}sinc\left({\frac {\pi L}{\lambda }}\left(n\cos \theta -{\frac {c}{v}}\right)\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebe4f5b21c9a667c6049566a9b15ff010e474c8d)









![{\displaystyle \left.{\frac {\partial \varphi }{\partial x}}\right]_{x_{0}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6dd086472eaa23a88b08e75fa0cb3e8fcb0b184)





