Selle de singe

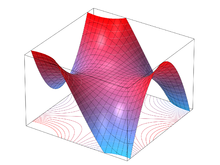
En mathématiques, la selle de singe est la surface définie par l’équation

z=x^{3}-3xy^{2}

.

Elle appartient aux surfaces en forme de selle (en) et son nom vient du fait qu'une selle pour un singe nécessite trois creux : deux pour les jambes et un pour la queue. Le point (0,0,0) sur la selle de singe correspond au point critique dégénéré de la fonction z(x, y) en (0, 0). La selle de singe a un ombilic isolé avec une courbure de Gauss nulle à l'origine alors que la courbure est strictement négative pour tous les autres points.

Pour montrer que la selle de singe a trois creux, on observe que l'équation ci-dessus peut s'écrire aussi $z(x,y)=\operatorname {Re} (x+\mathrm {i} y)^{3}$ .

Il en découle que z(tx, ty) = t³ z(x, y). En paramétrant cela par e^iφ, avec φ ∈ [0, 2π[, on voit que sur le cercle unité z(φ) = cos 3φ, donc z a trois creux. En remplaçant 3 par n'importe quel entier k ≥ 1 on peut créer une selle avec k creux.