Méthodes de mesure et d’analyse des paramètres démographiques des populations animales

Les méthodes d’inventaire et de mesures des paramètres démographiques des populations animales constituent des outils essentiels pour les écologues spécialistes de la gestion et de la Biologie de la conservation.

Elles leur permettent de les renseigner sur l’abondance de la population, son taux de croissance, les taux de survies et de fécondité, ainsi que les taux de dispersion (immigration et émigration). Ces méthodes sont employées dans un domaine de l’écologie nommé plus couramment en anglais wildlife techniques ou wildlife management, et ont connu des avancées spectaculaires au cours de ces 30 dernières années .

Parmi ces méthodes, le capture-marquage-recapture, le dénombrement direct ou encore les captures par unités d’efforts constituent quelques exemples d’outils fréquemment utilisés lors de la mesure des paramètres démographiques.

Définitions et contexte

Connaître le nombre d’individus, les paramètres démographiques et la structure (taille, âge-ratio, sexe-ratio, etc.) d’une population représente les premiers aspects à définir lors de l’analyse de celle-ci. Cependant, avant de pouvoir s’intéresser aux méthodes permettant de les mesurer, il est nécessaire d’être familiarisé avec certains termes employés par les écologues.

Dans un premier temps, il convient donc de définir ce qu’est une population. La population constitue un ensemble d’individus appartenant à la même espèce, vivant au même endroit à un temps « t » donné.

Associée à cette notion nous avons l’expression dynamique des populations. Elle correspond aux variations dans le temps et l’espace de la taille N d’une population (c’est-à-dire le nombre d’individus) en fonction des paramètres de croissance (soit la natalité et l’immigration) et de décroissance (soit la mortalité et l’émigration). Ces mêmes paramètres constituent un ensemble nommé paramètres démographiques, définis le plus souvent sous forme de taux (compris entre 0 et 1). Au cours d’un pas de temps t donné (généralement 1 an), la natalité (ou fécondité) correspond au nombre de nouveau-nés par individu reproducteur, la survie correspond au nombre d’individus survivant d’une année à l’autre (soit 1 – la mortalité), l’immigration correspond au nombre de nouveaux individus provenant d’autres populations et enfin l’émigration au nombre d’individus quittant la population.

Mesurer ces différents paramètres est une tâche difficile : tous les facteurs régissant la dynamique d’une population ne sont pas nécessairement connus et les jeux de données sont souvent incomplets, ce qui force les chercheurs à modéliser la population avec des connaissances incomplètes.

Cependant, la mesure de ces différents paramètres constitue une première étape indispensable à franchir lorsque l’on réalise des analyses de viabilité. Elles permettent de dresser un portrait global de l’état d’une population et prennent d’autant plus d’importance lors de la réalisation d’un plan de conservation ou de gestion. Si nous considérions une population en risque d’extinction, nous pourrions nous poser les questions suivantes : doit-on cibler la survie des plus jeunes individus ou celles des adultes ? Ou bien cibler la fécondité des individus reproducteurs ? Dans ce contexte, les méthodes de mesures des paramètres démographiques deviennent vitales pour répondre à ce genre de questions.

Méthodes d’estimations d’abondances d’une population

Pourquoi est-il nécessaire de connaître en premier lieu le niveau d’une population ? Les taux de survie ou de fécondité ne pouvant être déterminés avant de connaître le nombre d’individus, il faut d’abord avoir une bonne connaissance de son abondance, en particulier lorsqu'on souhaite l’exploiter (maintenir un effectif tout en prélevant des individus), la conserver (accroître son abondance, et, ou, empêcher son déclin) ou encore la contrôler (réduire une surpopulation).

Il existe de nombreuses méthodes permettant d’estimer le niveau d’une population, mais il ne sera décrit ici que celles qui sont fréquemment utilisées en gestion. Afin d’obtenir une liste plus exhaustive, il est conseillé de consulter des livres spécialisés.

Capture-marquage-recapture

Novisuccinea chittenangoensis (en), un rare escargot du Comté de Madison (New York) marqué pour étude.

La méthode de capture-marquage-recapture (CMR) est considérée comme la méthode classique pour déterminer l’abondance d’une population. Cette méthode est représentée par plusieurs modèles qui fournissent des estimations précises et peu biaisées.

Les principes de base sont les suivants :

• Les individus d’une population sont capturés afin d’être marqués pour une reconnaissance lors d’une éventuelle recapture ultérieure. Après marquage, les individus sont relâchés.
• La séance de capture ou « occasion de capture » est effectuée au minimum à deux reprises. À noter que les captures peuvent être remplacées par des observations.
• À chaque occasion de capture, les individus non-marqués capturés sont marqués, et le nombre d’individus marqués est noté.

La méthode de CMR constitue un échantillonnage, c’est-à-dire que les individus marqués ne constituent pas la totalité de la population. Ainsi, plus le nombre d'individus marqué est important, plus l’estimation d’abondance sera précise.

Il existe deux types de modèles de CMR : ceux pour les populations fermées et ceux pour les populations ouvertes.

Modèle de Lincoln-Petersen

Ce modèle ne s’applique que pour une population fermée, c'est-à-dire sans naissance, mort, immigration ou émigration au sein de la population. Afin de respecter cette prémisse, il faut réduire le temps entre les échantillonnages afin d’éviter l’ajout ou la soustraction d’individu, ce qui baisserait l’estimation d’abondance.

Principe :

• Le modèle de Lincoln-Petersen ne fait intervenir que deux occasions de captures.
• Un échantillon de M individu est constitué sur une courte période lors d’une première occasion de capture : ils sont capturés, marqués puis relâchés.
• Après quelques jours, une recapture est réalisée : un deuxième échantillon de n individus est donc constitué afin de déterminer le nombre d’individus marqués à la première occasion de capture (noté m).

De plus, il existe une condition (ou prémisse) universelle que nous devons nous efforcer de respecter pour ce modèle (également applicable à tous les autres modèles de CMR) : la proportion d’individus marqués par rapport aux individus non marqués est la même dans l’échantillon que dans la population.

L’estimation de la population est calculée de la manière suivante :

${\frac {M}{\hat {N}}}={\frac {m}{n}}\Leftrightarrow {\hat {N}}={\frac {M\times n}{m}}$

Cette formule est nommée indice ou index de Lincoln-Petersen (en).

Nous devons avoir, associé à toute estimation d’abondance, un intervalle de confiance (IC) représentant l’intervalle de valeurs ou l’étendue de valeurs que peut prendre le paramètre (ici l’abondance). Par exemple, si nous utilisons un IC à 95 %, il y a 95 % de chances que la valeur du paramètre soit contenue dans cet intervalle. Si nous supposons une distribution normale, l’IC à 95 % est environ égal à ± 1,96 erreurs-types (ET).

Le calcul d’une erreur-type est le suivant :

$ET={\sqrt {\frac {(m^{2}n)+(n-m)}{m^{3}}}}$

D’où l'intervalle de confiance :

$IC95\%({\hat {N}})={\hat {N}}\pm 1,96\times ET$

D’autres modèles pour populations fermées existent mais avec des occasions de capture supérieures à 2, comme le modèle de Schnabel ou d’Overton.

Modèle de Jolly-Seber

Ce modèle s’applique sur une population ouverte : les variations de l’effectif sont soumises aussi bien aux naissances et aux décès d’individus, qu’aux individus arrivant dans la population (immigrants) et ceux qui la quittent (émigrants). En plus d’estimer l’abondance d’une population, elle permet également de déterminer les taux de survie et de fécondité (voir article plus en dessous).

Principe :

• Trois occasions de captures, au minimum, sont réalisées.
• À chaque occasion, les individus marqués sont comptés, ceux non marqués sont marqués puis tous les individus sont relâchés.
• L’estimation d’abondance est égale à la quantité d’individus marqués divisés par la proportion d’individus marqués.

Les prémisses du modèle de Jolly-Seber à respecter sont les suivantes :

• Tous les individus ont la même probabilité de capture.
• Tous les individus marqués ont les mêmes probabilités de survie.
• Les marques doivent être permanentes.
• Chaque échantillonnage est instantané et les individus sont directement relâchés une fois marqué.
• Chaque individu a la même probabilité d’émigrer, et toute émigration est définitive.

Dans un premier temps, il est nécessaire de connaître la proportion d’individus marqués à la période t :

${\hat {a}}_{t}={\frac {m_{t}+1}{n_{t}+1}}$

Avec :

• m(t) = nombre d’individus préalablement marqués, capturés dans l’échantillon t.
• u(t) = nombre d’individus non marqués capturés dans l’échantillon t.
• n(t) = m(t) + u(t) = nombre d’individus total capturé dans l’échantillon t.

Dans un second temps, nous calculons le nombre d’individus marqués M(t) à la période t :

$M_{t}={\frac {(s_{t}+1)Z_{t}}{R_{t}+1}}+m_{t}$

Avec :

• S(t) = nombre d’individus relâchés après l’échantillon t = n(t) – (nombre d’individus morts).
• R(t) = nombre de S(t) relâchés au temps t, pouvant être capturés ultérieurement.
• Z(t) = nombre d’individus capturés avant l’échantillon t qui ne sont pas capturés dans l’échantillon t mais qui le seront plus tard.

Enfin, celle-ci nous permet d’estimer l’abondance de la population :

${\hat {N}}={\frac {M_{t}}{{\hat {a}}_{t}}}$

Dénombrement total

Le dénombrement total correspond à un comptage de la totalité du nombre d’individus dans une population. L’échantillonnage et les calculs statistiques ne sont donc pas nécessaires. Il existe peu de situations dans lesquelles ces méthodes sont réalisables, car dès que la zone d’étude est trop grande, la détectabilité diminue. Il est donc indispensable d’être prudent lors de leur utilisation car il y a toujours une possibilité que certains individus soient dissimulés ou tout simplement manqués par les observateurs. Si cela arrive, il n’existe aucun moyen pour détecter un biais dans l’estimation d’abondance. C’est pour cela qu’il faut demeurer sceptique et les utiliser plutôt comme des indices.

L’avantage de ces méthodes est qu’elles sont non-invasives, contrairement aux méthodes de CMR.

Dénombrement par véhicule(s)

Paysage de savane au Kenya.

La prémisse de cette méthode est qu’elle n’est qu’applicable que lorsque l’habitat est ouvert et que les individus sont bien visibles (par exemple une savane dégagée).

Plusieurs véhicules sont espacés d’une certaine distance et avancent à la même vitesse le long d’une ligne de départ traversant la zone d’étude (ou transect). Les distances, la vitesse et la zone d’études sont préalablement identifiées. Les observateurs doivent compter uniquement le nombre d’individus situés à leur droite, afin d’éviter que des individus ne soient comptés deux fois. Si des individus sont capables de sortir de la zone d’étude, des observateurs doivent être postés à ses limites.

Dénombrement par photographie aérienne

L’ensemble présumé de la population est photographié. Le dénombrement se fait par simple comptage du nombre d’individus sur les photographies. Cependant, les estimations peuvent être hautement biaisées lorsque des individus sont cachés sous l’eau ou sous des arbres (indétectables par la photographie).

Dénombrement par « Spot Mapping »

Cette méthode est efficace avec les oiseaux. On effectue une cartographie sur laquelle sont représentés des regroupements d’individus. Lors de la reproduction, on suppose que ces regroupements correspondent à des centres d’activités et l’on peut ainsi dénombrer les individus.

Cependant, cette méthode suppose que :

• L’abondance de la population est constante pendant l’inventaire et que les individus occupent des territoires exclusifs.
• Le nombre d’individus par centre d’activité est précis.
• Les observateurs doivent être expérimentés et la prise de donnée rigoureuse.

Dénombrement total sur des parcelles d'échantillons

Le principe consiste à compter le nombre d’individus à l’intérieur d’une parcelle de surface prédéfinie disposée au hasard dans la surface d’étude. La prémisse stipule que tout individu observé à l’extérieur de la parcelle n’est pas compté. Ces parcelles sont plus généralement appelées transects. La ligne de transect traverse la parcelle et la découpe en deux parties d’égale largeur.

Nous calculons dans un premier temps la densité D dans la parcelle d’échantillonnage :

$D={\frac {\sum {x_{i}}}{\sum {a}}}$

Avec :

• x(i) = nombre d'individus observés dans la parcelle i.
• a = surface de la parcelle.

Le nombre d’individus dans la population est ensuite inféré à partir de la densité D :

${\hat {N}}=D\times A$

Avec : A = surface de l’aire d’étude.

En combinant les deux formules, nous obtenons :

${\hat {N}}={\frac {A\sum {x_{i}}}{2Lwn_{s}}}$

• L = Longueur du transect.
• w = largeur de la moitié de la parcelle.
• n(s) = nombre de parcelles.

La variance est ensuite calculée de la manière suivante :

$s_{x}^{2}={\frac {\sum {x_{i}^{2}-{\frac {(\sum {x_{i}})^{2}}{n_{s}}}}}{n_{s}-1}}$

L'erreur-type est calculée comme ceci :

$ET={\sqrt {\frac {s_{x}^{2}}{n_{s}}}}$

Ce qui nous permet finalement de calculer l'IC :

$IC95\%({\hat {N}})={\hat {N}}\pm 1,96(ET)$

Captures par unité d'effort (CPUE)

Effort variable

Les CPUE constituent un groupe de méthodes applicables lorsque le niveau d’exploitation est suffisant pour que le prélèvement réduise de manière appréciable les stocks d’individus. Ces méthodes sont souvent utilisées lors d’inventaires de populations de poisson d’eau douce. En effet, cette méthode est pratique lorsque la population est exploitée (comme dans le cadre de la pêche sportive). De plus les poissons peuvent être marqués avant d’être relâché (ce qui évite le retrait d’individu) : au cours des pêches ultérieures, les poissons marqués ne sont pas considérés. La prémisse sous-jacente à ces méthodes est que la capture d’animaux diminue leur disponibilité future et que le nombre de captures par unité d’effort^{[pas clair][Quoi ?]} diminue. Cependant, l’individu peut être vu ou entendu, un marquage peut être considéré comme un retrait de la population d’individus non marqués.

Les prémisses de cette méthode sont :

• Pour chaque période, la probabilité de capture est constante (donc la relation est linéaire).
• La population est fermée (à l’exception du retrait ; problème potentiel si la période de temps entre les inventaires est longue).
• Le nombre d’individus retirés est connu avec exactitude.

La méthode « traditionnelle » consiste à réaliser une régression du nombre de captures par unité d’effort en fonction du nombre de prises cumulées.

Régression du nombre de captures par unité d’effort en fonction du nombre de prises cumulées.

Méthode de Leslie

• y(i) = A + B(x(i))) équivaut au nombre de captures par unité d’effort
• A = l’ordonnée à l’origine de la droite y
• B = pente de la régression
• x(i) = nombre de captures cumulées
• N(0) = A/-B

Attention, la pente est négative, le –B rétablie une valeur positive.

Cependant, comme le nombre de captures par unité d’effort et la récolte sont recueillis en même temps, ces informations ne sont pas indépendantes et le calcul de la variance est imparfait. De plus, pour être efficaces et produire un estimé relativement exact, on doit prélever environ 70 à 80 % de la population (ce qui peut être dangereux pour elle).

Effort constant

Cette fois-ci l’effort est constant, c’est-à-dire que le temps de pêche par passage et que la superficie couverte restent constants. Il existe deux méthodes principales, la méthode de Zippin à trois séances de capture et la méthode de Seber - LeCren à deux séances de capture (non abordée ici).

La méthode de Zippin permet une estimation de l’effectif basée sur la capture d’individus qui ne sont pas relâchés et sur une procédure graphique suivie de la détermination précise de l’asymptote de l’estimateur.

Les prémisses sont les suivantes :

• L’effort de capture est constant.
• La probabilité de capture est constante entre les individus et d’une séance à l’autre (donc la relation est linéaire).
• La population est fermée (à l’exception du retrait, problème potentiel si la période de temps entre les inventaires est longue).

Nous devons tout d’abord calculer R qui est un paramètre nous permettant de vérifier la validité du test, avec R<1 pour qu’il soit valable.

$R=\sum _{i=1}^{S}\left({\frac {(i-1)c_{i}}{c}}\right)$

Avec :

• S(i) = nombre d’unités d’échantillonnage (nombre de séances)
• i = une unité d’échantillonnage (séance de capture) donnée.
• C(i) = nombre de captures pour l’unité d’échantillonnage i
• C = somme de toutes les captures.

L’estimation se calcule ainsi :

${\hat {N}}={\frac {c}{1-q^{s}}}$

Pour l'erreur-type :

${\begin{aligned}&ET={\sqrt {\frac {{\hat {N}}(1-{\hat {q}}^{s})({\hat {q}}^{s})}{(1-{\hat {q}}^{s})^{2}-({\hat {p}}s)^{2}{\hat {q}}^{s-1}}}}\\&\\&{\hat {q}}={\sqrt[{3}]{{\hat {q}}^{s}}}\;et\;{\hat {p}}+{\hat {q}}=1\end{aligned}}$

P et q sont des probabilités déterminées grâce à la valeur de R et trouvé avec l’aide de la table de Zippin. L’important est de savoir qu’ils nous permettent de calculer l’erreur type.

L’intervalle de confiance est ainsi donné par :

$IC95\%({\hat {N}})={\hat {N}}\pm 1,96\times ET$

Ce test est considéré comme valable si

$R<{\frac {s-1}{2}}$

• Plus les écarts sont grands entre le nombre de captures par séance, plus la valeur de R sera petite, et plus l’IC95% (et le pourcentage de variation) diminue.
• Plus les premières séances de captures sont efficaces, plus l’estimé de Zippin s’approche du nombre de capture (C).

Estimations des paramètres démographiques dans une population non-structurée

Population non-structurée

La dynamique des populations non-structurées désigne l’évolution de populations au sein desquelles l’identité des individus ainsi que leurs caractères phénotypiques ne sont pas pris en compte. Tous les individus sont considérés comme identiques du point de vue de leur âge, de leur survie ou de leur fécondité. Cette dynamique des populations non structurées se base sur deux modèles théoriques principaux : modèle « densité indépendance » et modèle « densité dépendance ».

Modèle exponentiel (ou de Malthus) : densité indépendance

Dans ce modèle est présumée une croissance de la population indépendante de la densité. Plus précisément, la croissance de la population est indépendante du caractère limitant des ressources. Même pour une densité d’individus N importante, la pression du milieu est absente ; les ressources ne limitent pas la croissance. Ainsi le taux de natalité et de mortalité de la population, et donc sa croissance, ne se trouvent pas affectés par la densité. La croissance est exponentielle : la population connait une explosion démographique, ce qui la met en propre danger pour la compétition des ressources.

Ce modèle est basé sur plusieurs prémisses essentielles :

• Pas de variabilité dans les paramètres.
• La population doit être égale à un nombre entier.
• La croissance exponentielle est à l’infini, donc il y a une disponibilité illimitée de ressources.
• La natalité ou la mortalité sont indépendantes de l’âge ou de la taille ; tous les individus sont identiques.
• Une seule population fermée, pas de sous-groupe structuré, tous les individus peuvent potentiellement se reproduire entre eux.
• La natalité et la mortalité surviennent durant une courte période.

Selon le modèle :

• N(t+1) = N(t)R + N(t)
• N(t+1) = N(t) x (R+1)
• N(t+1) = N(t) x ʎ
• N(t+2) = N(t+1) x ʎ
• N(t+2) = N(t) x ʎ x ʎ
• N(t+2) = N(t) x ʎ²

et donc N(t) = N(0) x ʎ^(t)

Avec :

• ʎ = taux vital densité indépendante = constante.
• R = taux intrinsèque d’accroissement de la population = natalité – mortalité + immigration – émigration.

Mais ici, compte tenu du modèle non structuré, R est un taux de natalité constant.

Ainsi, le nombre d’individus dans la population à l’année t (N(t)) est égal à la densité initiale (N(0)) multipliée par le nombre moyen de jeunes produits par individu à la puissance t (ʎ^(t)). Ces équations sont utilisées lorsque la natalité et la mortalité surviennent lors de périodes de temps très court (temps discret).

Lorsque la natalité et la mortalité surviennent en permanence (temps continu), on utilise une équation différentielle :

${\frac {dN}{dt}}=rN$

Avec :

• dN = variation du nombre d’individus.
• dt = le pas de temps infinitésimal
• r = le taux de croissance intrinsèque de la population = natalité – mortalité + immigration – émigration.

Courbe exponentielle en temps discret - Modèle de Malthus.

Modèle de Verhulst : Densité dépendance négative

Ce modèle, aussi caractéristique des populations non structurées, met en évidence une croissance de la population freinée par un manque de ressources. Au sein de ce modèle, les ressources (espace, eau, nourriture, etc.) sont limitées. Cela entraîne des compétitions entre individus, et donc une diminution de la survie et/ou de la fécondité de la population lorsque celle-ci atteint un nombre d’individus N trop élevé. Ainsi la croissance de la population devient dépendante de sa densité.

Ce modèle est basé sur plusieurs prémisses essentielles qui sont les mêmes que pour le modèle de Malthus, sauf que les ressources ne sont pas illimitées ce qui entraîne des phénomènes de compétition intraspécifique.

Selon le modèle de Verhulst, une population s'autocontrôle (incorporation de la densité dépendance négative) par compétition intraspécifique, dont il existe deux modes :

• La compétition par interférence ou par concours (« contest competition ») : il y a un partage inégal des ressources entre individus. Les individus dominants réussissent toujours à obtenir assez de ressources pour survivre et se reproduire.
• La compétition par exploitation (« scramble competition ») : il y a un partage plutôt égal des ressources entre individus. Mais à très forte densité, les ressources peuvent être insuffisantes pour subvenir au besoin des individus.

Selon ce modèle :

${\frac {dN}{dt}}=rN\color {green}{(1-{\frac {N}{K}})\rightarrow {\text{Coefficient de freinage}}}$

Avec :

• K = capacité de charge dans le milieu = nombre maximum d’individus que peut supporter l’environnement).
• dn/dt = la variation du nombre d’individus en fonction de la variation du temps = la croissance de la population.

Lorsque N = K alors dn/dt = 0, la population ne peut plus croître et atteint un plateau.

Courbe en temps continus - Modèle de Verhulst.

Courbe en temps discret - Modèle de Verhulst.

Courbe du Modèle « Scramble ». Si N(t) > K alors la population sera en décroissance (N(t+1) < N(t)).

Courbe du modèle « Contest ». Si N(t) > K alors la population sera en décroissance (N(t+1) < N(t)).

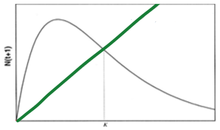
Estimation des paramètres démographiques

Estimation du taux de croissance R à partir d'un dénombrement

L’estimation du taux de croissance peut se calculer de différentes façons, mais la plus simple est d’utiliser l’équation de croissance logistique et de mettre en logarithme chacun des côtés de la formule, soit :

$\log(N_{t})=\log(N_{o})+R\times t$

La régression linéaire de log(N(t)) en fonction de t fournit le taux de croissance r (égal à la pente de la droite) et l’ordonnée à l’origine. Le nombre d’individus par unité de temps ne nécessite ainsi que de passer sous forme logarithmique.

Estimation du taux de croissance avec des changements d'abondance

Le modèle exponentiel fournit un autre moyen de calculer le taux de croissance r. Considérons des ratios successifs de taille de population en fonction du temps :

${\frac {N_{t}}{N_{t+1}}}={\frac {N_{0}e^{rt}}{N_{o}e^{r(t-1)}}}=e^{r}$

Le logarithme de la moyenne de ces ratios est ensuite utilisé pour estimer r. Cette méthode est cependant moins efficace et précise que la méthode précédente.

Estimation du taux de survie par les méthodes de CMR

Considérons une étude ayant J occasions de capture. Supposons ensuite que tous les individus aient la même probabilité ci d’être capturé à l’occasion i et la même probabilité de survivre Si (population non structurée) de l’occasion i à i+1. M(i) représente le nombre d’individus marqués à l’occasion i parmi N(i) (représentant l’abondance de la population à l’occasion i). De plus, à l’occasion i, ni individus sont capturés, parmi lesquels m(i) ceux déjà marqués et u(i) ceux qui ne sont pas encore marqués. R(i) correspondra au nombre d’individus parmi ces ni qui ont été relâchés après l’occasion i.

L’estimation du taux de survie Ŝ se calcule de la manière suivante :

${\begin{aligned}&{\hat {S}}_{i}={\frac {{\hat {M}}_{i+1}}{{\hat {M}}_{i}-m_{i}+R_{i}}}\\&\\&{\hat {M}}_{i}=m_{i}+{\frac {R_{i}z_{i}}{r_{i}}}\end{aligned}}$

Où z(i) = nombre d’individus capturé avant l’occasion i, mais capturé après l’occasion i (aucunement les individus capturés de l’occasion i).

Le modèle de Cormack-Jolly-Seber permet également de calculer des probabilités de survie φ entre t et t+1 :

$\varphi _{t}={\frac {{\hat {M}}_{t}}{{\hat {M}}_{t}+(s_{t}+m_{t})}}$

L’équation prend également en compte le fait que l’individu ne quitte pas la zone d’étude : c’est une probabilité de survie locale.

Estimation du taux de survie à partir d'observations

Suivi d'oiseaux par radiopistage dans une réserve de Nouvelle-Zélande.

Il est possible de calculer le taux de survie sans difficulté lorsqu’un suivi rigoureux et attentif est déjà en place, par exemple une population en captivité.

L’estimation du taux de survie dans certaines études peut être également simple tant que les individus marqués portent en permanence la marque et qu’ils peuvent être localisés. La radiotélémétrie offre cette possibilité dans laquelle les individus portent des émetteurs dont la traçabilité et la localisation sont faciles. Cependant, cela peut poser des problèmes lorsque les émetteurs sont défaillants, lorsque l’animal meurt sans que l’on ait la possibilité de retrouver (émetteur détruit, animal noyé), ou encore lorsque l’animal quitte la zone d’étude.

Estimations du taux de survie à partir de ratios de populations ou d'indices

S’il n’y a pas de phénomène de dispersion apparent dans la population, la mortalité peut être calculé de façon simple : la mortalité entre le temps t et t+1 correspondra à la taille de la population au temps t moins le nombre d’individus restant au temps t+1. Cependant, le nombre d’individus au temps t+1 (c’est-à-dire les survivants) doit distinguer les nouveau-nés des adultes.

Dans le cas où tous les individus de la population sont dénombrés (ce qui est rare), le taux de survie peut se calculer directement sans passer par la méthode précédemment citée. Par exemple, si nous observons 10 adultes et 4 jeunes au temps t, et qu’au temps t+1 nous n’observons plus que 10 de ces individus, nous pouvons alors poser :

$s={\frac {10}{14}}=0,71$

Les taux de survie peuvent ainsi être déterminés d’année en année.

Estimation du taux de fécondité à partir d'observations

Lorsqu’une observation de tous les individus est réalisable (ou un dénombrement total), le taux de fécondité peut facilement se mesurer en distinguant le nombre de jeunes présents avec les adultes. Il est également possible de le mesurer en regardant les cicatrices placentaires des mammifères femelles (comme le rat musqué par exemple), ou le nombre de jeunes par nid d’oiseau. Il faut cependant rester prudent en réalisant ces observations : il est tout à fait possible d’observer des adultes sans leurs jeunes, les cicatrices placentaires ne reflètent pas le nombre de jeunes qui ont survécu et les nids d’oiseaux présentant des jeunes peuvent être plus facilement trouvés.

Estimation du taux de recrutement à partir de CMR

Le modèle de Jolly-Seber permet de calculer le taux de recrutement, qui inclut à la fois le taux de natalité et le phénomène d’immigration. Il est défini comme le nombre de nouveaux individus au temps i par individu au temps i – 1.

$f_{i}={\frac {N_{i+1}-N_{i}\phi _{i}}{N_{i}}}$

Estimation des paramètres démographiques dans une population structurée

Population structurée

La dynamique des populations structurées désigne l’évolution de populations au sein desquelles l’identité des individus ainsi que leurs caractères phénotypiques sont pris en compte. Tous les individus sont considérés comme différents du point de vue de leur âge, de leur survie ou de leur fécondité. Cette dynamique des populations structurées se base sur un modèle d’étude principal qui est la matrice de Leslie.

Il existe dans ce modèle, non plus théorique, mais réaliste, plusieurs classes d’individus séparées par leur âge ou stade. Ces classes d’individus font partie intégrante d’un cycle de vie comportant différents taux (mortalité, survie, fécondité, croissance) spécifiques à chaque catégorie d’individus, et non plus commun à tous les individus de la population comme dans le cadre des populations non structurées.

Dans le cadre d’un cycle de vie, et à partir du nombre d’individus par classe et des différents taux de vie, il est possible de prédire le nombre d’individus à la génération suivante. Prenons un exemple simple d’une population végétale :

Exemple d'un cycle de vie classique.

Les prédictions pour chaque classe d’âge, ou de stade dans la population, du nombre d’individus à la génération suivante (N(t+1)) à partir de la génération actuelle (N(t)), vont être déduites comme tel :

• N0(t+1) = N0(t)S + N1(t)F1 + N2(t)F2 + N3(t)F3
• N1(t+1) = N0(t)S0
• N2(t+1) = N1(t)S1
• N3(t+1) = N2(t)S2

Ces calculs peuvent être représentés de façon matricielle au sein d’une matrice de Leslie tel que : Vecteur t+1 (V(t+1)) = M (matrice) x Vecteurs t (V(t))

Matrice de Leslie.

Estimation des paramètres démographiques

Estimation du taux de croissance d'une population à partir du taux de naissance et du taux de mortalité

Nous pouvons déduire le taux de recrutement de la mesure entre le nombre de jeunes femelles par rapport au nombre de femelles adultes (dans une période bien définie, par exemple un an). Avec le taux de survie et le taux de fécondité, nous pouvons estimer la moyenne du changement dans la population. Nous pouvons poser l’équation :

$A_{t+1}=A_{t}(S_{A_{t}})+Y_{t}(S_{Y_{t}})$

Avec :

• A(t) le nombre d’adultes femelles à l’année t.
• Y(t) le nombre de jeunes à l’année t.

Nous pouvons ajouter une équation avec le taux de recrutement :

$Y_{t}=A_{t}(R)$

Alors nous pouvons poser :

$A_{t+1}=A_{t}(S_{A_{t}})+A_{t}(S_{Y_{t}})(R)$

Nous avons ainsi :

$A_{t+1}=\lambda$

λ étant le taux de croissance de la population.

Estimation du taux de survie par suivie d'une cohorte

Supposons que nous connaissons l’intégralité de l’histoire de vie d’une cohorte qui s’étendrait sur q(n) classe d’âge. Alors le taux de mortalité q(0) serait :

$q_{0}={\frac {{\text{Nombre de survivant à }}q_{1}}{\text{Nombre d'individus initial dans la cohorte}}}$

Nous pouvons donc écrire :

$q_{n}={\frac {nb\;individu\;q_{n+1}}{nb\;individu\;q_{n}}}$

Il existe d’autres méthodes permettant d’extrapoler le nombre de morts durant l’année i par une variante binomiale, avec n(i) représentant le nombre d’animaux en vie au début de l’année par un taux = q(i), ainsi qu’une erreur standard pouvant lui être associé.

Après avoir suivi une cohorte à intervalle de temps régulier, nous pouvons par simple comptage identifier le nombre de morts dans la population (soit dans une population fermée, soit dans un groupe d’individus marqués représentatif). La survie S se calcule simplement par : S = 1 – M avec M mortalité

Si le suivi s’effectue sur plus d’une cohorte, une table âge-spécifique peut être générée pour chacune d’entre eux. Les taux de survies peuvent, par exemple, être générés à la fois pour l’âge et par année.

Estimation du taux de survie depuis les distributions par âge

Si nous ne connaissons pas l’ensemble des taux de mortalité dans une population (c’est-à-dire que le travail de suivi de cohorte n’a pas été effectué), mais que l’on connaît sa distribution par âge à un temps donné (par une méthode de recensement), nous pouvons monter une distribution par classe d’âge en supposant que cette population possède une distribution d’âge stable, avec une taille constante. Pour trouver les taux de mortalité et de survie, il suffit alors de procéder aux mêmes calculs que précédemment.

Chapman et Robson proposent une autre façon un peu plus rigoureuse pour calculer un taux de survie d’une population lorsque l’on possède une distribution par classe, et ce, avec une faible variance.

${\hat {S}}={\frac {T}{n+T-1}}$

Dans laquelle :

$n=\Sigma _{j\geq 1}n_{j}{\text{ et }}T=\Sigma _{j\geq 1}jn_{j}$

Avec :

• Ŝ = taux de survie annuel.
• n(j) = observation indépendante j
• T = la somme des X(i)
• X(i) = âge de l’individu i

Une erreur standard peut lui être associée :

$SE^{2}({\hat {s}})={\hat {s}}\left({\hat {s}}-{\frac {T-1}{n+T-2}}\right)$

Et donc pour l'écart-type :

${\text{Se}}={\sqrt {SE^{2}}}$

Toutefois Caswell met en garde : on présume au sein de ce modèle une distribution d’âge stable, alors qu’il existe des variations environnementales qui peuvent affecter les différentes classes d’âges, et souvent, cette stochasticité peut affecter différemment chaque classe d’âge.

Estimation du taux de fécondité net

Il s’agit d’un autre outil statistique pour déterminer le taux de fécondité net, qui est la moyenne du nombre de jeune produit par un individu durant sa vie :

$R_{0}=\sum l_{x}m_{x}$

Avec :

• l(x) = taux de survie.
• m(x) taux de fécondité.

Si R(0) < 1 alors la population décline, si R(0) > 1 la population croit et si R(0) = 1 alors la population est stable.

Cependant, comme dit précédemment, les résultats donnés par ces formules ne sont que des photos, c’est-à-dire une représentation de la réalité à un temps t. Elles ne prennent pas en compte la stochasticité environnementale, démographique, les interactions proie-prédateur, etc.

Estimation des taux de dispersion (Immigration et émigration)

La dispersion comprenant l’immigration et l’émigration, est un phénomène difficile à détecter et encore plus à mesurer. Généralement, l’écologue ignorera ces phénomènes (en effectuant par exemple des échantillonnages sur des temps très courts), ou espérera que l’immigration soit égale à l’émigration. Bien que la littérature sur la dispersion soit fournie, très peu d’attention a été portée aux méthodes permettant de la mesurer.

La détection et la mesure de ces mouvements se font typiquement grâce au marquage ou à l’observation des individus. Ceci permet de connaître la direction, la distance, le temps de résidence et le temps entre la capture et la recapture. Cependant, afin d’obtenir une estimation plus précise des mouvements, la radiotélémétrie s’avère indispensable. De plus, elle permet de s’intéresser aux domaines vitaux et les territoires des individus .

Bien que les méthodes de CMR soient conçues en tant qu’estimateurs de taille d’une population, il est possible de s’intéresser aux changements de taille par gain ou perte d’individus entre chaque occasion de capture. D’une part, Pollock et Nichols ont développé un modèle où ils distinguent l’immigration et la natalité dans les gains d’abondances.

D’autre part, Zeng et Brown ont développé un modèle où les pertes d’abondances sont distinguées entre la mortalité et l’émigration.