Grammaire d'arbres adjoints

La grammaire d'arbres adjoints, grammaire TAG, ou légèrement sensible au contexte, est un formalisme d'analyse grammaticale introduit par Aravind K. Joshi et ses collègues en 1975. Ce formalisme a été utilisé à différentes fins, et particulièrement en linguistique formelle et informatique pour le traitement de la syntaxe des langues naturelles. Historiquement, il a d'abord permis de représenter de manière directe des dépendances à longue distance et il permet également de représenter les dépendances croisées du suisse allemand et du flamand occidental, phénomène qui ne peut se traiter avec une grammaire de réécriture hors contexte, comme l'a montré S. Shieber. Finalement il permet de représenter aisément des grammaires dites fortement lexicalisées et appartient aux grammaires d'unifications.

Mis à part son usage pour la description syntaxique, les grammaires d'arbres adjoints ont aussi été utilisées à des fins de description linguistique pour représenter des structures sémantiques, de dialogue ou des structures synchrones. On trouve aussi des usages du formalisme en BioNLP.

Définition

Une Grammaire d'arbres adjoints (TAG) est un système de réécriture d'arbres composé :

• D'un ensemble de symboles non-terminaux, N.
• D'un ensemble de symboles terminaux, T, disjoint de N : T ∩ N = ∅.
• D'un élément distingué de N, appelé « Axiome » et noté S.
• D'un ensemble d'arbres initiaux (I) Un arbre initial est un arbre fini, muni d'un ordre linéaire, dont les nœuds feuille sont soit des symboles terminaux soit des symboles non terminaux, dans ce dernier cas ces nœuds sont appelés nœuds de substitution.
• D'un ensemble d'arbres auxiliaires (A) disjoint de I : A ∩ I = ∅. Les nœuds feuille d'un arbre auxiliaire sont étiquetés, soit par des symboles terminaux, soit par des symboles non terminaux. Un arbre auxiliaire comporte exactement un nœud feuille étiqueté par un symbole non terminal appelé « nœud pied ». Le nœud pied et la racine de l'arbre auxiliaire sont nécessairement de même catégorie. Tout autre nœud étiqueté par un non terminal est appelé « nœud de substitution ».

Par convention, on appelle arbres élémentaires la réunion des ensembles I et A. On appelle également ancres les nœuds terminaux des arbres élémentaires. Il est commode d'adresser les nœuds en utilisant la convention de Gorn. Toujours par convention, on note les nœuds de substitution avec une flèche orientée vers le bas et les nœuds pieds avec une étoile.

Une grammaire d'arbres adjoints est munie de deux opérations de composition, l'adjonction et la substitution.

• Substitution : Soient α et β deux arbres élémentaires, la substitution de α à l'adresse x de β consiste à remplacer le nœud de substitution s d'adresse x de β par le nœud r racine de α. La substitution est autorisée uniquement si r et s sont étiquetés par un symbole identique.

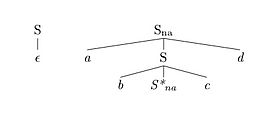
• Adjonction : Soient β un arbre élémentaire et γ un arbre auxiliaire, on adjoint γ sur le nœud x de β en découpant β en deux parties. Le nœud x situé dans la partie supérieure (top) de β est remplacé par la racine de γ, le nœud x racine de la partie inférieure (bottom) de β est remplacé par le nœud pied de γ. L'adjonction est autorisée si la catégorie du nœud x est identique à la catégorie du nœud racine de γ. Intuitivement l'opération d'adjonction permet d'insérer l'arbre γ dans l'arbre β.

Dérivation

Propriétés formelles

Langage d'une grammaire d'arbres adjoints Un arbre dérivé complet est un arbre dérivé dont la racine est l'axiome de la grammaire. Le langage généré par une grammaire d'arbres adjoints est l'ensemble des séquences qui forment le feuillage de tout arbre dérivé complet dérivable par la grammaire.

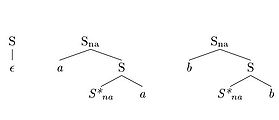
Classe de langages d'une grammaire d'arbres adjoints Une grammaire d'arbres adjoints engendre l'ensemble des langages hors-contexte ainsi que des langages contextuels comme le langage 2-copie ($ww|w\in \{a,b\}^{*}$) ou le langage $a^{n}b^{n}c^{n}d^{n}$. Par contre aucune grammaire d'arbres adjoints n'engendre le langage 3-copie ($www|w\in \{a,b\}^{*}$) ou le langage $a^{n}b^{n}c^{n}d^{n}e^{n}$. Autrement dit, les grammaires d'arbres adjoints engendrent des langages qui forment un sous-ensemble des langages contextuels. Ceux-ci sont appelés langages légèrement sensibles au contexte.

• 
  Langage $a^{n}b^{n}c^{n}d^{n}$
• 
  Langage 2-copie : ${ww|w\in \{a,b\}^{*}}$

Extension de la hiérarchie de Chomsky

• Langages réguliers
• Langages hors-contexte
• Langages légèrement sensibles au contexte
• Langages contextuels
• Langages récursivement énumérables

Grammaire d'arbres adjoints lexicalisée

Une grammaire d'arbres adjoints lexicalisée est une grammaire d'arbres adjoints dans laquelle tout arbre élémentaire est muni d'au moins un symbole terminal appelé nœud ancre. Une grammaire d'arbres adjoints lexicalisée est un formalisme fortement lexicalisé au même titre que les grammaires catégorielles. Un formalisme fortement lexicalisé est un formalisme dans lequel tout objet grammatical comporte au moins un élément terminal. La propriété fondamentale sous-jacente à l'intérêt porté à la grammaire d'arbres adjoints lexicalisée en linguistique formelle est que les grammaires d'arbres adjoints lexicalisent fortement les grammaires de réécriture hors-contexte.

Lexicalisation Un formalisme F' lexicalise un formalisme F si pour toute grammaire finiment ambigüe G définie dans F on peut trouver une grammaire lexicalisée G' formulée en F' telle que L(G) = L(G'). Une grammaire de réécriture hors contexte se lexicalise par une grammaire de réécriture hors contexte par mise en forme normale de Greibach. Une grammaire en forme normale de Greibach est une grammaire dont les productions sont de la forme A → b B où A ∈ N, b ∈ T, B ∈ (N ∪ T)*. Il existe un algorithme dû à Hopcroft et Ullmann (ref ?) qui permet d'opérer la conversion. La mise en forme normale de Greibach est un exemple de lexicalisation faible d'une grammaire. La mise en forme normale de Greibach d'une grammaire G par l'algorithme de Hopcroft produit une grammaire G' telle que L(G) = L(G'). Cependant, cette transformation ne garantit pas que l'ensemble des arbres de dérivation de G et de G' sont identiques. La lexicalisation forte d'une grammaire impose la contrainte supplémentaire que les arbres engendrés par la grammaire sont identiques.

Depuis Chomsky (1956), on sait que la dérivation d'une grammaire de réécriture hors-contexte s'interprète par un arbre appelé arbre de dérivation. En prolongeant cette interprétation, la génération d'une phrase par une grammaires hors contexte s'interprète comme une composition d'arbres élémentaires de profondeur 1 (les règles de grammaire) en utilisant la substitution (définie ci-dessus).

Grammaire de substitution d'arbres Il est possible de généraliser les grammaires hors contexte en autorisant la composition d'arbres de profondeur quelconques par substitution. Cette généralisation mène à la définition de grammaires de substitution d'arbres. Une grammaire de substitution d'arbres est un 4-uple :

• N un ensemble de symboles non terminaux
• T un ensemble de symboles terminaux (avec N et T disjoints)
• S un axiome (S est un élément de N)
• A un ensemble d'arbres initiaux tels que les nœuds non feuilles sont étiquetés par des symboles non terminaux, et tel que les nœuds feuilles sont étiquetés par un terminal ou un non terminal. Dans ce dernier cas, le nœud est un nœud de substitution.

Une grammaire de substitution d'arbres est munie d'une opération de composition, la substitution (définie ci-dessus).

Non lexicalisation d'une grammaire hors-contexte par une grammaire de substitution d'arbres Une grammaire de substitution d'arbres ne permet pas de lexicaliser toute grammaire hors contexte finiment ambigüe.

La preuve est par contradiction : soit la grammaire hors contexte G telle que S → S S, S → a. La grammaire de substitution d'arbres T_G qui lexicalise G comporte un ensemble d'arbres initiaux tel que dans chacun de ces arbres, le chemin entre la racine et le terminal a est de longueur constante n. Parmi ces arbres il existe un arbre pour lequel la longueur du chemin n est maximale. Ce chemin est noté n-max. En conséquence, il n'existe pas d'arbre dérivé engendré par la grammaire T_G tel que tous les chemins de la racine à toute feuille ont une longueur supérieure à n-max. Or de tels arbres sont dérivables par G ce qui mène à la contradiction.

On a comme conséquence immédiate qu'une grammaire hors-contexte ne permet pas de lexicaliser fortement une grammaire hors-contexte.

Opération d'adjonction Pour engendrer des arbres dérivés dont l'ensemble des branches sont de longueur potentiellement quelconques, il est nécessaire de disposer d'une opération qui permet l'insertion d'un arbre dans un autre. Cette opération est l'adjonction.

Intérêt en linguistique formelle

La grammaire d'arbres adjoints a connu un certain succès en linguistique formelle et informatique pour les raisons suivantes. Le système formel qui définit des langages légèrement sensibles au contexte permet l'analyse de dépendances croisées, phénomène qui ne peut se représenter avec une grammaire hors contexte et facilite l'expression directe de dépendances dans des unités grammaticales (les arbres) à domaine de localité étendu :

• Lexicalisation et représentation locale des dépendances syntaxiques (domaine de localité étendu) Une grammaire d'arbres adjoints lexicalisée permet de représenter des règles de grammaire (par des arbres élémentaires) lexicalisées de profondeur quelconque. Formellement, il est donc possible de représenter localement au sein d'un même arbre élémentaire un prédicat et les points de composition avec les arbres élémentaires de ses dépendants.
• Dépendances à longue distance et contraintes d'îlots (factorisation de la récursivité hors du domaine de localité) La représentation locale de la dépendance est non seulement possible pour les cas triviaux mais également dans les cas de dépendances à longue distance :

Quels cadeaux[i] Jean souhaite-t-il offrir à Marie [i] ?

Quels cadeaux[i] pensez-vous que Jean souhaite offrir à Marie [i] ?

Ces exemples illustrent le fait que les langues naturelles permettent théoriquement de réaliser un dépendant à une distance potentiellement non bornée du prédicat. Il est ainsi possible d'ajouter récursivement à ces exemples un nombre quelconque (non borné) d'enchâssements entre le prédicat offrir et son dépendant cadeaux. Or dans de tels cas, la grammaire d'arbres adjoints permet en effet de représenter localement ces dépendances en utilisant l'adjonction. L'adjonction est ainsi utilisée pour représenter les structures récursives de la grammaire, ainsi la phrase complexe sera analysée avec une structure du type :

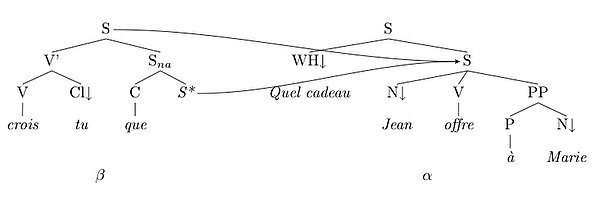
où l'arbre auxiliaire (β) est la structure récursive insérée dans l'arbre initial (α). L'arbre initial comporte localement au sein de la même structure grammaticale un prédicat et un site de composition pour chacun de ses arguments. Formellement, l'adjonction est utilisée ici car la distance entre la racine de α et son ancre lexicale ne peut être raisonnablement bornée.

• Dépendances croisées. S. Shieber a donné des exemples de productions langagières qui ne s'analysent pas avec une grammaire hors-contexte. On en conclut que les grammaires hors-contexte ne constituent pas un mécanisme suffisamment général pour analyser le langage naturel dans son ensemble. Les exemples de Shieber traitent du Suisse Allemand. On trouve la même classe d'exemples dans une langue plus répandue, le néerlandais, où les verbes qui sous-catégorisent une infinitive (modaux, perception) se comportent comme illustré ici :

Jan denkt dat An[a] Bea[b] wil[a] kussen[b]

Jean pense que Anne Béatrice va embrasser

Jean pense que Anne va embrasser Béatrice

Or cette catégorie d'exemples se réduit à une variante du langage 2-copie (illustré ci-dessus) et le langage copie est un langage qui appartient à la classe de langage de la grammaire d'arbres adjoints mais pas à la classe des langages hors-contexte (le langage copie est un langage contextuel). La grammaire d'arbres adjoints est connue pour engendrer la plus petite classe de langage formelle connue qui permet de capturer formellement l'ensemble des productions du langage humain. Cette classe forme la classe des langages légèrement sensibles au contexte.

Extensions

On présente ici les extensions les plus courantes aux grammaires d'arbres adjoints, Multi-Component TAG, TAG stochastique, TAG synchrone et TAG avec structures de traits.

TAG ensembliste (MC-TAG)

Multi-Component TAG (MC-TAG) ou TAG ensembliste est une extension de TAG décrite en détail par D. Weir en 1988. Il s'agit d'un formalisme qui engendre exactement la même classe de langages que la classe des langages d'un système linéaire de réécriture non contextuel (LCFRS).

MC-TAG est une extension qui offre des facilités d'expression supplémentaires à TAG et qui génère une classe de langage incluant la classe de langage de TAG. Dans une TAG, l'opération d'adjonction permet en effet d'exprimer que la distance entre la racine et l'ancre d'un arbre élémentaire est potentiellement non bornée en insérant des arbres auxiliaires de catégorie et de nœud pied identiques dans un arbre. Cependant il existe des cas où la distance entre l'ancre et la racine de cet arbre est bornée mais difficile à prédéfinir dans un arbre élémentaire. Il s'agit en quelque sorte de cas de "semi-récursivité".

Définition Une MC-TAG est une TAG augmentée de l'élément suivant :

• Un ensemble S ⊆ Pow(I ∪ A), qui est un ensemble fait de sous-ensembles des arbres élémentaires

On peut contraindre la composition de différentes manières dans une MC-TAG, ce qui définit trois sous-types de formalismes :

• Les arbres appartenant à un même ensemble doivent être adjoints ou substitués sur un arbre unique. Dans ce cas, il s'agit d'une TAG ensembliste locale à un arbre (Tree Local MC-TAG). Une TAG ensembliste locale à un arbre est fortement équivalente à une TAG standard avec contraintes de composition et apporte donc peu de nouveauté.
• Les arbres appartenant à un même ensemble doivent être adjoints ou substitués dans un ensemble unique. Dans ce cas, il s'agit d'une TAG ensembliste locale à un ensemble (Set Local MC-TAG)
• Les arbres appartenant à un même ensemble sont adjoints ou substitués à des arbres quelconques. Dans ce cas, il s'agit d'une TAG ensembliste non locale (Non Local MC-TAG).

TAG stochastique

Les grammaires d'arbres adjoints stochastiques (ou probabilistes) définissent un modèle de langage. Comme pour les grammaires de réécritures hors contexte probabilistes, la motivation première de cette extension est la possibilité pratique d'ordonner différentes analyses concurrentes pour une phrase ambigüe.

Notation Soit α un arbre élémentaire, dénotons par s(α) l'ensemble des nœuds de substitution de cet arbre. Dénotons par a(α) l'ensemble des nœuds η dans α susceptibles de recevoir une adjonction (par définition de TAG on a également que s(α)∩a(α) = ∅).

• L'événement noté S(α,α',η) dénote l'événement que l'arbre α' est substitué sur le nœud η de α.
• L'événement noté A(α,α',η) dénote l'événement que l'arbre α' est adjoint sur le nœud η de α.
• L'ensemble fondamental Ω est par conséquent l'ensemble de tout événement adjonction ou de substitution.

Définition Une grammaire TAG stochastique est une grammaire TAG augmentée des éléments suivants :

• π(I), la distribution initiale est une fonction des arbres initiaux (I) dans l'intervalle réel [0,1]
• P_S, est une fonction des événements de substitution S dans l'intervalle réel [0,1]
• P_A, est une fonction des événements d'adjonction A dans l'intervalle réel [0,1]

respectant les contraintes suivantes :

• $\sum _{\alpha \in I}\pi (\alpha )=1$
• $\forall _{\alpha \in I\cup A}\forall _{\eta \in s(\alpha )}\sum _{\alpha '\in I}P_{S}(S(\alpha ,\alpha ',\eta ))=1$
• $\forall _{\alpha \in I\cup A}\forall _{\eta \in a(\alpha )}\sum _{\alpha '\in A\cup NA}P_{A}(A(\alpha ,\alpha ',\eta ))=1$

où NA représente la non adjonction en η.

Modèle de langage En dénotant α₀ l'arbre initial avec lequel la dérivation commence et chaque opération de dérivation op(α1,α2,η) (avec op ∈ {S,A}), la probabilité d'une dérivation δ = <α₀,op₁(...) , etc. , op_n(...)> est la suivante :

$P(\delta )=\pi (\alpha _{0})\prod _{1\leq i\leq n}P_{op_{i}}(op_{i}(...))$

TAG stochastique est un modèle de langage. La probabilité d'une phrase w₀...w_n est la probabilité de l'ensemble des arbres dérivés dont cette phrase est le feuillage :

$P(w_{0}\ldots w_{n})=\sum _{\delta :yield(\delta )=w_{0}\ldots w_{n}}P(\delta )$

Constatons que la définition du modèle probabiliste TAG est une contrepartie directe du modèle utilisé pour les grammaires non contextuelles. Dans une grammaire hors contexte probabiliste, une dérivation δ = <Axiome,r₁, etc.,r_n> est associée à la probabilité suivante :

$P(\delta )=P(Axiome)\prod _{1\leq i\leq n}P(r_{i})$

où r_i dénote une opération de réécriture. Dans le cas de la grammaire non contextuelle P(Axiome) = 1 et est généralement omise dans la définition.

Estimation par maximum de vraisemblance Dans le cas supervisé (cas où on dispose d'un échantillon annoté, comme une banque d'arbres), l'estimation de paramètres pour une grammaire TAG stochastique par maximum de vraisemblance est réalisée comme suit :

• $\pi (\alpha )={\frac {C(\alpha )}{\sum _{\alpha '\in I}C(\alpha ')}}$
• $P_{S}(\alpha ,\alpha ',\eta )={\frac {C(\alpha ,\alpha ',\eta )}{\sum _{\alpha '\in I}C(\alpha ,\alpha ',\eta )}}$
• $P_{A}(\alpha ,\alpha ',\eta )={\frac {C(\alpha ,\alpha ',\eta )}{\sum _{\alpha '\in A\cup NA}C(\alpha ,\alpha ',\eta )}}$

où C(...) dénote une fonction de comptage dans l'échantillon.

Intérêt de TAG stochastique L'utilisation de grammaires de réécritures non contextuelles pour l'analyse du langage naturel est souvent critiquée pour les raisons suivantes :

• Les Hypothèses d'indépendance conditionnelles du modèle sont trop fortes
• Ces modèles ne tiennent pas compte des propriétés lexicales

Par ses propriétés formelles, TAG stochastique répond à ces deux problèmes. Le domaine de localité étendu de TAG permet d'apporter une réponse à la première critique. La propriété de lexicalisation forte des grammaires de réécriture non contextuelles de TAG permet, dans le cas d'une grammaire lexicalisée, d'estimer des probabilités qui capturent des dépendances lexicales non seulement entre la tête et les arguments mais aussi entre la tête et les modifieurs.

Cependant, en pratique, il est indispensable de traiter un problème de dispersion de donnée considérablement accru par l'usage d'un formalisme de ce type. Les travaux récents menés sur Spinal TAG traitent astucieusement cette question par utilisation d'arbres élémentaires arguments, adjoints dynamiquement au spine des arbres prédicatifs.

Annexes

Bibliographie

• Aravind K. Joshi et Yves Schabes, « Tree-adjoining grammars », dans G. Rosenberg et A. Salomaa (éditeurs), Handbook of Formal Languages, vol. 3 : Beyond Words, Springer, 1997, p. 69-123.
• Aravind K. Joshi, Leon S. Levy et Masako Takahashi, « Tree Adjunct Grammars », Journal of Computer and Systems Sciences, vol. 10, n^o 1,‎ 1975, p. 55-75 (DOI 10.1016/S0022-0000(75)80019-5).
• Anne Abeillé et Owen Rambow (éditeurs), Tree Adjoining Grammars: Formalisms, Linguistic Analysis and Processing, Stanford (CA), Center for the Study of Language and Information (CSLI), 2000 (ISBN 1575862514).
• David Weir, Characterizing mildly context sensitive languages, thèse de doctorat, université de Pennsylvanie, 1988.
• K. Vijay-Shanker, A study of tree adjoining grammars, thèse de doctorat, université de Pennsylvanie, 1987.
• Stuart M. Shieber, « Evidence against the context-freeness of natural language », Linguistics and Philosophy, vol. 8,‎ 1985, p. 333-343.
• Anthony Kroch et Aravind K. Joshi, The Linguistic Relevance of Tree Adjoining Grammar, University of Pennsylvania, Department of Computer and Information Science, 1985, Technical Report n^o MS-CIS-85-16.
• Aravind K. Joshi, « How much context-sensitivity is necessary for characterizing structural descriptions », dans D. Dowty, L. Karttunen et A. Zwicky (éditeurs), Natural Language Processing: Theoretical, Computational, and Psychological Perspectives, New York, NY, Cambridge University Press, 1985, p. 206–250.

Liens externes

• Le projet XTAG, historiquement la première implantation d'une taille conséquente d'une TAG.
• Un tutoriel sur les TAG
• Un autre tutoriel se concentrant sur les points communs et différences entre les TAG et le formalisme LFG Lexical Functional Grammar. Une partie est consacrée à l'extration de grammaires à partir de Corpus arborés Treebank
• Doc de SemConst Une étude sur les problèmes d'interfaces syntaxe sémantiques dans le paradigme des Grammaires d'Arbres adjoints
• The TuLiPa project "Tübingen Linguistic Parsing Architecture" (TuLiPA) est un environnement d'analyse syntaxique (ie parsing) et sémantique multi-formalismes, conçu principalement pour l'analyse des MC-TAG Multi-Component Tree Adjoining Grammars avec Tree Tuples
• The Metagrammar Toolkit propose plusieurs outils pour concevoir et compiler des métagrammaires MetaGrammars vers des TAGs. Inclut aussi une Grammaire d'Arbres Adjoints à large couverture pour le français.
• LLP2 Un analyseur LTAG Lexicalized Tree Adjoining Grammar qui propose un environnement graphique facile d'accès