Diagramme de Hasse
En mathématiques, le diagramme de Hasse, du nom du mathématicien allemand Helmut Hasse, est une représentation visuelle d'un ordre fini. Similaire à la représentation habituelle d’un graphe sur papier, il en facilite la compréhension.
Dans un diagramme de Hasse :
- Les éléments ordonnés sont représentés par des points.
- La relation entre deux éléments est représentée par un segment entre deux points.
- Si un élément x est ≤ à un autre élément y, alors le point représentant x est placé plus bas que celui pour y. Ainsi, les segments n'ont pas besoin d'être fléchés pour avoir leur orientation décrite.
- Afin d'éviter de surcharger le schéma, les relations d’ordre possibles ne sont pas toutes représentées. Elles sont limitées à la réduction réflexive transitive :
- Lorsque x < y, s'il existe z tel que x < z < y, alors aucun segment ne doit lier x à y.
- Les boucles d’un élément vers lui-même ne sont pas représentées.
- On veille autant que possible à ne pas croiser les segments.
À noter qu'en cas d’ordre infini, on peut quand même utiliser le diagramme de Hasse et représenter une restriction finie de l’ordre.
Exemples de diagramme de Hasse[modifier | modifier le code]
- Un ensemble ordonné de onze éléments dont les trois maximums sont les trois majorants et l'élément minimum est à la fois l'unique minorant et la borne inférieure de l'ensemble.

- Pour l'ensemble des diviseurs de 60, A = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}, ordonnés par la relation de divisibilité, on obtient le diagramme de Hasse suivant :

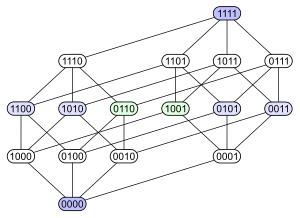
- L’ensemble S = A ∪ B ∪ C ∪ D, où A, B, C et D sont des quadruplets de booléens représentant les combinaisons possibles des parties de S, tels que,
- A = { 1000={a}, 1100={a, b}, 1010={a, c}, 1001={a, d}, 1110={a, b, c}, 1101={a, b, d}, 1011={a, c, d}, 1111={a, b, c, d} }
B = { 0100={b}, 1100={a, b}, 0110={b, c}, 0101={b, d}, 1110={a, b, c}, 1101={a, b, d}, 0111={b, c, d}, 1111={a, b, c, d} }
C = { 0010={c}, 1010={a, c}, 0110={b, c}, 0011={c, d}, 1110={a, b, c}, 1011={a, c, d}, 0111={b, c, d}, 1111={a, b, c, d} }
D = { 0001={d}, 1001={a, d}, 0101={b, d}, 0011={c, d}, 1101={a, b, d}, 1011={a, c, d}, 0111={b, c, d}, 1111={a, b, c, d} } - S = { 0000={}, 1000={a}, 0100={b}, 0010={c}, 0001={d}, 1100={a, b}, 1010={a, c}, 1001={a, d}, 0110={b, c}, 0101={b, d}, 0011={c, d}, 1110={a, b, c}, 1101={a, b, d}, 1011={a, c, d}, 0111={b, c, d}, 1111={a, b, c, d} }
Ainsi, à partir des seize quadruplets ordonnés par la relation d'inclusion, on obtient le diagramme de Hasse suivant :
 |
 |
 |

|
Ces quatre figures représentent toutes le même diagramme de Hasse mais sous des aspects distincts afin de mettre en évidence différentes propriétés :
- Le premier diagramme illustre le fait que l'ensemble des parties (de S) est un ensemble partiellement ordonné gradué : le rang de chaque élément (partie de S) correspond à sa hauteur dans le diagramme ;
- Le deuxième diagramme respecte également cette correspondance entre rang et hauteur, mais y ajoute par étirement de certaines arêtes une mise en valeur du tesseract comme union de deux cubes (en interprétant les quadruplets de booléens comme des coordonnées en dimension 4, chacun correspondant alors à un sommet de l'hypercube) ;
- Le troisième diagramme met l'accent sur la symétrie interne de la structure ;
- Le quatrième diagramme présente des sommets disposés de manière analogue aux coefficients d'une matrice carrée d'ordre 4.
