Code de Gray

Le code de Gray, également appelé code Gray ou code binaire réfléchi, est un type de codage binaire permettant de ne modifier qu'un seul bit à la fois quand un nombre est augmenté d'une unité. Cette propriété est importante pour plusieurs applications.
Le nom du code vient de l'ingénieur américain Frank Gray qui publia un brevet sur ce code en 1953, mais le code lui-même est plus ancien.
Principe et exemple[modifier | modifier le code]
Le code de Gray est un codage binaire, c'est-à-dire une fonction qui associe à chaque nombre une représentation binaire. Cette méthode est différente du codage binaire naturel. Le tableau suivant montre partiellement le codage sur 4 bits (seules les 8 premières valeurs sont présentées, les huit suivantes avec le premier bit à 1 n'y sont pas).
| Codage décimal | Codage binaire naturel | Codage Gray ou binaire réfléchi |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
La différence principale entre les deux est le fait que le codage de Gray de deux nombres consécutifs ne diffère que d'une position. Par exemple 5 est codé par 0111, et 6 est codé par 0101 : ici seul le deuxième bit change.
Construction de la table par symétrie[modifier | modifier le code]

Le nom de code binaire réfléchi, comme autre nom du code de Gray, vient d'une méthode de construction basée sur la réflexion de blocs de codes déjà construits :
- on choisit un code de départ : zéro est codé 0 et un est codé 1,
- puis, à chaque fois qu'on a besoin d'un bit supplémentaire, on symétrise la liste des codes déjà obtenus (comme une réflexion dans un miroir),
- enfin, on rajoute un 0 puis un 1 au début (à gauche) de chacun des codes. On a ainsi doublé le nombre de codes formés.
Exemple :
0 0 0 .0 0 00 0 .00 0 000
1 1 1 .1 1 01 1 .01 1 001
miroir→------ 2 .11 2 011
2 .1 2 11 3 .10 3 010
3 .0 3 10 -------
4 .10 4 110
5 .11 5 111
6 .01 6 101
7 .00 7 100
Méthodes d'incrémentation[modifier | modifier le code]
Il existe plusieurs méthodes pour incrémenter un nombre écrit selon le code de Gray (c'est-à-dire lui ajouter 1).
Inverser pour obtenir un nouveau nombre[modifier | modifier le code]
Pour passer d'une ligne à la suivante, on inverse le bit le plus à droite possible conduisant à un nombre nouveau. Cette méthode présente l'inconvénient de devoir connaître tous les codes de Gray qui précèdent.
Selon la parité[modifier | modifier le code]
Une autre méthode de calcul permettant de passer d'un nombre de Gray au suivant, et qui présente l'avantage de ne pas nécessiter de connaître l'ensemble des nombres précédents est la suivante :
- si le nombre de 1 est pair, il faut inverser le dernier chiffre.
- si le nombre de 1 est impair, il faut inverser le chiffre situé à gauche du 1 le plus à droite.
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
Calcul de moitié et double[modifier | modifier le code]
Une méthode de calcul de la moitié d'un nombre pair consiste à éliminer le dernier chiffre et donc décaler les autres chiffres d'une position à droite.
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
Une méthode de calcul du double d'un nombre consiste à insérer un chiffre supplémentaire à droite et donc décaler les autres chiffres d'une position à gauche.
- si le nombre de chiffres 1 est pair, le nombre est pair, il faut insérer un zéro à droite
- si le nombre de chiffres 1 est impair, le nombre est impair, il faut insérer le chiffre 1 à droite
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
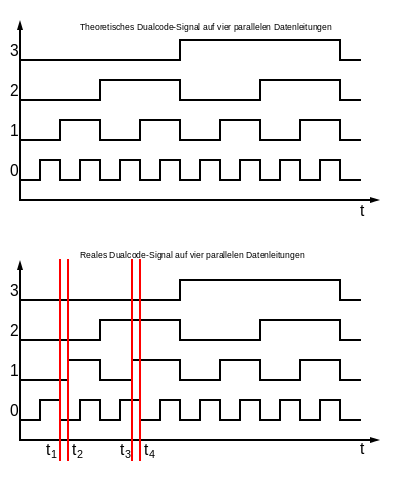
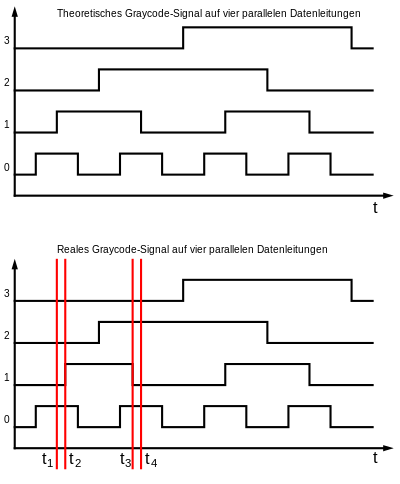
Intérêt: Éviter des états transitoires[modifier | modifier le code]
Le fait de modifier plusieurs bits lors d'une simple incrémentation peut mener, selon le circuit logique, à un état transitoire indésirable dû au fait que le chemin logique de chaque bit dispose d'un délai différent. Ainsi, lors du passage de la valeur "01" à la valeur "10" en binaire naturel, il est possible d'observer un état transitoire "00" si le bit de droite commute en premier ou "11" dans le cas contraire. Si le circuit dépendant de cette donnée n'est pas synchrone, l'état transitoire peut perturber les opérations en faisant croire au système qu'il est passé par un état normalement non atteint à ce stade. Cela apparait pour les capteurs de positions, par exemple sur des règles optiques. Ce code permet de contourner cet aléa en forçant la commutation d'un seul bit à la fois, évitant ainsi les états transitoires.
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Applications[modifier | modifier le code]
Roue codeuse[modifier | modifier le code]

Le code de gray trouve une application pratique dans la roue codeuse. Dans l'illustration, on trouve huit états et huit transitions sans qu'il n'y ait ni maximum, ni minimum, du fait des symétries. Chaque huitième de tour n'occasionne qu'une unique transition. Ceci permet donc bien d'encoder un angle.
L'illustration montre la forme de la roue, la table montre les transitions entre états, le graphe montre la position les transitions sur la roue. Le code est implémenté en noir et blanc, pour explication, les transitions sont explicitées en rouge, vert et bleu.
Ces explications prennent comme références les directions d'une girouette (E=est, N=nord, O=ouest, S=sud).
| Transition | i | .... | e | .... | m | .... | e | .... | i | .... | e | .... | m | .... | e | .... | i | .... | e | .... | m | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cercle extérieur | Est | Nord | Ouest | Sud | Est | Nord | ||||||||||||||||||
| Cercle médian | Est | N | Ouest | S | Est | N | ||||||||||||||||||
| Cercle intérieur | E | Nord | O | Sud | E | Nord | ||||||||||||||||||
| Transition | i | .... | e | .... | m | .... | e | .... | i | .... | e | .... | m | .... | e | .... | i | .... | e | .... | m | |||
Souris[modifier | modifier le code]
Le décodage des signaux lumineux d'un axe de souris mécanique est un décodage de code de Gray à 2 bits (décodage différentiel dans ce cas, car ce que l'on veut obtenir n'est pas la valeur décodée mais les transitions ±1 mod 4 de la valeur décodée).
Tables de Karnaugh[modifier | modifier le code]
Le code Gray sert également dans les tables de Karnaugh utilisées lors de la conception de circuits logiques.
Code Baudot[modifier | modifier le code]
Le principe du code de Gray se retrouve dans le code Baudot, dans lequel les voyelles et les consonnes sont classées dans leur ordre alphabétique, et un seul bit change entre deux lettres successives.
Otto Schäffler aurait également eu un télégraphe similaire.
Let ·Fig. · V · IV· · I · II·III· ----+-----+---+---+---+---+---+---+ A · 1 · · · · ● · · · É / · 1/ · · · · ● · ● · · E · 2 · · · · · ● · · I · 3/ · · · · · ● · ● · O · 5 · · · · ● · ● · ● · U · 4 · · · · ● · · ● · Y · 3 · · · · · · ● · B · 8 · · ● · · · · ● · C · 9 · · ● · · ● · · ● · D · 0 · · ● · · ● · ● · ● · F · 5/ · · ● · · · ● · ● · G · 7 · · ● · · · ● · · H · ¹ · · ● · · ● · ● · · J · 6 · · ● · · ● · · · Fig. Bl. · · ● · · · · · * · * · ● · ● · · · · K · ( · ● · ● · · ● · · L · = · ● · ● · · ● · ● · M · ) · ● · ● · · · ● · N · £ · ● · ● · · · ● · ● P · + · ● · ● · · ● · ● · ● Q · / · ● · ● · · ● · · ● R · – · ● · ● · · · · ● S · 7/ · ● · · · · · ● T · ² · ● · · · ● · · ● V · ¹ · ● · · · ● · ● · ● W · ? · ● · · · · ● · ● X · 9/ · ● · · · · ● · Z · : · ● · · · ● · ● · – · . · ● · · · ● · · Let. Bl. · ● · · · · · ·
Transcodage binaire[modifier | modifier le code]
Transcodage binaire / Gray[modifier | modifier le code]
En notant un entier écrit en binaire (où est le bit de poids fort), et de même en notant le code de Gray correspondant, il est possible de montrer (par exemple en utilisant les tables de Karnaugh), que (où désigne la fonction OU exclusif) ; autrement dit, pour obtenir , il suffit d'effectuer un OU exclusif entre et ce même nombre décalé d'un bit vers la droite (c'est-à-dire, en binaire, divisé par 2), ce qu'exprime la fonction suivante écrite en langage C :
Algorithme de codage d'un nombre b en code de Gray :
g = b ^ (b >> 1)
Par exemple, le nombre décimal 7 s'écrit 0111 en base 2. Son code de Gray s'obtient comme suit :
0111 ^ 0011 ------ 0100
7 est représenté par 0100 en code de Gray.
Algorithme de décodage rapide pour des mots de 64 bits (pour des mots de 32 bits, remplacer 32 par 16) :
long grayInverse(long n) {
long ish, ans, idiv;
ish = 1;
ans = n;
while(1) {
idiv = ans >> ish;
ans ^= idiv;
if (idiv <= 1 || ish == 32)
return ans;
ish <<= 1; // double le nb de shifts la prochaine fois
}
}
Transcodage Gray / binaire[modifier | modifier le code]
En notant un entier écrit en binaire (où est le bit de poids fort), et de même en notant le code de Gray correspondant, selon ce qui précède, on détermine facilement le nombre binaire d'un code de Gray donné : (où désigne la fonction OU exclusif). On a donc :
etc.
Donc pour obtenir le code binaire d'un code de Gray donné, on passe de gauche (poids fort) à droite (poids faible). Le bit de poids fort est le même en binaire que dans le code de Gray . Le bit binaire suivant reste le même si le bit de Gray suivant vaut zéro et change si le bit de Gray suivant vaut 1. On répète cela pour tous les bits, jusqu'au bit de poids le plus faible.
Historique[modifier | modifier le code]
L'ingénieur américain Frank Gray déposa un brevet sur ce code en 1947[1], mais le code est plus ancien ; il a notamment été utilisé dans le code Baudot.
Luc-Agathon-Louis Gros, qui fut clerc de notaire puis conseiller à la Cour d'appel de Lyon, publia en 1872 un opuscule, Théorie du baguenodier par un clerc de notaire lyonnais, où ce code était présenté pour la première fois en lien avec un casse-tête, le jeu du baguenaudier[2].
Cette séquence a été notamment vulgarisée dans le jeu du baguenaudier[3] (jeu qui nous a été transmis par Jérôme Cardan et qui a été résolu par John Wallis).
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Références[modifier | modifier le code]
- (en) Frank Gray pour Bell Labs, Brevet U.S. 2,632,058 : Pulse code communication, déposé le 13 novembre 1947, publié le 17 mars 1953, sur Google Patents.
- Luc-Agathon-Louis Gros, Théorie du baguenodier par un clerc de notaire lyonnais, Lyon, Aimé Vingtrinier, (lire en ligne).
- Édouard Lucas, Récréations mathématiques, vol. 1, Paris, Gauthier-Villars, , « Septième récréation : Le jeu du baguenaudier », p. 161–186 : dans le « Tableau des deux marches du Baguenaudier », p. 185–186, on trouve les valeurs du code de Gray dans la colonne Baguenaudes.