Éléments d'Argyris

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

Cet article ne cite pas suffisamment ses sources (octobre 2018).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

Les fonctions d'Argyris (ou éléments d'Argyris) sont un outil en méthodes des éléments finis. Elles sont utilisées pour décrire un polynôme dans un triangle d’un maillage en employant seulement des données connues sur le bord du triangle. Utilisées en modélisation numérique, ces fonctions furent introduites dans les années 1950 ; mais d'autres styles de fonctions sont également employés en pratique en fonction des problèmes à résoudre.

Introduction[modifier | modifier le code]

Contexte[modifier | modifier le code]

John Hadji Argyris (1913-2004)^[1]^,^[2] est l’un des précurseurs dans le domaine des méthodes des éléments finis, utilisée lors de résolution numérique d’équations différentielles issues de la physique, mécanique… comme la théorie des plaques. Ses concepts sont apparus en premier lors de la Seconde Guerre mondiale, ce qui rendait ses premiers résultats top secret.^{[réf. nécessaire]}

Le principe des fonctions d'Argyris consiste à exprimer un polynôme avec pour seules informations des données relatives au maillage du domaine. D'autres fonctions sont utilisées en méthodes des éléments finis (Lagrange, Raviart-Thomas, Nédélec, Gauss-Lobatto, Hermite, Morley, Bell…) ayant chacune leurs avantages ainsi que leurs inconvénients (tout dépend du problème que l'on veut résoudre).

Les éléments d'Argyris désignent couramment la construction sur un problème 2D ; pour les versions analogues 1D ou 3D, on parle plutôt d'éléments de type Argyris.

Cadre d’étude[modifier | modifier le code]

On se place dans le plan. Les variables sont appelées x et y. Soit ${\mathcal {T}}$ un triangle quelconque, non aplati.

Les fonctions d'Argyris liées à ${\mathcal {T}}$ sont des fonctions de base de l'espace vectoriel $\mathbb {P} _{5}({\mathcal {T}})$ qui représente l'ensemble des polynômes à deux variables x et y ( $(x,y)\in {\mathcal {T}}$ ) de degré au plus 5.

Approche formelle[modifier | modifier le code]

Un élément $M\in \mathbb {P} _{5}({\mathcal {T}})$ s'écrit donc de manière unique sous la forme

M(x,y)=a_{0}+a_{1}x+b_{1}y+a_{2}x^{2}+b_{2}xy+c_{2}y^{2}+a_{3}x^{3}+b_{3}x^{2}y+c_{3}xy^{2}+d_{3}y^{3}+a_{4}x^{4}+b_{4}x^{3}y+c_{4}x^{2}y^{2}+d_{4}xy^{3}+e_{4}y^{4}+a_{5}x^{5}+b_{5}x^{4}y+c_{5}x^{3}y^{2}+d_{5}x^{2}y^{3}+e_{5}xy^{4}+f_{5}y^{5}

.

Ainsi, la seule donnée des 21 coefficients du polynôme suffit à écrire tout élément de $\mathbb {P} _{5}({\mathcal {T}})$ .

Il est alors nécessaire d'avoir 21 relations (conditions) indépendantes afin de pouvoir déterminer de façon unique ces coefficients.

Une base possible serait de travailler sur la base canonique $\{1,x,y,x^{2},xy,y^{2},x^{3},x^{2},y^{2},y^{3},x^{4},x^{3}y,x^{2}y^{2},xy^{3},y^{4},x^{5},x^{4}y,x^{3}y^{2},x^{2}y^{3},xy^{4},y^{5}\}$ , mais dans la pratique, il est extrêmement difficile de pouvoir trouver les 21 coefficients avec cette base. Argyris propose donc une autre base, liées à des conditions données :

sur la valeur de la fonction M en chaque sommet (3 relations) ;
sur la valeur des dérivées premières de la fonction M en chaque sommet (6 relations) ;
sur la valeur des dérivées secondes de la fonction M en chaque sommet (9 relations) ;
sur la valeur "liée à la normale" pour chaque arête (3 relations).

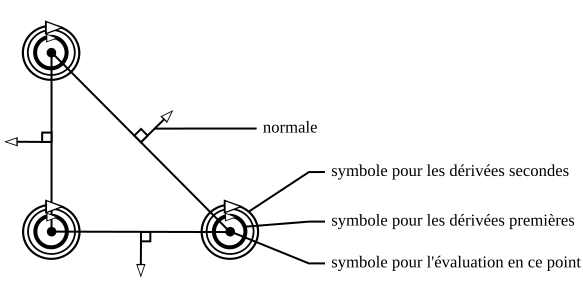
Avec ces données, il est possible de calculer toutes les fonctions d'Argyris pour n'importe quel triangle : il suffit pour cela de résoudre un système linéaire $A u = b$ où :

$A$ est une matrice 21×21;
$u$ est un vecteur de taille 21 composé des 21 coefficients;
$b$ est un vecteur de taille 21 dont toutes les composantes sont nulles sauf une qui correspond à la condition adéquate.

Régularité des solutions[modifier | modifier le code]

Par les conditions imposées aux bords des mailles triangulaires, les solutions calculées par éléments d'Argyris sont régulières (au moins C²). Plus précisément, l'élément fini d'Argyris est celui H²-conforme de plus bas degré. Ils sont donc adaptées aux problèmes d'ordre élevée (bilaplacien) mais reste coûteux.

Logiciels gérant les éléments d’Argyris[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

getfem++
matlab

Bibliographie[modifier | modifier le code]

V. Girault, P.-A. Raviart. Finite Element Methods for Navier-Stokes Equations. Theory and algorithms. Springer Series in Computational Mathematics, 5. Springer-Verlag, Berlin, 1986.
S. Nicaise, K.Witowski and B. I. Wohlmuth. An a posteriori error estimator for the Lamé equation based on equilibrated fluxes. IMA Journal of Numerical Analysis, 28, n^o 2, p. 331-353, 2008.
Librairie de getfem++
V. Domínguez, F.J. Sayas. Algorithm 884: A simple MATLAB implementation of the Argyris element. ACM Trans. Math. Software 35, Article 16, 2008.
M. Okabe. Full-explicit interpolation formulas for the Argyris triangle. Comput. Methods Appl. Mech. Engrg. 106, n^o 3, p. 381-394, 1993.

Notes et références[modifier | modifier le code]

↑ (en) In memoriam to Professor John H. Argyris, par Thomas J.R. Hughes, J. Tinsley Oden et Manolis Papadrakakis
↑ (en) John H. Argyris

Voir aussi[modifier | modifier le code]

Portail des mathématiques

[1] (en) In memoriam to Professor John H. Argyris, par Thomas J.R. Hughes, J. Tinsley Oden et Manolis Papadrakakis

[2] (en) John H. Argyris

[1]

[2]