Théorème de Pohlke
En général, si on projette, en projection parallèle, un trièdre orthonormé sur un plan P, on obtient un triplet de vecteurs qui engendre le plan.
Réciproquement on a le théorème de Pohlke (de) (1855) : Tout triplet de vecteurs qui engendre un plan P, est l'image, à une homothétie près, d'un trièdre orthonormé par une projection oblique.
Une extension du théorème de Pohlke[modifier | modifier le code]
Soit trois droites concourantes distinctes du plan de projection. Il est facile de construire un triangle dont les trois hauteurs sont les droites portées par les trois droites données. Si l’orthocentre de ce triangle est intérieur au triangle, il existe un trièdre trirectangle qui se projette orthogonalement sur ces trois droites.
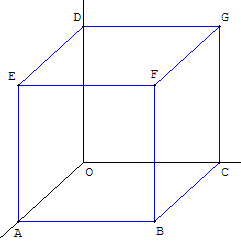
En particulier si A, C et D sont trois points distincts sur les trois droites concourantes en O, alors OACD peut être considéré comme un coin de cube, représentant en perspective cavalière le cube OABCDEFG.
Voir aussi[modifier | modifier le code]
Article connexe[modifier | modifier le code]
Lien externe[modifier | modifier le code]
Application : Quatre cercles de même rayon


