Lame à faces parallèles

Lame à faces parallèles utilisée en laboratoire d'optique atomique.

En optique, une lame à faces parallèles est une pièce taillée dans un matériau homogène, transparent et limitée par deux dioptres plans parallèles entre eux. Dans sa forme la plus simple, la lame à faces parallèles est une vitre de verre. Cet instrument est utilisé pour de nombreuses applications en optique, entre autres en tant que lame séparatrice, miroir dichroïque ou translateur de faisceaux. De plus, la lame à face parallèle est le plus simple des interféromètres. En fonction des applications, la lame peut avoir une ou deux faces traitées (traitement diélectrique ou anti-reflet par exemple).

Contexte

Les composants d’optique classique se présentent tous sous forme de lames. Si les deux dioptres qui limitent la lame sont plats et parallèles entre eux, il s’agit d’une lame à face parallèles. Lorsque l’une des deux faces est sphérique, on a affaire à une lentille plan-concave ou plan-convexe. Il est également possible d’avoir des lentilles cylindriques ou asphériques. Lorsque les deux dioptres sont sphériques, on obtient également une lentille, laquelle peut-être mince ou épaisse. Enfin, une lame dont les deux dioptres limitants ne sont pas parallèles est appelée prisme. D'autres composants présentent des formes un peu plus exotiques, tels que les lentilles à surfaces coniques (axicons) ou les prismes à plus de trois faces (pentaprisme par exemple).

Contrairement aux lentilles, les lames à faces parallèles ne sont généralement pas utilisées en tant que dispositif imageant mais sont présentes dans ces systèmes, sous la forme par exemple de vitre protectrice ou de lame séparatrice.

Optique géométrique

Du point de vue de l'optique géométrique, les lames à faces parallèles sont des lentilles dont les rayons de courbure sont infinis. Les foyers d'un tel système sont rejetés à l'infini, il s'agit donc d'un système afocal.

La lame à faces parallèles est rigoureusement stigmatique pour la conjugaison de deux points situés à l’infini. Cela revient à dire qu’elle n’introduit pas d’aberrations sur des faisceaux collimatés.

De plus, l’image d’un objet à l’infini est superposée avec l’objet lui-même. Les propriétés de la source (monochromatique ou polychromatique) n’ont pas d’influence sur cet effet.

Pour une lame à faces parallèles, un objet et son image sont toujours dans le même espace. Cela signifie que si l’objet est réel, l’image est virtuelle, et vice versa.

Grandissement

Des formules de conjugaison classiques, on obtient ainsi les suivantes:

${\frac {z'}{z}}={\frac {n'}{n}}\Rightarrow g_{y}=1$

Avec $z$ (resp. $z'$) la distance entre l'objet (resp. l'image) et le centre de la lame, et $n$ (resp. $n'$) l'indice de réfraction de l'espace objet (resp. espace image).

Ainsi, la lame à faces parallèles se comporte comme un système afocal dont les deux lentilles auraient la même focale: son grandissement vaut 1. La taille de l'image est la même que celle de l'objet.

Les foyers étant à l'infini, la distance entre l'objet et l'image ne dépend pas de la position de l'objet. C'est l'inclinaison des rayons par rapport aux dioptres qui détermine cette distance.

D'autre part, un point objet et son image sont toujours sur une droite parallèle à l'axe optique.

Déplacement longitudinal

Effet d'une lame à faces parallèles sur un faisceau convergent.

Lorsqu’on introduit une lame à faces parallèles dans un système d’imagerie on observe un déplacement de l’image. Si les faces de la lame sont orthogonales à l’axe optique, la réfraction des rayons dans la lame provoque un déplacement longitudinal de l’image: en insérant la lame entre la source et l’image, on écarte l’image de sa position initiale. L’image est plus loin de la source qu’auparavant.

Dans le cadre de l’approximation paraxiale, l’amplitude du déplacement est directement liée à l’indice de réfraction par la relation:

$\Delta z_{\text{p}}={\frac {n-1}{n}}e$

Avec n l’indice de réfraction de la lame, e son épaisseur, et Δzp la distance entre la position de l’image avec et sans la lame.

Hors de la région paraxiale, la relation précédente devient:

$\Delta z_{\text{m}}=\left(1-{\sqrt {\frac {1-\sin ^{2}(u)}{n^{2}-\sin ^{2}(u)}}}\right)e$

Avec u l’angle entre le rayon incident et la normale aux dioptres.

Cette différence s’explique par la présence d’aberration sphérique. La différence entre le résultat trouvé pour les rayons marginaux et celui trouvé pour les rayons paraxiaux est positive, ce qui signifie que la lame à face parallèles est sur-corrigée en termes d’aberration sphérique. Puisque les lentilles simples sont naturellement sous-corrigées, la combinaison d’un élément simple avec une lame à faces parallèles permet une certaine compensation, laquelle dépend bien sûr de l’amplitude des corrections de chacun des éléments.

Déplacement transversal

Déplacement transversal d'un faisceau collimaté.

Lorsque la lame est inclinée par rapport à l’axe optique, on observe un décalage transversal de l’image, donné par la formule:

$\Delta y=\left(1-{\sqrt {\frac {1-\sin ^{2}(u)}{n^{2}-\sin ^{2}(u)}}}\right)e\sin(u)$

Avec u l’angle d’inclinaison de la lame par rapport à l’axe optique.

Pour les angles faibles, la formule précédente se simplifie en:

$\Delta y={\frac {(n-1)}{n}}e\times u_{\text{p}}=\Delta z_{\text{p}}u_{\text{p}}$

Le décalage transversal du faisceau est directement proportionnel au décalage longitudinal.

Matrices paraxiales

Schéma d'une lame à face parallèle translatant un faisceau collimaté.

Dans le plan méridional (défini par l’axe optique souvent noté z, et un des deux autres axes) un rayon paraxial peut être totalement défini par seulement deux paramètres. D’une part, on choisit de noter x la distance du point de départ de ce rayon par rapport à l’axe optique. D’autre part, on notre φ l’angle qu’il forme avec l’axe optique.

Dans le cas paraxial, l’action d’un composant optique peut être traduite sous forme matricielle grâce aux matrices paraxiales.

La matrice paraxiale d’une lame à faces parallèles s’écrit:

${\begin{pmatrix}x\prime \\\phi \prime \\\end{pmatrix}}={\begin{pmatrix}1&en/n_{l}\\0&n/n\prime \\\end{pmatrix}}{\begin{pmatrix}x\\\phi \\\end{pmatrix}}$

Avec n l’indice du milieu avant la lame, nl l’indice de la lame, et n’ l’indice du milieu après la lame.

Dans le cas où la lame est plongée dans l’air, la matrice devient:

${\begin{pmatrix}x\prime \\\phi \prime \\\end{pmatrix}}={\begin{pmatrix}1&e/n_{l}\\0&1\\\end{pmatrix}}{\begin{pmatrix}x\\\phi \\\end{pmatrix}}$

Aberrations

Les formules des aberrations ne peuvent pas être déduites de celles connues pour les lentilles minces. En effet, dans le calcul de ces aberrations, l’épaisseur de la lentille a été négligée. Il n’est bien sûr pas possible de faire la même simplification dans le cas d’une lame à faces parallèles.

Une lame à faces parallèles n'introduit pas d'aberrations sur un faisceau collimaté. En revanche, lorsque le faisceau est convergent ou divergent, la lame introduit des aberrations importantes. Ces aberrations dépendent toutes linéairement de l'épaisseur de la lame.

Aberrations du troisième ordre

Les rayons issus des objets placés à distance finie de la lame à faces parallèles attaquent le premier dioptre avec un angle d'incidence non nulle, il y a donc présence d'aberrations. En particulier, les lames à faces parallèles présentent de l'aberration sphérique, de l'aberration chromatique et de l'astigmatisme.

Aberrations du troisième ordre dans une lame à faces parallèles

	Expression
Aberration sphérique	${\frac {(n^{2}-1)e}{32n^{3}N^{3}}}$
Coma	${\frac {(n^{2}-1)eu_{p}}{8n^{3}N^{2}}}$
Astigmatisme	${\frac {(n^{2}-1)eu_{p}^{2}}{2n^{3}N}}$
Chromatisme axial	${\frac {(n-1)e}{2n^{2}\nu N}}$
Chromatisme latéral	${\frac {(n-1)eu_{\text{p}}}{n^{2}\nu }}$

Avec n l'indice de réfraction de la lame, e son épaisseur, up l'angle d'incidence du faisceau paraxial par rapport à la normale, N l'ouverture, et nu la constringence.

Les aberrations créées par une lame à faces parallèles sont importantes. Même lorsque la lame est relativement fine, elles ne peuvent généralement pas être négligées. De plus, ces aberrations étant toutes reliées à l’indice optique et à la constringence, le matériau utilisé pour faire ce type de lames doit être choisi avec précaution. En particulier, il convient de choisir des verres de fort indice de réfraction et de faible nombre d’Abbe pour limiter les aberrations. En pratique, ces caractéristiques sont rassemblées dans le verre flint.

Interférométrie

Une lame à faces parallèles est un interféromètre à division d’amplitude. Cela signifie qu’une onde provenant d’une source unique peut être divisée en plusieurs nouvelles ondes qui ont le même front d’onde et dont la somme des amplitudes est égale à l’amplitude de l’onde de départ.

D'autre part, si le coefficient de réflexion est petit, les interférences sont en bonne approximation des interférences à deux rayons. En effet, l’amplitude des rayons suivants est négligeable.

Franges d'égales inclinaison

Schéma de principe des interférences d'une lame à faces parallèles.

Modélisation d'une figure d'interférence présentant des franges d'égale inclinaison.

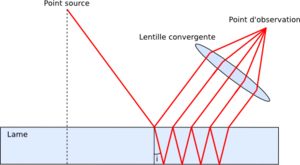
La division d’amplitude se fait grâce aux réflexions et transmissions à chaque dioptre de la lame. Lorsqu’on éclaire la lame avec une source ponctuelle et monochromatique, certains rayons se reflètent à la surface du premier dioptre tandis que certains autres se réfractent et se reflètent à la surface du second dioptre. En conséquence, tout point situé du même côté que la source est illuminé par au moins un rayon qui s’est réfléchi, et au moins un qui s’est réfracté. Les deux rayons étant cohérents entre eux, on observe des interférences.

D’autre part, le phénomène est totalement symétrique par rapport à l’axe orthogonal au dioptre et passant par la source: on s’attend à voir apparaître des cercles de différence de marche constante.

La différence de marche entre deux franges consécutives vaut:

$\delta =2ne\cos(r)\pm {\frac {\lambda }{2}}$

Avec n l’indice de réfraction de la lame, e son épaisseur, r l’angle entre un rayon réfracté et la normale au dioptre et lambda la longueur d’onde.

En théorie des interférences, le déphasage entre deux rayons s’écrit: $\Delta \phi =2\pi \delta /\lambda$. Ainsi:

• Si $\Delta \phi =0[2\pi ]$, l’interférence est constructive, on voit une frange brillante. Ceci est atteint pour $2ne\cos(r)\pm \lambda /2=m\lambda$ avec m un entier relatif.
• Si$\Delta \phi =\pi [2\pi ]$, l’interférence est destructive, on voit une frange noire. Cette situation apparaît lorsque $2ne\cos(r)\pm \lambda /2=(m+1/2)\lambda$.

Les cercles observés sont appelés franges d'égale épaisseur ou franges de Fizeau. Généralement, l'amplitude des différents rayons est très différente, la visibilité des franges est donc réduite.

Franges d'égale inclinaison

Schéma d'une configuration en franges d'égales inclinaison.

Lorsque le coefficient de réflexion est important, des réflexions à multiples faisceaux interviennent. C'est par exemple le cas lorsqu’il y a un revêtement haute réflexion sur les faces de la lame. Tout se passe comme si on avait un interféromètre de Fabry-Perot, à la différence près que les réflexions mises en jeu ne sont pas entre deux lames, mais à l'intérieur de la lame.

Par approximation trigonométrique des petits angles, deux rayons voisins ont également une différence de marche de:

$\delta =2ne\cos(r)\pm {\frac {\lambda }{2}}$

Avec n l’indice de réfraction de la lame, e son épaisseur, r l’angle entre un rayon réfracté et la normale au dioptre et lambda la longueur d’onde.

La distance entre deux longueurs d’onde transmises (Intervalle spectral libre), vaut

$\Delta \lambda ={\frac {\lambda ^{2}}{1+2ne\cos(r)}}$

Dans ce cas, on observe des Franges de Haidinger (en), ou franges d'égale inclinaison.

Applications

Lames séparatrices

Schéma d'une lame séparatrice.

Les lames à faces parallèles sont souvent utilisées comme lames séparatrices. Elles sont notamment présentes dans tous les interféromètres à division d'amplitude. En particulier, elles sont l'élément qui permet de séparer les deux bras de l'interféromètre de Michelson, celui de Mach-Zehnder et celui de Sagnac. Elles apparaissent également dans l'interféromètre de Interféromètre de Jamin (en), et celui de Fabry-Perot.

Dans ce genre de dispositifs, les lames séparatrices sont généralement orientées à 45° par rapport à l’axe optique. Dans le cas d'un faisceau collimaté traversant la lame, on observe un déplacement transversal du faisceau donné par:

$\Delta y_{45}={\dfrac {e}{\sqrt {2}}}\cdot \left(1-(2n^{2}-1)^{-1/2}\right)$

Ce déplacement est d’environ un tiers de l’épaisseur de la lame pour un verre crown standard (n=1.5) et plus de la moitié de l’épaisseur pour du germanium (n=4).

Compensatrice de différence de marche

En optique, on définit le chemin optique comme la distance parcourue par le rayon multipliée par l'indice du matériau traversé.

$\delta =\int _{0}^{L}xn(x){\text{d}}x$

Avec $L$ la distance totale parcourue et $n(x)$ l'indice du matériau à la position $x$. Cette expression devient une simple multiplication lorsque le milieu est homogène.

Les lames à faces parallèles peuvent être utilisées pour modifier le chemin optique. Puisque l'indice du verre est supérieur à celui de l'air, on utilise les lames à face parallèles pour augmenter le chemin optique.

En particulier dans le cadre de l'interférométrie à division d'amplitude, il est nécessaire d'utiliser une lame dite compensatrice pour s'affranchir de l'épaisseur de la lame séparatrice. En effet, lorsqu'un faisceau est séparé à la surface d'une lame, la partie réfléchie ne traverse pas la lame tandis que la partie transmise, elle, la traverse. La lame n'ayant pas le même indice optique que l'air, le chemin optique des deux faisceaux n'est donc plus égal.

Pour corriger cette différence, on place une lame compensatrice devant la lame séparatrice, constituée avec le même verre et ayant la même épaisseur. Les rayons réfléchis et transmis ont ainsi le même chemin optique.

Les franges d'interférences sont directement liées au déphasage entre les deux faisceaux et le déphasage lui-même est lié à la différence de marche ou différence de chemin optique. Ainsi, s'il l'on veut faire des mesures interférométriques quantitatives, il est nécessaire d'utiliser une lame compensatrice de manière que les deux bras de l'interféromètre aient le même chemin optique.

• 
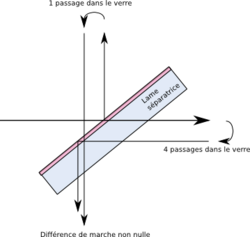
  Lame séparatrice sans compensation: Lorsque les deux rayons se rencontrent (en bas de la figure), le rayon réfléchi n'a traversé qu'une épaisseur de verre tandis que le rayon transmis en a traversé trois: la différence de marche n'est pas nulle.
• 
  Lame séparatrice corrigée par une lame compensatrice: Lorsqu'ils se rencontrent les deux rayons ont traversé quatre épaisseurs de verre chacun: la différence de chemin optique est nulle.
• 
  Un cube séparateur est l'équivalent d'une lame séparatrice et d'une lame compensatrice: il n'a pas besoin de compensatrice supplémentaire.

Micromètre optique

En laboratoire, la lame à faces parallèles est souvent utilisée pour mesurer ou imposer des déplacements transversaux à des faisceau collimatés. Une fois l’indice et l’épaisseur de la lame connus, le déplacement transversal est simplement proportionnel à l’angle d’inclinaison de la lame par rapport à l’axe optique. Afin de disposer d’un réglage sur chacun des deux axes orthogonaux à l’axe optique, il est fréquent de placer à la suite deux lames à faces parallèles dont les axes de rotation sont orthogonaux entre eux. Ce genre de dispositifs peut-être utilisé pour aligner des systèmes optiques lourds: pour éviter de devoir installer toute une partie du montage sur une platine de translation, ce n’est plus les optiques que l’on déplace, mais le faisceau lui-même.

Les lames à faces parallèles sont utilisées comme protection pour les vitres ou filtres. Elles peuvent également être utilisées pour des mesures d'angles au goniomètre.

Miroir dichroïque

Miroirs diélectriques de laboratoire.

Un miroir dichroïque ou filtre dichroïque est une lame à faces parallèles dont l'une des faces a subi un traitement antireflet et l'autre un traitement dichroïque. Ce type de composant permet de faire de la synthèse additive ou de la synthèse soustractive de faisceaux lumineux.

Les miroirs dichroïques sont, à la différence des miroirs diélectriques ou métalliques, des lames à faces parallèles. En effet, une partie du spectre lumineux les traverse et ressort par l'autre face. Ainsi, les contraintes de parallélisme des faces, d'homogénéité du substrat et d'état de surface des deux dioptres sont des éléments importants de la conception de tels filtres.

En pratique, ces miroirs sont utilisés pour filtrer la lumière ou la chaleur. Ils ont l'avantage de ne rien absorber: chaque longueur d'onde est ou bien transmise, ou bien réfléchie, ce qui les rend plus robustes que les filtres à gel classique. Les miroirs dichroïques sont par exemple l'élément clé de la microscopie par fluorescence. Lorsqu'ils filtrent la chaleur (rayonnement infrarouge), on parle alors de filtres chauds ou filtres froids.

Polariseur en réflexion et en transmission

Comme l'ont montré les travaux de Frédéric de La Provostaye et de Paul Desains en 1850, il est possible de construire un polariseur à l’aide de lames à faces parallèles.

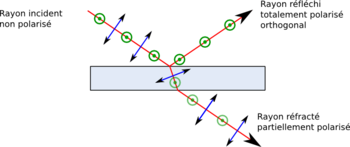
Lorsqu'un rayon lumineux non-polarisé vient heurter une lame de verre à l’angle de Brewster, la lumière est séparée en un faisceau totalement polarisé et un faisceau partiellement polarisé. En effet, pour cet angle particulier, le coefficient de réflexion de la polarisation parallèle au plan d’incidence est nul. Le rayon réfléchi est donc totalement polarisé orthogonalement au plan d’incidence tandis que le rayon transmis est partiellement polarisé. Il reste dans le rayon transmis la polarisation parallèle ainsi qu’un peu de polarisation orthogonale car le coefficient de réflexion ne vaut généralement pas 1.

Un seul dioptre permet donc d’obtenir un rayon réfléchi totalement polarisé, mais ne constitue pas pour autant un polariseur pour la réfraction.

Pour fabriquer un polariseur en transmission, l’idée est de répéter le phénomène en empilant plusieurs lames à faces parallèles. À chaque réflexion, une partie de la polarisation orthogonale est réfléchie, si bien qu’au bout d’un nombre suffisant de dioptres, toute la polarisation orthogonale a été réfléchie et le rayon transmis est entièrement polarisé parallèlement.

Le degré de polarisation peut être calculé de la manière suivante:

$P={\frac {I_{p}-I_{o}}{I_{p}+I_{o}}}={\frac {m}{m+{\frac {2n^{2}}{1-n^{2}}}}}$

Avec Ip l’intensité du faisceau polarisé parallèlement au plan d’incidence, Io celle du faisceau polarisé orthogonalement, n l’indice des lames de verre, et m le nombre de lames.

Il est intéressant de noter que l’angle de Brewster dépend de l’indice optique, si bien qu’il est nécessaire que les lames aient rigoureusement le même indice optique. En revanche, le phénomène est totalement indépendant de l’épaisseur des lames.

• 
  Effet d'une lame à faces parallèles sur un faisceau lumineux à l'incidence de Brewster.
• 
  L'utilisation de plusieurs lames successives permet de polariser totalement un faisceau non-polarisé. Un faisceau totalement polarisé orthogonal est réfléchi tandis qu'un faisceau totalement polarisé parallèle est réfléchi.

Cette méthode est particulièrement adaptée pour les petites corrections de défauts de polarisation car elle fait dans ce cas appel à un faible nombre de lames.

Ce procédé n'est pas très efficace lorsqu'on cherche à créer un polariseur total en transmission. En effet, le composant est alors très sensible aux défauts d'alignements entre les lames. De plus, les réflexions multiples impliquent une grande perte d'énergie: les pertes par insertion de ce composant sont très élevées. Pour ces raisons, les polariseurs actuels sont dans la majorité réalisés avec des filtres polaroïds.

Annexes

Articles connexes

• Miroir semi-réfléchissant
• Interférométrie
• Optique géométrique
• Miroir dichroïque

Ouvrages de référence

 : document utilisé comme source pour la rédaction de cet article.

• (en) Francis Jenkins et Harvey White, Fundamentals of Optics, McGraw-Hill Science/Engineering/Math, 2001 (ISBN 978-0072561913)
• (en) Max Born et Emil Wolf, Principles of Optics, Cambridge University Press, 1999 (ISBN 978-0521642224)

Liens externes

• (en) Un calculateur d'aberrations sphériques pour lame à faces parallèles