Intégrale de Fresnel

L'intégrale de Fresnel est une intégrale impropre introduite par le physicien français Augustin Fresnel.

Formule de Fresnel

Les fonctions S(x) et C(x) non normalisées.

$\int _{0}^{+\infty }\cos(t^{2})~\mathrm {d} t=\int _{0}^{+\infty }\sin(t^{2})~\mathrm {d} t={\frac {1}{2}}{\sqrt {\frac {\pi }{2}}}.$

Ces égalités sont équivalentes à l'expression de l'intégrale de Fresnel complexe (par identification des parties réelle et imaginaire dans un sens et par combinaison linéaire dans l'autre) :

$\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}\,\mathrm {d} t={\sqrt {\dfrac {\pi }{2}}}{\dfrac {1-\mathrm {i} }{2}}.$

Convergence de l'intégrale

Le calcul explicite (voir infra) montrera que l'intégrale de Fresnel converge, mais on peut s'en assurer plus simplement :

• par le changement de variable s = t², la convergence de $\int _{1}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}~\mathrm {d} t$ équivaut à celle de $\int _{1}^{+\infty }{\frac {\mathrm {e} ^{-\mathrm {i} s}}{s^{1/2}}}~\mathrm {d} s$ ;
• d'après la règle d'Abel, pour tout λ > 0, l'intégrale $\int _{1}^{+\infty }{\frac {\mathrm {e} ^{-\mathrm {i} s}}{s^{\lambda }}}~\mathrm {d} s$ converge.

Définition

Les fonctions S(x) et C(x) normalisées.

Les fonctions de Fresnel sont des fonctions spéciales, définies par les intégrales et développement en série entière associés :

$S(x)=\int _{0}^{x}\sin(t^{2})\,\mathrm {d} t=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+3}}{(2n+1)!(4n+3)}},$

$C(x)=\int _{0}^{x}\cos(t^{2})\,\mathrm {d} t=\sum _{n=0}^{\infty }(-1)^{n}{\frac {x^{4n+1}}{(2n)!(4n+1)}}.$

Ces fonctions sont parfois définies avec l'argument π/2t² dans les intégrales définissant S(x) et C(x). Les intégrales sont alors multipliées par ${\sqrt {\frac {2}{\pi }}}$ et les intégrandes sont divisés par x.

La formule de Fresnel vue précédemment est donc la limite en +∞ des deux fonctions S et C non normalisées.

Calcul de l'intégrale de Fresnel

Parmi les diverses méthodes, en voici deux : la première utilise la technique de Feynman, la seconde repose sur les intégrales de contour.

Par une intégrale à paramètre

On considère pour tout réel t la fonction de ℝ⁺ dans ℂ définie par

$u\mapsto {\mathrm {e} ^{-(u^{2}+\mathrm {i} )t^{2}} \over u^{2}+\mathrm {i} }.$

Cette fonction est intégrable, car continue sur ℝ⁺ et majorée en module par $u\mapsto {\tfrac {1}{u^{2}}}$, qui est intégrable en +∞.

Il est donc possible de poser f, la fonction définie pour tout t par l'intégrale à paramètre suivante :

$f(t)=\int _{0}^{+\infty }{\frac {\mathrm {e} ^{-(u^{2}+\mathrm {i} )t^{2}}}{u^{2}+\mathrm {i} }}~\mathrm {d} u.$

On montre que f est continue sur ℝ et nulle à l'infini, et qu'elle est de classe C¹ sur ℝ⁺* avec

$\forall t\in \mathbb {R} ^{+*},~f'(t)=-2t\mathrm {e} ^{-\mathrm {i} t^{2}}\int _{0}^{+\infty }\mathrm {e} ^{-u^{2}t^{2}}\mathrm {d} u.$

Démonstration

On applique le théorème de convergence dominée.

• Continuité sur ℝ et nullité à l'infini
  • Pour tout u ∈ ℝ⁺*, la fonction $\mathbb {R} \rightarrow \mathbb {C} ,\ t\mapsto {\mathrm {e} ^{-(u^{2}+\mathrm {i} )t^{2}} \over u^{2}+\mathrm {i} }$ est continue et nulle à l'infini.
  • Pour tout réel t, la fonction $\mathbb {R} ^{+}\rightarrow \mathbb {C} ,\ u\mapsto {\mathrm {e} ^{-(u^{2}+\mathrm {i} )t^{2}} \over u^{2}+\mathrm {i} }$ est continue donc mesurable.
  • Condition de domination : $\forall (t,u)\in \mathbb {R} \times \mathbb {R} ^{+},~\left|{{\mathrm {e} ^{-(u^{2}+\mathrm {i} )t^{2}}} \over {u^{2}+\mathrm {i} }}\right|\leq {\frac {1}{\sqrt {1+u^{4}}}}$ et la fonction $u\mapsto {\tfrac {1}{\sqrt {1+u^{4}}}}$ est intégrable sur ℝ⁺.
  • Conclusion : $f$ est continue sur ℝ et nulle à l'infini.
• Classe C¹ sur ℝ⁺* et valeur de la dérivée.
  • Pour tout u ∈ ℝ⁺, la fonction $\mathbb {R} ^{+*}\rightarrow \mathbb {C} ,\ t\mapsto {\mathrm {e} ^{-(u^{2}+\mathrm {i} )t^{2}} \over u^{2}+\mathrm {i} }$ est dérivable et sa dérivée, $\mathbb {R} ^{+*}\rightarrow \mathbb {C} ,\ t\mapsto -2t\exp {[-(u^{2}+\mathrm {i} )t^{2}]},$ est continue.
  • Pour tout t ∈ ℝ⁺*, la fonction $\mathbb {R} ^{+}\rightarrow \mathbb {C} ,\ u\mapsto -2t\exp {[-(u^{2}+\mathrm {i} )t^{2}]}$ est mesurable.
  • Condition de domination : confinons le paramètre $t$ à l'intervalle $]a,b[$ avec $0<a<b$. $\forall (t,u)\in ]a,b[\times \mathbb {R} ^{+},~\left|-2t\exp {[-(u^{2}+\mathrm {i} )t^{2}]}\right|\leq 2b~\mathrm {e} ^{-u^{2}a^{2}}$ et la fonction $u\mapsto 2b~\mathrm {e} ^{-u^{2}a^{2}}$ est intégrable sur ℝ⁺.
  • Conclusion : $f$ est de classe $C^{1}$ sur ℝ⁺* et

$\forall t\in \mathbb {R} ^{+*},~f'(t)=-2t\mathrm {e} ^{-\mathrm {i} t^{2}}\int _{0}^{+\infty }\mathrm {e} ^{-u^{2}t^{2}}\mathrm {d} u.$

En simplifiant l'expression de f' et en l'intégrant de 0 à +∞, on en déduit que

$\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}~\mathrm {d} t={\frac {1}{\sqrt {\pi }}}\int _{0}^{+\infty }{\frac {1}{u^{2}+\mathrm {i} }}~\mathrm {d} u.$

Démonstration

Le changement de variable v = ut donne, pour tout t ∈ ℝ⁺* :

$f'(t)=-2\mathrm {e} ^{-\mathrm {i} t^{2}}\int _{0}^{+\infty }\mathrm {e} ^{-v^{2}}~\mathrm {d} v.$

L'intégrale définie est l'intégrale de Gauss, qui vaut ${\tfrac {\sqrt {\pi }}{2}}$. Ainsi, on a une expression plus simple de la dérivée de f :

$f'(t)=-{\sqrt {\pi }}\mathrm {e} ^{-\mathrm {i} t^{2}}$.

Par conséquent :

$0-\int _{0}^{+\infty }{\frac {1}{u^{2}+\mathrm {i} }}~\mathrm {d} u=\left(\lim _{t\to +\infty }f(t)\right)-f(0)=\int _{0}^{+\infty }f'(t)~\mathrm {d} t=-{\sqrt {\pi }}\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}~\mathrm {d} t.$

On se sert alors de l'expression ${\textstyle {\frac {1}{u^{2}+\mathrm {i} }}}$ sous la forme ${\textstyle {\frac {u^{2}-\mathrm {i} }{u^{4}+1}}}$ et d'une intégrale classique :

$\int _{0}^{+\infty }{u^{2} \over u^{4}+1}~\mathrm {d} u=\int _{0}^{+\infty }{1 \over u^{4}+1}~\mathrm {d} u={\frac {\pi }{2{\sqrt {2}}}}$

pour en déduire que

$\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}~\mathrm {d} t={\sqrt {\frac {\pi }{2}}}{\dfrac {1-\mathrm {i} }{2}}$.

Démonstration

D'après ce qui précède, ${\textstyle \int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}~\mathrm {d} t={\frac {I-\mathrm {i} J}{\sqrt {\pi }}}}$ avec $I=\int _{0}^{+\infty }{\frac {u^{2}}{u^{4}+1}}~\mathrm {d} u$ et $J=\int _{0}^{+\infty }{1 \over u^{4}+1}~\mathrm {d} u$.

Or d'une part I = J (par le changement de variable v = 1/u) et d'autre part,

${\frac {2(u^{2}+1)}{u^{4}+1}}={\frac {1}{u^{2}-u{\sqrt {2}}+1}}+{\frac {1}{u^{2}+u{\sqrt {2}}+1}}$

donc (cf. Primitives de fonctions rationnelles)

$2(I+J)={\sqrt {2}}\left[\arctan(u{\sqrt {2}}-1)+\arctan(u{\sqrt {2}}+1)\right]_{0}^{+\infty }=\pi {\sqrt {2}}$.

Par conséquent, $I=J={\frac {\pi }{2{\sqrt {2}}}}$ et $\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}~\mathrm {d} t={\frac {1-\mathrm {i} }{\sqrt {\pi }}}{\frac {\pi }{2{\sqrt {2}}}}={\sqrt {\dfrac {\pi }{2}}}{\dfrac {1-\mathrm {i} }{2}}$.

Par intégration complexe

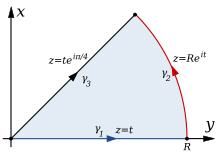
Il est aussi possible d'intégrer $f(z)=\exp(-z^{2})$ sur le bord du secteur circulaire $T_{R}$ de sommets $0,~R,~{\frac {1}{\sqrt {2}}}(1+\mathrm {i} )~R$ puis de faire tendre $R$ vers l'infini.

Contour utilisé pour le calcul.

$\oint f(z)\,\mathrm {d} z=\underbrace {\int _{0}^{R}\mathrm {e} ^{-t^{2}}\,\mathrm {d} t} _{I_{1}(R)}+\underbrace {\int _{0}^{\pi /4}\mathrm {i} R\,\mathrm {e} ^{\mathrm {i} t}\,\mathrm {e} ^{-R^{2}\exp(2\mathrm {i} t)}\,\mathrm {d} t} _{I_{2}(R)}-\underbrace {\int _{0}^{R}\mathrm {e} ^{\mathrm {i} {\frac {\pi }{4}}}\,\mathrm {e} ^{-\mathrm {i} t^{2}}\,\mathrm {d} t} _{I_{3}(R)}$

Intéressons nous d'abord à I₂.

$|I_{2}(R)|\leq \int _{0}^{\pi /4}R\,\mathrm {e} ^{-R^{2}\cos(2t)}\,\mathrm {d} t=\int _{0}^{\pi /2}{\dfrac {R}{2}}\,\mathrm {e} ^{-R^{2}\cos u}\,\mathrm {d} u$

après un changement de variable u = 2t. Or, sur $\left[0,{\dfrac {\pi }{2}}\right]$, la concavité de cos donne

$\forall u\in \left[0,{\dfrac {\pi }{2}}\right],\quad 1-{\dfrac {2}{\pi }}u\leq \cos u\leq 1$

donc

$\forall u\in \left[0,{\dfrac {\pi }{2}}\right],\quad \mathrm {e} ^{-R^{2}\cos u}\leq \,\mathrm {e} ^{R^{2}\left({\frac {2}{\pi }}u-1\right)}$

donc

$\int _{0}^{\pi /2}{\dfrac {R}{2}}\,\mathrm {e} ^{-R^{2}\cos u}\,\mathrm {d} u\leq {\dfrac {\pi }{4R}}\left(1-\mathrm {e} ^{-R^{2}}\right)$

Le théorème des gendarmes donne ainsi $\lim _{R\rightarrow +\infty }I_{2}(R)=0$. Grâce au résultat de l'intégrale de Gauss, $\lim _{R\rightarrow +\infty }I_{1}(R)={\dfrac {\sqrt {\pi }}{2}}$. De plus, $\lim _{R\rightarrow +\infty }I_{3}(R)=\mathrm {e} ^{\mathrm {i} {\frac {\pi }{4}}}\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}\,\mathrm {d} t$.

La fonction f est entière donc le théorème intégral de Cauchy assure que $\oint f(z)\,\mathrm {d} z=0.$

Dès lors,

$\mathrm {e} ^{\mathrm {i} {\frac {\pi }{4}}}\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}\,\mathrm {d} t={\dfrac {\sqrt {\pi }}{2}}$

donc

$\int _{0}^{+\infty }\mathrm {e} ^{-\mathrm {i} t^{2}}\,\mathrm {d} t=\mathrm {e} ^{-\mathrm {i} {\frac {\pi }{4}}}{\dfrac {\sqrt {\pi }}{2}}={\sqrt {\dfrac {\pi }{2}}}{\dfrac {1-\mathrm {i} }{2}}$.

Remarque

Un calcul identique montre que plus généralement, pour tout nombre complexe β dont la partie réelle appartient à [0 ; 1[,

$\int _{0}^{+\infty }t^{\beta }\mathrm {e} ^{-\mathrm {i} t^{2}}\,\mathrm {d} t=\mathrm {e} ^{-\mathrm {i} {\frac {\pi }{4}}(\beta +1)}{\dfrac {\Gamma \left({\frac {\beta +1}{2}}\right)}{2}},$

où Γ désigne la fonction gamma. En adaptant le choix du contour, on peut même démontrer cette égalité pour $\mathrm {Re} (\beta )\in \left]-1,1\right[$, ce qui, par changement de variable (voir supra), équivaut au calcul du § « Exemple » de l'article sur le théorème intégral de Cauchy.

Articles connexes

• Clothoïde
• Théorie de la diffraction
• Diffraction de Fresnel