Intégration par changement de variable
En mathématiques, et plus précisément en analyse, l’intégration par changement de variable est un procédé d'intégration qui consiste à considérer une nouvelle variable d'intégration, pour remplacer une fonction de la variable d'intégration initiale. Ce procédé est un des outils principaux pour le calcul explicite d'intégrales. Il est parfois appelé intégration par substitution en lien avec le nom anglais du procédé.
Méthode[modifier | modifier le code]
Pour calculer une intégrale , la méthode de changement de variable consiste à poser de telle sorte que le théorème suivant conduise à une nouvelle intégrale plus facile à calculer ( et ).
Théorème[modifier | modifier le code]
Soient :
- I un intervalle réel ;
- φ : [a,b] → I une fonction dérivable, de dérivée intégrable ;
- f : I → R une fonction continue.
Alors,
Remarquons qu'il n'est pas nécessaire que φ soit injective sur (voir infra).
Démonstration[modifier | modifier le code]
Lorsque φ est de classe C1, cette règle d'intégration se déduit du théorème fondamental de l'analyse et du théorème de dérivation des fonctions composées : voir par exemple le lien en bas de cette page vers le cours sur Wikiversité.
Soient :
- I un intervalle réel ;
- φ : [a,b] → I une fonction dérivable de classe C1, de dérivée intégrable ;
- f : I → R une fonction continue.
Notons F une primitive de f sur [a,b], comme f est continue, F est de classe C1 donc est de classe C1 sur [a,b] et :
On obtient en intégrant entre a et b :
Remarque[modifier | modifier le code]
Utilisons le théorème pour écrire l'intégrale de f sur dans le cas où φ est une fonction monotone.
- Si φ est croissante, alors et I est égal à l'intervalle ; l'intégrale de f sur I est alors immédiatement donnée par le théorème. Remarquons aussi que dans ce cas, .
- Si φ est décroissante, alors et I devient . L'intégrale de f sur I est donc l'opposée de l'intégrale du membre de gauche du théorème. Comme , changer le signe revient dans ce cas à remplacer φ' (dans l'intégrale du membre de gauche du théorème) par sa valeur absolue.
On voit ainsi que dans les deux cas on a :
- .
C'est cette formule qu'on peut généraliser au cas des intégrales multiples (voir infra).
Exemple[modifier | modifier le code]
Soit à calculer
- .
On choisit le changement de variable , et donc avec variant de à (on remarquera que n'est pas injective sur cet intervalle)
, , et est bien continue sur . Par conséquent :
- .
Le fait que ne soit pas injective peut amener à des résultats à première vue surprenants : si , on aura ; c'est la raison pour laquelle on préfère souvent prendre bijective, et écrire la formule « dans l'autre sens » : .
Changements de variables classiques[modifier | modifier le code]
En pratique, la forme donnée dans l'énoncé du théorème est rarement directement lisible sur l'intégrale à calculer, et partant d'une intégrale telle que , on essaie plutôt de faire disparaitre les termes les plus « compliqués » (les exponentielles, dans ce cas) en posant , avec bien choisi (et le plus souvent bijective), donc ici ; on obtient , que l'on intègre ensuite par décomposition en éléments simples, obtenant .
Cependant, beaucoup d'intégrales ne peuvent se calculer qu'à l'aide de changements de variables plus sophistiqués ; en voici une liste non exhaustive.
Homothéties[modifier | modifier le code]
La bijection , pour donne
- .
Règle de Bioche[modifier | modifier le code]
Pour les fonctions comportant des fonctions circulaires ou hyperboliques, on peut utiliser les règles de Bioche.
Substitution d'Euler[modifier | modifier le code]
Pour calculer
- où f est une fraction rationnelle en deux variables, n un entier naturel et a, b, c et d quatre réels donnés, on pose
:
le changement de variable donnera toujours une fraction rationnelle en u ; il suffit alors de la décomposer en éléments simples pour intégrer.
Pour calculer
où f est une fraction rationnelle en deux variables, Euler a proposé le changement de variable , qui donne lui aussi toujours une fraction rationnelle en t (le cas peut également être ainsi traité, si l'on accepte de travailler dans les complexes, il faut sinon passer par les fonctions circulaires (en)).
Substitution de Weierstrass[modifier | modifier le code]

La substitution de Weierstrass repose sur la formule du demi-angle, qui transforme une fraction rationnelle de fonctions trigonométriques en x en fonctions rationnelles classiques en t, par le changement de variables t = tan (x2) :
On peut l'adapter aux fractions rationnelles de fonctions hyperboliques en x en fonctions rationnelles classiques en t, par le changement de variables t = tanh (x2) :
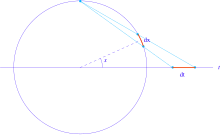
Géométriquement, ces changements de variables se traduisent par la projection vers une droite du cercle trigonométrique (pour les fonctions trigonométriques) ou le disque de Poincaré en dimension 1 (pour les fonctions hyperboliques).
Cas des intégrales impropres[modifier | modifier le code]
Les formules données précédemment sont en fait valables même si les intégrales sont impropres[1], ce qui se produit en particulier lorsque le changement de variable fait passer d'un intervalle réel borné à un intervalle non borné (par exemple, l'intégrale devient, par le changement de variable , ).
La démonstration de ce résultat se fait simplement en appliquant la définition des intégrales impropres comme limites, donc en passant à la limite dans un changement de variable entre intégrales propres.
Cas des intégrales multiples[modifier | modifier le code]
Lorsque f est une fonction de plusieurs variables, on remplace φ par une injection de classe C1 sur un ouvert U de ℝn et à valeurs dans ℝn. Outre le changement du domaine d'intégration, on utilise la valeur absolue du jacobien de « à la place » de . Le jacobien est le déterminant de la matrice jacobienne . On donne ici la formulation explicite du changement de variable dans le cas particulier n = 2 :
- .
Pour plus de précision, se reporter aux deux articles détaillés.
Note[modifier | modifier le code]
- On en trouvera de nombreux exemples dans .
Voir aussi[modifier | modifier le code]
Lien externe[modifier | modifier le code]
Autre exemple bien détaillé d'intégration par changement de variable







![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle \int _{\varphi {(a)}}^{\varphi {(b)}}f(x)\,\mathrm {d} x=[F(x)]_{\varphi {(a)}}^{\varphi {(b)}}=[F(\varphi {(t)})]_{a}^{b}=\int _{a}^{b}(F\circ \varphi )^{\prime }(t)\,\mathrm {d} t=\int _{a}^{b}f(\varphi (t))\varphi '(t)~\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07501fdb0d25c926eeae3c2eda9a63c540e7091c)
![{\displaystyle I=\varphi {\bigl (}[a,b]{\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8b9a559281d3571275e00b121074e8bb796b6b7)

![{\displaystyle [\varphi (a),\varphi (b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4a4c2a63e663a69830c8fb57a13d4273787148)


![{\displaystyle [\varphi (b),\varphi (a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e4e8891eae1180434cfab14f935fb1027ef7e79)

![{\displaystyle \int _{\varphi {\bigl (}[a,b]{\bigr )}}f(x)\,\mathrm {d} x=\int _{[a,b]}f(\varphi (t))|\varphi '(t)|\,\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6893f396132370be777a21d54421392cd24ba285)










![{\displaystyle \varphi \left(\left[-{\sqrt {\pi /2}},{\sqrt {2\pi }}\right]\right)=[0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c282a509c1089135647a2f56a3249a6eb386d3)
![{\displaystyle \int _{-{\sqrt {\pi /2}}}^{\sqrt {2\pi }}2t\cos(t^{2})\,\mathrm {d} t=\int _{-{\sqrt {\pi /2}}}^{\sqrt {2\pi }}\varphi '(t)\cos(\varphi (t))\,\mathrm {d} t=\int _{\pi /2}^{2\pi }\cos x\,\mathrm {d} x=\left[\sin x\right]_{\pi /2}^{2\pi }=0-1=-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eab1ebc9c809935e010914fffb7901b742ea1b4a)










![{\displaystyle \int f\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)\,\mathrm {d} x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/061459a77552dd75b1dcc7d91f41e5d368a7ab11)
![{\displaystyle u={\sqrt[{n}]{\frac {ax+b}{cx+d}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85c6dab8107f08d3f4aff52530b7c762cc9923dc)











