Effet magnéto-optique

L'effet magnéto-optique correspond à une modification de la propagation d'une onde électromagnétique dans un matériau sous l'effet d'un champ magnétique.

Une onde électromagnétique est composée d'une onde magnétique et d'une onde électrique en phase et de vecteur polarisation perpendiculaire. L'onde électromagnétique a une distribution en fréquence très large qui contient la totalité des fréquences lumineuses. L'effet magnéto-optique correspond à la modification de la polarisation de cette onde électromagnétique lorsque celle-ci entre en contact avec un matériau plongé dans un champ magnétique quasi statique. Il résulte d'une résonance ferromagnétique.

Les effets les plus utilisés sont l'effet Faraday et l'effet Kerr mis au profit des domaines comme les télécommunications optiques, le stockage de l'information, la visualisation ou les capteurs.

Effet Faraday

Faraday fut le premier à observer l'influence d'un champ magnétique sur la lumière qui traverse un matériau transparent. Lorsque l’on fait passer un rayon lumineux à travers un polariseur, le champ électrique de la lumière en sortie du polariseur est « filtré », pour ne plus apparaître que comme une composante oscillante, fixe dans l’espace le long d’une droite : on parle de polarisation linéaire de la lumière. Lors de la transmission d'une lumière polarisée linéairement dans un matériau transparent attaquant celui-ci sous incidence normale (perpendiculairement à la surface), le plan de polarisation de cette lumière tourne d'un certain angle en présence d'un champ magnétique parallèle à la direction de propagation (effet Faraday, 1846).

L'effet Faraday est notamment utilisé en astrophysique et en cosmologie pour mesurer des champs magnétiques.

Effet Faraday : rotation de l'orientation du champ électrique sous champ magnétique

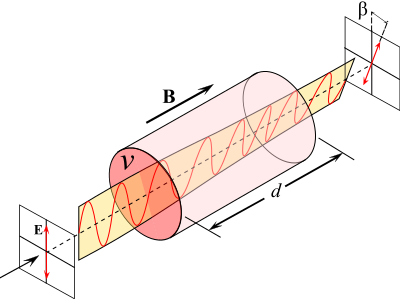
On peut observer au début du schéma ci-dessous (à gauche) le champ électrique qui est devenu vertical en sortie du polariseur optique d'entrée (vecteur E).

Schématisation de l'effet Faraday

À droite, on remarque que lors de la traversée, cette direction a tourné d'un angle bêta.

L'expérience donne l'équation suivante :

$\beta ={\mathcal {V}}\;d\;B$

avec :

β : angle de déviation (rad)

d : distance traversée par l'onde dans le matériau (m)

${\mathcal {V}}$ : constante de Verdet (rad.m^-1.T^-1)

B : représente l'aimantation du matériau (T)

Cette rotation est induite par la modification de la biréfringence du matériau transparent. Cette biréfringence est modifiée par l'effet du champ magnétique de manière non isotrope, cela signifie que la biréfringence varie dans l'espace du matériau. La biréfringence est liée à l'indice de réfraction du matériau noté le plus souvent n.

L'effet Faraday : rotation (due à la présence d'un champ magnétique) d'une polarisation rectiligne.

Constante de Verdet (rad.T^-1.m^-1)

La constante de Verdet caractérise la force de l'effet Faraday. Elle quantifie la variation de l'angle de polarisation de l'onde lumineuse pour un champ magnétique donné. C'est une constante optique qui est difficile à obtenir de par les nombreux paramètres qui influent sa grandeur. Elle varie en fonction de la longueur d'onde, de la température et du matériau. C'est une constante faible dont la valeur est maximale pour les matériaux paramagnétiques ou certains composés du terbium. En plaçant un échantillon de ce matériau dans un champ magnétique fort, une rotation de la polarisation de 45° peut être atteinte. Cela permet la construction d'un rotateur de Faraday. La constante de Verdet est de l'ordre de -100 rad.T^-1.m^-1.

Milieu interstellaire

L'effet Faraday est ressenti par les ondes électromagnétiques dans les milieux interstellaires. Cependant la relation liant la variation de l'angle de polarisation est bien plus simple. Cette variation est proportionnelle au carré de la longueur d'onde de l'onde concernée.

$\beta =\alpha \;\lambda ^{2}\,$

où la constante $\alpha$ dépend du champ magnétique B, de la distance parcourue d, et de la densité d'électrons $n_{e}$ par :

$\alpha ={\frac {e^{3}}{2\pi m^{2}c^{4}}}\int _{0}^{d}n_{e}B\;\mathrm {d} s$

avec:

e la charge de l'électron,

m la masse de l'électron,

et c la vitesse de la lumière dans le vide.

Cette rotation est un outil important en astronomie pour la mesure de champs magnétiques, qui peuvent être estimés à partir de cette rotation lorsqu'on connaît la densité des électrons.

Les ondes radio traversant l'ionosphère de la Terre sont aussi sujettes à l'effet Faraday. Celui-ci étant alors également proportionnel au carré de la longueur d'onde.

Effet Kerr magnéto-optique

Théorie et principe de l'effet Kerr magnéto-optique

Généralités sur l'effet Kerr

L’effet Kerr magnéto-optique est le résultat d’une interaction entre une onde électromagnétique (la lumière par exemple) et un matériau ferromagnétique.

L’effet Kerr est un phénomène électromagnétique très proche de l’effet Faraday. Lorsqu’une onde électromagnétique interagit avec un matériau aimanté (généralement un ferromagnétique) la polarité de l’onde réfléchie n’est pas la même que celle de l’onde incidente, c’est ce que l’on appelle l’effet Kerr. On retrouve le même phénomène lorsque l’onde est transmise par le matériau, c’est ce que l’on appelle l’effet Faraday.

Lorsqu’une onde est réfléchie sur un matériau ferromagnétique aimanté, les différents domaines magnétiques de celui-ci vont influencer la polarisation de l’onde.

Remarque: la réflexion entraîne également une diminution de l’amplitude de l’onde.

On aura donc une polarisation différente entre l’onde incidente et l’onde réfléchie par le matériau. Celui-ci a donc des propriétés optiques de biréfringence.

Réflexion d'une onde polarisée sur un matériau ferromagnétique

Ce phénomène dépend de plusieurs paramètres : la polarisation initiale de l’onde électromagnétique, l’aimantation et l’épaisseur du matériau. On a donc plusieurs configurations possibles pour générer ce phénomène :

• Configuration polaire : l’onde incidente arrive perpendiculairement à la surface de l’échantillon et l’aimantation est elle aussi perpendiculaire à l’échantillon
• Configuration longitudinale : l’onde est dirigée en incidence rasante avec la surface de l’échantillon. L’aimantation est alignée avec la direction de l’onde incidente.
• Configuration transverse : l’onde est dirigée en incidence rasante avec la surface de l’échantillon. L’aimantation est perpendiculaire à la direction de l’onde incidente.

Les différentes configurations de l'effet Kerr

Pour orienter les domaines magnétiques du matériau, on le soumet à un champ magnétique. Les moments magnétiques microscopiques vont s’aligner avec ce champ et on aura une aimantation de l’échantillon dans la même direction que celui-ci.

Théorie de l'effet Kerr

L’effet Kerr a lieu lorsqu’une onde électromagnétique est réfléchie sur un milieu magnétique. On doit donc tenir compte de l’aimantation du matériau ainsi que de la distance de pénétration de l’onde dans celui-ci : d = 4πk où k est le coefficient d’absorption. Dans le cas d’un matériau ferromagnétique soumis à un champ magnétique extérieur, le milieu est magnétiquement ordonné. Le champ est uniquement présent pour orienter ou saturer l’aimantation selon une direction. On ne tiendra donc pas compte de sa présence.

Lorsque l’aimantation du milieu est quelconque l’effet Kerr n’apparaît pas, il faut pour cela se placer dans une des 3 configurations présentées précédemment chacune ayant une approche théorique différente.

Pour cela on doit d’abord considérer les ondes électromagnétiques comme étant polarisées circulairement (cf polarisation circulaire), avec une composante circulaire droite (signe +) et une composante circulaire gauche (signe -). La présence des effets de biréfringence induit des indices de réflexions différents pour la composante gauche et droite. On introduit la notion d’indice optique complexe :

n = n + jk , avec n: indice optique réel, k : coefficient d’absorption du matériau et j le nombre complexe tel que $j^{2}=-1$.

Ainsi que la notion d’indice de réfraction complexe. Celui-ci est propre à chaque composante circulaire et s’exprime d’après les équations de Fresnel de la manière suivante:

Polarisation polaire

Sous incidence normale

On considère une onde incidente polarisée rectilignement, dont les deux composantes (gauche et droite) sont d’amplitude égale et de sens de rotation opposé. Lorsqu’elle est réfléchie, la différence entre les indices de réflexion r+ et r- entraîne une variation hétérogène des amplitudes des composantes circulaires. L’onde réfléchie est désormais polarisée elliptiquement.

différents types de polarisation

On a :

Onde incidente:

$E_{i}=E_{+}+E_{-}$ avec $E_{+}=E_{0}.cos(w_{+}.t)$ et $E_{-}=E_{0}.cos(w_{-}.t)$

Onde réfléchie:

$E_{r}=r_{+}.E_{+}+r_{-}.E_{-}$

• Remarque : Ce formalisme n’est valable qu’en configuration polaire puisqu’on ne peut pas avoir d’incidence normale en longitudinale ou en transverse.

Sous incidence oblique

Dans cette configuration il faut considérer la polarisation d'une l’onde électromagnétique différemment. On la sépare maintenant en 2 nouvelles composantes: une perpendiculaire au plan d’incidence (s) et l’autre colinéaire au plan d’incidence (p).

On a donc $E_{i}=E_{ip}+E_{is}$ et $E_{r}=E_{rp}+E_{rs}$

On doit définir de nouveaux coefficients de réflexion tel que:

${\binom {E_{rp}}{E_{rs}}}={\begin{bmatrix}r_{pp}&r_{ps}\\r_{sp}&r_{ss}\end{bmatrix}}.{\binom {E_{ip}}{E_{is}}}$

Représentation des différentes composantes de polarisation

$r_{pp}={\frac {n_{0}\gamma -\gamma '}{n_{0}\gamma +\gamma '}}$

$r_{ss}={\frac {\gamma -n_{0}\gamma '}{\gamma +n_{0}\gamma '}}$

$r_{sp}=r_{ps}={\frac {\chi _{xy}}{n_{0}(\gamma +n\gamma ')(n_{0}\gamma +\gamma ')}}$

avec $\gamma =cos(\theta _{0})$ , $\gamma '={\sqrt {\frac {1-sin^{2}\theta _{0}}{n_{0}^{2}}}}$ si $\theta _{0}$ est l'angle d'incidence et $\chi _{xy}$ la composante xy du tenseur de susceptibilité électrique.

Polarisation longitudinale

Dans le cas d'une polarisation longitudinale, on se trouve obligatoirement dans le cas d'une polarisation oblique. Le formalisme est le même que pour la configuration polaire sous incidence oblique avec de nouveaux coefficients de réflexion :

${\binom {E_{rp}}{E_{rs}}}={\begin{bmatrix}r_{pp}&r_{ps}\\r_{sp}&r_{ss}\end{bmatrix}}.{\binom {E_{ip}}{E_{is}}}$ avec

$r_{pp}={\frac {n_{0}\gamma -\gamma '}{n_{0}\gamma +\gamma '}}$

$r_{ss}={\frac {\gamma -n_{0}\gamma '}{\gamma +n_{0}\gamma '}}$

$r_{sp}=-r_{ps}={\frac {\chi _{xy}.sin(2\theta _{0})}{2\gamma '{n}_{0}^{2}({n}_{0}\gamma +\gamma ')(\gamma +{n}_{0}\gamma ')}}$

avec $\gamma =cos(\theta _{0})$ , $\gamma '={\sqrt {\frac {1-sin^{2}\theta _{0}}{n_{0}^{2}}}}$ si $\theta _{0}$ est l'angle d'incidence et $\chi _{xy}$ la composante xy du tenseur de susceptibilité électrique.

Polarisation transverse (ou équatoriale)

Dans ce cas on définit de nouveaux indices optiques pour les composantes p et s de l'onde.

$n_{s}=n_{0}$

${n}_{p}^{2}\quad =\quad {n}_{0}^{2}+{\frac {{\chi }_{xy}^{2}}{{n}_{0}^{2}}}\quad$

On a également les coefficients de réflexion suivant:

${r}_{pp}\quad =\quad {\frac {{n}_{0}(cos{\theta }_{0}-1)}{{n}_{0}(cos{\theta }_{0}+1)}}\left[1+{\frac {{\gamma }_{xy}.sin(2{\theta }_{0})}{{n}_{0}^{2}({n}_{0}^{2}cos{(2\theta }_{0})-1)}}\right]$

${r}_{ss}={\frac {cos{\theta }_{0}-{n}_{0}}{cos{\theta }_{0}+{n}_{0}}}$

Mise en place expérimentale sur couches minces ferromagnétiques

Il est possible de relier la variation de polarisation de l'onde électromagnétique avec l'aimantation du matériau :

$\alpha =\nu Md$ où α est l'angle de déviation, ν la constante de Verdet et d l'épaisseur du matériau.

Dans un matériau ferromagnétique en couche mince, l’aimantation s’aligne parallèlement au plan de la couche. Lorsqu’on le soumet à un champ magnétique extérieur, on peut modifier l’aimantation globale du matériau. Elle s'aligne avec le champ.

Remarque: Plus la couche est épaisse, plus il faudra un champ fort pour aligner l’aimantation.

Ce phénomène suit un cycle d’hystérésis particulier. En faisant varier le champ extérieur, on peut observer les variations de l’aimantation du matériau par effet Kerr.

Cycle d'hystérésis de l'aimantation sous champ magnétique

Pour des couches très minces, on peut utiliser les configurations polaire ou longitudinale pour observer cet effet. Cependant au-dessus d’une certaine épaisseur, la configuration polaire ne sera plus efficace car l’aimantation ne sera pas colinéaire à l’onde incidente. On peut y remédier en augmentant l’intensité du champ magnétique extérieur.

Si le matériau est composé de plusieurs couches minces, on peut également observer des cycles d’hystérésis imbriqués qui correspondent à chaque couche.

Les applications de l'effet Kerr magnéto-optique

Les phénomènes d'interactions entre la matière aimantée et la lumière (interactions magnéto-optiques) conduisent à une multitude d’applications dans des secteurs très divers comme le stockage des données, ou encore les télécommunications optiques. Plus précisément, deux phénomènes sont exploités dans la mise au point de technologies liées aux effets magnéto-optiques: l’effet Faraday, et l’effet Kerr magnéto-optique.

Cette section présente différentes applications et technologies impliquant l’effet Kerr magnéto-optique.

Applications de l’effet Kerr pour des dispositifs non réciproques

L’influence de la matière aimantée sur un faisceau de lumière traduit par l’effet Kerr en fait un outil très intéressant dans le traitement optique de l’information. Il est en effet possible de modifier la fréquence de l’onde lumineuse en utilisant un modulateur.

Pour cela, l’onde incidente est dirigée sur une couche mince de matériau ferromagnétique. Cette onde interagit avec la couche mince par effet Faraday et Kerr et est réfléchie par cette couche. L’onde réfléchie aura donc ses propriétés modifiées par l’un de ces deux effets.

L’effet Kerr modifie faiblement l’indice optique après réflexion sur une couche de matière aimantée, ce qui ne permet de faire qu’une faible modulation de la fréquence de l’onde incidente. Voilà pourquoi la plupart des modulateurs magnéto-optiques préfèrent l’effet Faraday à l’effet Kerr. Cependant, une configuration utilisant l’effet Kerr existe pour la modulation d’ondes hyperfréquences (quelques GHz) et permet d’atteindre une modulation plus efficace. Un champ hyperfréquence est appliqué à la fréquence de résonance de la couche aimantée qui réfléchit les ondes dans un guide d’ondes lentes.

Imagerie des domaines magnétiques

Principe de fonctionnement d'un microscope à effet Kerr

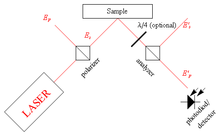
L’effet Kerr peut être utilisé pour cartographier les différents domaines magnétiques d’un matériau ferromagnétique. Il s’agit de la microscopie à effet Kerr. Cette microscopie a l’avantage d’être non destructrice et renseigne les domaines magnétiques et non les frontières magnétiques comme le fait la méthode de la poudre de Bitter. Ce type de microscopie a entre autres permis l’étude des parois des domaines magnétiques en régime dynamique. Elle est très utilisée dans l’étude des domaines magnétiques des matériaux en couches minces ou ultra-minces, par exemple les têtes de lectures magnétiques, notamment avec la technique de caractérisation SMOKE (Surface Magneto-Optic Kerr Effect).

Deux types de microscopies à effet Kerr existent : la méthode de la sonde optique et la méthode dite photographique. La première méthode utilise un faisceau polarisé, puis balayé sur la surface de l’échantillon et réfléchi, tandis que la deuxième éclaire la totalité de la surface de l’échantillon avec une lumière polarisée et capte les rayons réfléchis à l’aide d’un capteur CCD. Le principe de fonctionnement est sensiblement le même pour ces deux méthodes, la polarisation du rayon incident est modifiée par le champ magnétique généré par l’échantillon. Ce changement de polarisation est traduit par une variation de l’intensité du faisceau par un analyseur. Le faisceau est ensuite capté et transformé en image via un traitement d’image.

Têtes de lecture magnéto-optiques à effet Kerr

Les applications de l’effet Kerr concernent également le stockage de l’information. Un signal analogique ou numérique peut être enregistré sur une bande magnétique, soit une couche mince de matériaux ferromagnétiques, principalement du grenat, possédant une multitude de domaines magnétiques. L’orientation de ces domaines est utilisée pour stocker l’information. La bande magnétique peut ensuite être lue en utilisant l’effet Faraday ou l’effet Kerr. Pour cela, un faisceau polarisé est dirigé sur la bande magnétique. L’orientation des domaines magnétiques change l’état de polarisation du faisceau réfléchi, puis le signal électrique est récupéré via un analyseur.

Les dispositifs réalisant la lecture et l’enregistrement des données sont donc des transducteurs et sont appelées les têtes de lecture (d’écriture). Ces dernières peuvent être monopistes ou multipistes. Les têtes multiplistes permettent la lecture et l’enregistrement de pistes en parallèle, ce qui donne accès à un débit d’enregistrement et de lecture bien plus important.

La lecture par effet Faraday étant limitée en résolution par la longueur d’onde du faisceau incident et par la taille des grenats, le transducteur à effet Kerr a été mis au point. Avec ce type de transducteur, il est possible d’atteindre des densités de 1 μm²/bit sur des bandes magnétiques HI-8 ME. Il permet une meilleure densité d’informations sur la bande magnétique que son homologue à effet Faraday. Le transducteur possède plusieurs couches magnétiques sur lesquelles le faisceau est dirigé. Les couches magnétiques du transducteur sont appliquées sur la bande magnétique contenant l’information. Le champ magnétique de la bande oriente les domaines magnétiques des couches magnétiques du transducteur, sur lesquelles la lecture par effet Kerr longitudinal s’effectue.

Capteurs de courant à effet Kerr

Il est possible de mesurer l’intensité d’un courant électrique en utilisant l’effet Kerr. Pour cela, le déplacement d’un domaine magnétique sur une couche mince de permalloy est mesuré. Ainsi, lorsque le capteur est placé autour d’un fil de courant, le champ magnétique généré par celui-ci mettra en déplacement le domaine magnétique du permalloy.

Utilisation dans les mémoires magnéto-optiques.

Dans les mémoires magnéto-optiques, l’effet Faraday est souvent préféré à l’effet Kerr.

Pour ce type de mémoires non volatiles, l’information est stockée dans l’orientation des moments magnétiques d’un disque en matériau ferromagnétique. L’écriture des informations se fait en chauffant localement le disque à une température supérieure à la température de Curie par un faisceau laser. Ce faisceau a une puissance de l’ordre de la dizaine de milliwatt et est concentré sur une zone de 1 μm de diamètre. Ensuite, un champ magnétique est appliqué, ce qui a pour effet d’orienter le domaine magnétique de la matière chauffée. L’effet Kerr est utilisé pour la lecture des données à l’aide d’un faisceau de plus faible puissance (quelques milliwatts).

Bibliographie

• Umesh Tiwari, R. Ghosh, P. Sen, Theory of magneto-optic Kerr effects, School of Physical Sciences, Jawaharlal Nehru University, New Delhi, Inde.
• Mohammed Saib, Imagerie Magneto-optique du retournement de l’aimantation dans des couches minces de La 0,7 Sr 0,3 MnO 3 (Lire en ligne)

Voir aussi

Articles connexes

• Effet Faraday
• Optique non linéaire
• Effet électro-optique