Couplage de transformateurs triphasés
Les transformateurs de puissance font partie des composants clés des réseaux électriques en courant alternatif. Ceux-ci sont en pratique triphasés. Les enroulements des transformateurs, qu'ils se trouvent dans une même cuve dans le cas d'un transformateur triphasé ou répartis dans 3 transformateurs monophasés, peuvent être connectés de différentes manières entre eux et aux trois phases du réseau. Ces différentes connexions sont appelées couplage[1]. Les trois couplages possibles sont celui en étoile, en triangle et en zigzag. Le couplage du transformateur représente la combinaison du couplage du côté primaire, du côté secondaire voire du côté tertiaire. Un couplage de transformateur est exprimé en commençant par celui du primaire. Si le primaire est en étoile et le secondaire en triangle, cela donne donc un couplage étoile-triangle. Les couplages se différencient vis-à-vis de la tension et au courant qu'ont à supporter les enroulements, à la présence ou non d'un point de neutre et à leur impédance homopolaire. Cette dernière peut être choisie élevée afin de limiter les courants de court-circuit asymétrique ou bas afin de limiter la surtension dans les phases saines lors de défauts asymétrique. Une solution pour réduire l'impédance homopolaire est l'ajout d'un troisième enroulement connecté en triangle qui de plus symétrise les courants de court-circuit.
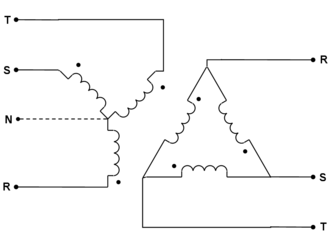
Description[modifier | modifier le code]
Connexion étoile[modifier | modifier le code]
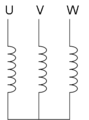
Dans la connexion étoile chaque enroulement de phase d'un transformateur triphasé est connecté à un point commun (point neutre) qui peut être mis ou non à la terre. L'autre extrémité étant reliée à la borne de ligne correspondante[2]. La tension aux bornes des bobines est la tension entre phases divisée par . Le courant traversant les bobines est le courant de ligne. Elle est représentée par la lettre Y.
-
Symbole d'un transformateur étoile-étoile
-
Schéma électrique de la connexion étoile
Connexion triangle[modifier | modifier le code]
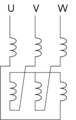
Dans la connexion triangle, la connexion des enroulements de phase d'un transformateur triphasé est effectuée de manière à réaliser un circuit fermé[3]. La tension aux bornes des bobines est la tension entre phases. Le courant traversant les bobines est le courant de ligne divisé par . Elle est représentée par la lettre D ou Δ. Il ne peut pas être mis à la terre.
-
Symbole d'un transformateur triangle-étoile
-
Schéma de la connexion triangle
Connexion zigzag[modifier | modifier le code]
Connexion des enroulements consistant en deux sections d'enroulement, la première section étant connectée en étoile et la seconde en série entre la première section et les bornes de ligne : les deux sections sont disposées de telle sorte que chaque phase de la deuxième section soit enroulée sur une colonne du transformateur différente de celle de la première section à laquelle elle est connectée[4]. Elle est représentée par la lettre Z. Elle combine certains des avantages des connexions étoiles et triangle. Ainsi, elle peut être mise à la terre de la même manière que les connexion étoiles.
-
Symbole d'un transformateur étoile-zigzag
-
Schéma de la connexion zigzag
Comme la connexion en triangle, la connexion zigzag supprime les harmoniques de rang 3[5]. Comme la connexion étoile, il offre un point de neutre et donc une impédance homopolaire non-infinie. Parmi ses défauts, il est relativement complexe à construire.
Symbole de couplage[modifier | modifier le code]
Le primaire du transformateur est connecté selon une connexion, tout comme le secondaire, la combinaison des deux est le couplage du transformateur. Le symbole de couplage indique les modes de connexions des enroulements et déphasages relatifs, exprimés par une combinaison de lettres et du ou des indices horaires. La majuscule représente la haute tension du transformateur. La minuscule représente la basse tension du transformateur. Le « n » représente le neutre sorti au secondaire (couplage étoile ou zig-zag)[6]. L'indice de couplage est complété par un « indice horaire » qui donne, par pas de 30°, le déphasage horaire en 12e de tour (comme sur une montre) entre le primaire et le secondaire du transformateur (exemple : 11 = 11×30° = 330° en sens horaire ou 30° en sens anti-horaire)[6].
Par exemple, un indice de couplage « Dyn11 » définit donc un transformateur dont :
- le système triphasé de tension élevé est en « triangle » ;
- le système triphasé de tension basse est en « étoile » avec neutre sorti (indiqué par le « n ») ;
- le décalage entre les deux systèmes est de 330° (= – 30° ou bien 11×30°).
Les couplages les plus utilisés en Allemagne sont : YNy0, Yzn5, YNd5, YNd11, Dyn5[7].
Comparatif[modifier | modifier le code]
La connexion étoile a les avantages suivants[8] :
- plus économique pour les transformateurs de haute tension
- a un point de neutre disponible
- permet la mise à la terre directe ou la mise à la terre à travers une impédance
- permet de réduire le niveau d'isolation du neutre (isolation graduée)
- permet de loger les prises d'enroulement et les changeurs de prises à l'extrémité neutre de chaque phase
La connexion triangle a les avantages suivants[9],[10]:
- plus économique pour un enroulement à courant fort et à basse tension
- combiné avec un enroulement à couplage étoile, réduit l'impédance homopolaire dans cet enroulement
- si la connexion est réalisée à l'aide de transformateur monophasé, en cas de perte d'une unité, les deux autres phases peuvent continuer à transmettre de la puissance.
Et les désavantages suivants :
- absence de neutre
- en cas de surtension transitoire, l'absence de neutre fait que les tensions dans les différents enroulements ne sont pas égales. La tension phase neutre peut devenir particulièrement élevé. Il faut donc augmenter les distances d'isolement en conséquence, ce qui entraîne un surcoût. Pour ces raisons, les enroulements triangle sont généralement limités à des systèmes ayant une tension maximale phase à -phase inférieure à 345 kV.
La connexion en zigzag a les avantages suivants[11] :
- Peut recevoir une charge de courant de neutre avec une basse impédance homopolaire inhérente
- réduit le déséquilibre de tension dans les réseaux où la charge n'est pas répartie également entre les phases.
Utilisations[modifier | modifier le code]
Les avantages et les défauts des différents couplages conditionnent leurs utilisations.
- Pour les grands transformateurs dans le réseau très haute tension le couplage YNyn0 ou YNyd5 est souvent utilisé pour limiter le besoin en isolation des transformateurs à cause de la haute tension d'une part et fournir une mise à la terre de faible impédance d'autre part[12],[13].
- Pour les transformateurs reliant le réseau très haute tension à la moyenne tension, un couplage Yy0 est adapté pour les mêmes raisons que précédemment. De plus les réseaux haute tension ne présentent normalement peu de dissymétrie : il n'est pas nécessaire de les compenser avec un enroulement triangle[13].
- Le couplage Yz5 est utilisé pour les transformateurs de distribution électrique d'une puissance inférieure à 250 kVA[12]. Les propriétés de rééquilibrage de la tension sont en effet très utile dans un réseau de distribution où les charges ne sont pas forcément également réparties entre les différentes phases (les particuliers sont connectés en monophasé). Le couplage Dy5 est utilisé pour les transformateurs de distribution électrique d'une puissance supérieure à 250 kVA[12]. L'économie de cuivre par rapport au couplage Yz5 devient alors intéressante, un Dz5 serait difficile pour les petites puissantes car le diamètre du câble des enroulements deviendrait trop faible[14].
- Pour les transformateurs associés à des moteurs un couplage Yd5 est privilégié, tout comme pour la connexion des générateurs électriques des centrales électriques : du côté où le courant est fort on connecte en delta pour le réduire, côté haute-tension on connecte en étoile pour la réduire[12],[15].
- Les transformateurs alimentant le réseau auxiliaire d'une centrale électrique peuvent être connectés en étoile-étoile, étoile-triangle ou triangle-triangle. Ce dernier est privilégié pour les grandes puissances. La faible taille de ce type de réseau n'impose pas de mettre à la terre les transformateurs[13].
Impédance homopolaire[modifier | modifier le code]
Introduction[modifier | modifier le code]
Transformation de Fortescue[modifier | modifier le code]
La transformation de Fortescue est utilisée afin de simplifier l'analyse des systèmes électriques triphasées déséquilibrés. Elle décompose un système triphasée en:
- un système équilibré direct dont les grandeurs sont notées d'un indice d ;
- un système équilibré inverse dont les grandeurs sont notées d'un indice i ;
- un système de tension homopolaire dont les grandeurs sont notées d'un indice 0
La composante homopolaire de la tension et du courant d'un système triphasé (a, b et c) se calcule grâce à la matrice de Fortescue[16]:
Où a est un nombre complexe de module 1 et d'argument : . Ainsi pour un système équilibré:
La transformation de Fortescue est principalement utilisée pour le calcul des courants de court-circuit.
Courant de court-circuit[modifier | modifier le code]
En cas de court-circuit asymétrique, la connaissance de l'impédance homopolaire du système est indispensable pour la détermination de la valeur du courant. Ainsi en cas de défaut monophasé, le courant vaut , où Un est la tension nominale du réseau, est un facteur de tension selon les tolérances acceptées sur la valeur de la tension, Zd est l'impédance directe du système, Zi celle indirecte et Z0 celle homopolaire[16].
Le sens de rotation du champ magnétique n'ayant pas d'incidence sur le comportement d'un transformateur, leur impédance directe et indirecte sont égales : Zd=Zi.
L'impédance homopolaire d'un transformateur électrique dépend de son couplage et son circuit magnétique[17]. Une impédance homopolaire élevée permet de limiter le courant de court-circuit, cependant cela provoque de fortes surtensions sur les phases saines lors des défauts asymétriques.
Impédance homopolaire des transformateurs à deux enroulements[modifier | modifier le code]
Modèle en T[modifier | modifier le code]

L'impédance directe d'un transformateur à deux enroulements peut-être modélisée grâce à un modèle en T comme présenté ci-contre. est l'impédance principale, aussi appelée impédance de magnétisation. Les grandeurs liées au primaire sont notées d'un I et celles liées au secondaire d'un II. Une autre convention répandue est de noter les grandeurs du primaire d'un 1 ou d'un p et celles du secondaire d'un 2 respectivement d'un s[18]. L'impédance de court-circuit, ou de fuite, entre les deux enroulements notée est divisée en deux parties pour le primaire et pour le secondaire. Ramené au primaire, si l'impédance de court-circuit en pour cent est notée en minuscule , on a[19] :
Où est la tension assignée de l'enroulement primaire et est la puissance apparente du transformateur.
L'impédance principale est de plusieurs ordres de grandeurs plus grande que l'impédance de court-circuit.
Comme déjà indiqué pour un transformateur Zd=Zi. Cela signifie que et . De manière générale, Zd n'est pas égale à Z0[20]. Cependant, l'impédance homopolaire de court-circuit entre les deux enroulements principaux ne diffère normalement que légèrement de l'impédance directe. Cette différence est de l'ordre de 10 % à 20 %, en fonction de la position des enroulements. Cependant, si des inductances supplémentaires sont connectées dans une connexion en triangle, son impédance homopolaire deviendra beaucoup plus grande[21].
Cas des connexions non reliées à la terre[modifier | modifier le code]
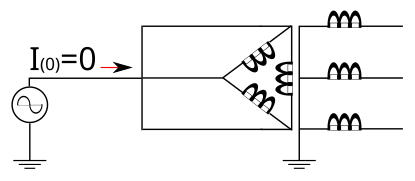
Un courant homopolaire ne peut entrer, ou sortir, dans une connexion en triangle, ainsi que celle en étoile et zigzag dont le neutre n'est pas mis à la terre. En effet, le courant entrant dans un système doit en ressortir. Or, les trois seuls courants présents sont ceux des trois phases. On a donc automatiquement ;. L'impédance homopolaire vue depuis le côté du transformateur non relié à la terre est infinie dans ce cas. On modélise ce cas par un circuit ouvert.
-
Le courant homopolaire ne peut entrer dans un enroulement connecté en étoile non mis à la terre
-
Le courant homopolaire ne peut entrer dans un enroulement connecté en triangle
-
Le courant homopolaire peut être induit dans un enroulement connecté en triangle mais n'en sort alors pas
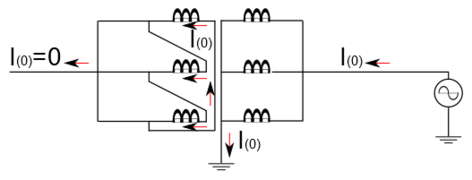
Les courants homopolaires peuvent toutefois être induits dans une connexion en triangle. La tension entre phases traversant un enroulement en triangle conduit automatiquement à une somme égale à zéro en raison du couplage en triangle fermé. Un enroulement en triangle représente donc un court-circuit pour la composante homopolaire[22], seules les impédances de court-circuit sont donc à prendre en compte pour le calcul de l'impédance homopolaire. Ils tournent alors dans les enroulements sans affecter le réseau. Le flux homopolaire qu'il induit dans le noyau compense celui provenant des autres enroulements[23].
-
Une connexion triangle est court-circuitée pour les courants homopolaires
-
Des bobines non couplées magnétiquement aux autres enroulements peuvent être installées dans le triangle afin de limiter le courant homopolaire la traversant
Impédance principale homopolaire[modifier | modifier le code]

L'impédance principale, aussi appelée de magnétisation, d'un transformateur est grande comparativement à l'impédance de court-circuit. Dans les systèmes directs et indirects, on peut, dans la plupart des cas, négliger le courant de magnétisation qui la traverse. Ce n'est pas le cas dans le système homopolaire où par exemple pour les transformateurs YNy elle présente le seul chemin possible pour les courants[24]. Pour un transformateur triphasé à deux enroulements, l'impédance principale homopolaire dépend de la construction du noyau magnétique :
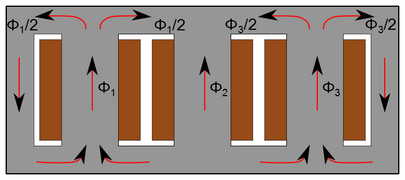
- Dans le cas de noyau disposant de colonnes non bobinées, la reluctance au flux homopolaire est faible : le flux reste confiné dans le noyau. En effet, celui-ci peut circuler dans ces colonnes sans obstacle. Dans le cas des couplages étoile-étoile, cela a pour effet de saturer le circuit magnétique comme aucun enroulement ne vient compenser le flux homopolaire. Ce flux homopolaire induit également une tension homopolaire importante[25]. Pour un couplage étoile-étoile, où aucun chemin alternatif n'est fourni au courant homopolaire (voir ci-contre), l'impédance homopolaire est alors quasiment égale à l'impédance principale . Celle-ci étant beaucoup plus grande que l'impédance de court-circuit, le ratio est compris entre 10 et 100[18].
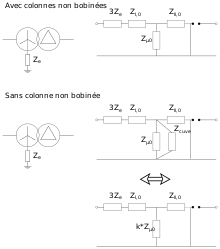
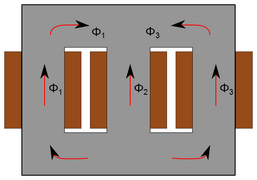
- Si le noyau n'a pas de colonne non bobinée, la somme des flux dans les culasses est nulle. En d'autres mots, un flux homopolaire ne peut circuler dans le noyau. Il ne peut circuler que par la cuve du transformateur. L'intervalle entre le noyau magnétique et la cuve joue le rôle d'entrefer, la reluctance au flux homopolaire est grande, son inductance est donc faible[26],[24]. L'avantage par rapport à un noyau avec colonnes non bobinées est que le circuit magnétique ne sature pas en cas de présence de courant homopolaire[27]. Une valeur d'environ 10 % le courant nominal est acceptable pour le transformateur. Il n'y a pas non plus de tension homopolaire induite[25]. Le défaut est que les parois de la cuve s'échauffe sous l'effet des courants de Foucault[28]. Ceux-ci induisent à leur tour un flux dans le noyau. Conformément à la loi de Lenz, le flux total dans le noyau s'en trouve réduit. Sur le plan de la modélisation, le chemin offert par la cuve aux flux homopolaire est représenté par une inductance mise en parallèle de l'inductance principale du transformateur. On peut regrouper les deux inductances en remplaçant l'impédance principale par avec k plus petit que un. L'impédance homopolaire d'un transformateur sans colonne non bobinée est donc inférieure à celle d'un transformateur en étant équipé[27],[24]. Pour un couplage étoile-étoile, où aucun chemin alternatif n'est fourni au courant homopolaire, la fraction est comprise typiquement entre 3 et 10[29].
- Les transformateurs monophasés connectés en banc ont toujours des colonnes non bobinées afin de permettre au flux de circuler. Ils sont donc équivalents aux transformateurs triphasés avec colonnes non bobinées[18].
-
Répartition du flux dans un noyau avec deux colonnes pour le retour du flux lorsque les trois phases sont équilibrées. Le fait que le flux des différentes phases se divise en deux permet de réduire de moitié la section des culasses
-
Répartition du flux dans un noyau avec deux colonnes pour le retour du flux lorsque la phase 1 a plus de tension et donc plus de flux
-
Répartition du flux dans un noyau sans colonne non bobinée lorsque les trois phases sont équilibrées
-
Répartition du flux dans un noyau sans colonne pour le retour du flux lorsque la phase 1 a plus de tension et donc plus de flux. Le flux homopolaire ne pouvant circuler dans le noyau, il cherche une voie de retour à travers la cuve du transformateur. L'espace entre le noyau et la cuve joue le rôle d'entrefer.
Modélisation de l'impédance homopolaire pour différents couplages[modifier | modifier le code]
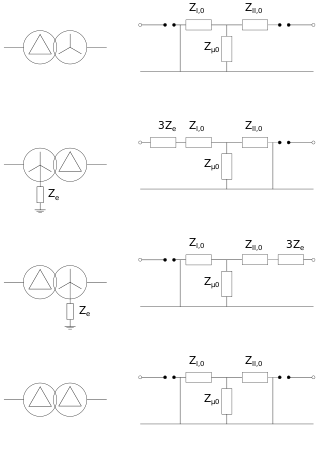
L'impédance homopolaire des transformateurs à deux enroulements peut être modélisée comme suit selon le couplage[30],[31]:
-
Schéma de l'impédance homopolaire de transformateur étoile-étoile en fonction de leur mise à la terre.
-
Schéma de l'impédance homopolaire de transformateur étoile-triangle en fonction de leur mise à la terre.
-
Schéma de l'impédance homopolaire de transformateur étoile-zigzag en fonction de leur mise à la terre (incomplet)
Impédance homopolaire des transformateurs à trois enroulements[modifier | modifier le code]
Idée[modifier | modifier le code]
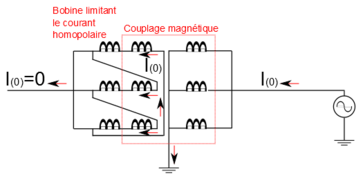
Un troisième enroulement connecté en triangle afin d'offrir un chemin au courant homopolaire peut être ajouté à un transformateur. Il sert dans le cas de transformateur YNyn à réduire l'impédance homopolaire du système connecté (utile seulement en cas de dissymétrie, en cas de défaut par exemple) et par la même occasion le facteur de défaut à la terre[32]. En contre-partie le courant de court-circuit augmente lors de défauts dissymétrique. Si cet enroulement n'est relié à aucune phase, on parle d'enroulement de stabilisation. On peut toutefois l'utiliser pour alimenter des charges basses tensions[33]. On note la présence d'un enroulement de stabilisation par « +d » dans le symbole de couplage[15].
Les enroulements de stabilisation doivent être dimensionnés afin de pouvoir supporter les courants de court-circuit pouvant survenir dans les réseaux connectés. La connexion de bobines d'inductance intégrées dans le triangle (voir Cas des connexions non reliées à la terre) permet de diminuer le courant de défaut induit à une valeur acceptable[34]. Traditionnellement la puissance nominale de l'enroulement de stabilisation est choisie égale à un tiers de celle des enroulements principaux[33].
Modèle en T[modifier | modifier le code]

L'impédance directe d'un transformateur à trois enroulements peut être modélisé grâce à un modèle en T comme présenté ci-contre. Comme pour un transformateur à deux enroulements, est l'impédance principale, aussi appelée impédance de magnétisation. Il n'y a plus une mais trois impédances de court-circuit distinctes : entre le primaire et le secondaire notée , entre le primaire et le tertiaire notée et entre secondaire et le tertiaire notée . Elles peuvent être exprimées en pourcentage de l'impédance du transformateur. Pour en déduire les valeurs de , et , on peut poser le système d'équations suivant :
- .
On en déduit[21] :
- .
En fait le troisième enroulement est généralement négligé dans le calcul des impédances directes et indirectes, le courant le parcourant étant faible. Il est par contre pris en compte pour le calcul de l'impédance homopolaire[35].
Modélisation de l'impédance homopolaire pour le couplage Yyd[modifier | modifier le code]

Dans le cas d'un couplage étoile-étoile avec mise à la terre au primaire, l'impédance homopolaire de l'enroulement de stabilisation est en parallèle de l'impédance principale du transformateur. La première étant nettement plus petite que la seconde, l'impédance homopolaire de l'ensemble est significativement réduite.
Tableau récapitulatif[modifier | modifier le code]
Le rapport de l'impédance homopolaire Z0 sur l'impédance directe Zd est donné dans le tableau suivant pour diverses configurations[15],[36],[29] :
| Type de Noyau magnétique | Couplage | |||
|---|---|---|---|---|
| Yzn5 | YNd ou Dny | YNy | YNy+d | |
| À 3 colonnes bobinées | 0,1-0,15 | 0,7 - 1 | 3 - 10 | 1 - 2,4 |
| À 3 colonnes bobinées et 2 colonnes non bobinées | 0,1-0,15 | 1 | 10 - 100 | 1 - 2,4 |
| 3 transformateurs monophasés | 0,1-0,15 | 1 | 10 - 100 | 1 - 2,4 |
3e harmonique[modifier | modifier le code]
Les connexions mises à la terre laissent passer le courant de 3e harmonique (150 Hz). En effet, pour les harmoniques de rang 3 la somme des courants venant des trois phases ne s'annule pas : ce sont en fait des courants homopolaires. Les remarques faites à propos de ce dernier s'appliquent donc au courant de 3e harmonique. Par exemple, il ne peut entrer dans des connexions en triangle.
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (de) Eckhard Spring, Elektrische Maschinen, Berlin, Heidelberg, New York, Springer, (ISBN 3-540-28241-6)
- (de) D. Oeding et B.R. Oswald, Elektrische Kraftwerke und Netze, Berlin, Springer, (lire en ligne), p. 217-255
- (en) James H. Harlow, Electric power transformer engineering, CRC Press, , p. 128-160
- Analyse des réseaux triphasés en régime perturbé à l’aide des composantes symétriques, (lire en ligne)
- (en) Karim Shaarbaf, Transformer Modelling Guide, Teshmont, (lire en ligne)
- (de) B.R. Oswald, Vorlesung Elektrische Energieversorgung I, Skript Transformatoren, Université de Hanovre, (lire en ligne)
Références[modifier | modifier le code]
- Vector group en anglais et Schaltgruppe en allemand
- CEI 60076-1, clause 3.10.1, version 2011
- CEI 60076-1, clause 3.10.2, version 2011
- CEI 60076-1, clause 3.10.4, version 2011
- (en) P.P. Khera, « Application of zigzag transformers for reducing harmonics in the neutral conductor of low voltage distribution system », IEEE Trans. on Industry Applications, (DOI 10.1109/IAS.1990.152320, lire en ligne)
- Oeding, p. 217-255
- Oswald 2005, p. 18
- CEI 60076-8, clause 2.1.1, version 1997
- CEI 60076-8, clause 2.1.2, version 1997
- Harlow 2004, p. 307
- CEI 60076-8, clause 2.1.3, version 1997
- Spring 2006, p. 187
- Oswald 2005, p. 40
- (de) Josef Kindersberger, Energieübertragungstechnik, TU Munich, , p. 51
- Oeding 2004, p. 223
- Analyse des réseaux triphasés en régime perturbé à l’aide des composantes symétriques, Schneider electric, (lire en ligne)
- Kindersberger 2010, p. 52
- Oswald 2005, p. 26
- CEI 60076-8, cl. 4.2 et 5.2, version 1997
- CEI 60076-8, cl. 4.2, version 1997
- CEI 60076-8, cl. 5.3, version 1997
- CEI 60076-8, cl. 4.5, version 1997
- Kindersberger 2010, p. 56
- Oswald 2005, p. 27
- Oswald 2005, p. 31
- Shaarbaf 2014, p. 50
- Kindersberger 2010, p. 54
- Harlow 2004, p. 305
- Oswald 2005, p. 56
- Shaarbaf 2014, p. 51-53
- Oswald 2005, p. 43
- CEI 60076-8, clause 4.7.2, version 1997
- Kindersberger 2010, p. 58
- CEI 60076-8, cl. 4.7.2, version 1997
- Oswald 2005, p. 34
- CEI 60076-8, cl. 4.7, version 1997