Cercles d'Apollonius (fractale)
En mathématiques, la figure des cercles d'Apollonius est un empilement compact de cercles dans un cercle. Elle est construite en itérant la construction d'Apollonius des deux cercles tangents à trois cercles deux à deux tangents. Sa densité est égale à 1, ce qui signifie que l'aire laissée par les interstices est nulle. C'est aussi une figure de géométrie fractale dont on a calculé la dimension.
Elle a été ainsi nommée en l'honneur du mathématicien grec Apollonius de Perge qui a posé le problème de la détermination des cercles tangents à trois cercles.
La partie centrale de la figure située entre les trois cercles initiaux, que l'on retrouve une infinité de fois dans la figure, s'appelle une baderne d'Apollonius [1],[2],[3].
-
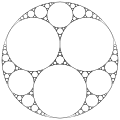
Figure des cercles d'Apollonius, partant de trois cercles de même taille.
-
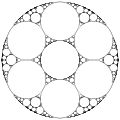
Baderne d'Apollonius, empilement de cercles situés entre trois cercles extérieurement tangents de même taille, formée elle-même de trois badernes, elles-mêmes formées...
Origine de l'appellation "baderne"
[modifier | modifier le code]D'après François Apéry[4] qui cite Benoit Mandelbrot, ce dernier a créé le terme anglais "apollonian gasket" (joint de culasse apollonien) en 1977, en même temps que le terme "Sierpinski gaskett" (tamis de Sierpinki, fractale de construction similaire) en pensant aux "feuilles de caoutchouc trouées assurant l'étanchéité des moteurs". La traduction française "baderne d'Apollonius" serait due à Bouvier et George dans la première édition de leur dictionnaire de mathématiques en 1979[2], le mot "gaskett" désignant aussi une corde marine. Mandelbrot aurait préféré le terme "garcette".
Construction
[modifier | modifier le code]La figure des cercles d'Apollonius peut être construite comme suit. On débute avec trois cercles C1, C2 et C3, chacun d'eux étant tangent aux deux autres (dans la construction générale, ces trois cercles peuvent avoir n'importe quelle taille, tant qu'ils sont tangents). Apollonius découvrit qu'il existe deux autres cercles qui n'ont pas d'intersection, C4 et C5, qui ont la propriété d'être tangents avec les trois cercles originaux — ceux-ci ont été appelés cercles d'Apollonius.
En ajoutant les deux cercles d'Apollonius aux trois cercles originaux, nous avons maintenant cinq cercles.
Prenons un des deux cercles d'Apollonius - disons C4. Il est tangent à C1 et C2, donc le triplet de cercles C4, C1 et C2 ont leur propres cercles d'Apollonius. Nous connaissons déjà un de ceux-ci - c'est C3 - mais l'autre est un nouveau cercle C6.
D'une manière similaire, nous pouvons construire un nouveau cercle C7 qui est tangent à C4, C2 et C3, et un autre cercle C8 à partir de C4, C3 et C1. Ceci nous donne 3 nouveaux cercles. Nous pouvons construire trois autres nouveaux cercles à partir de C5, donnant six nouveaux cercles. En prenant les cercles de C1 jusqu'à C5, ceci donne un total de 11 cercles.
En continuant la construction étape par étape de cette manière, nous pouvons ajouter 2×3n nouveaux cercles à l'étape n, donnant un total de 3n+1+2 cercles après n étapes.
Il n'a été démontré qu'en 1943 que l'ensemble résiduel, complémentaire des disques dans le grand disque, a une aire nulle [5],[6], donc que l'empilement est complet, et seulement en 1973 qu'il possède une dimension de Hausdorff égale environ à 1,3057 [7] ; voir la suite A052483 de l'OEIS.
Variations
[modifier | modifier le code]
Les cercles d'Apollonius peuvent aussi être construits en remplaçant un des cercles générateurs par une droite, qui peut être vue comme un cercle passant par le point à l'infini.
Deux des cercles générateurs peuvent aussi être remplacés par des droites parallèles, qui peuvent être vues comme étant tangentes à l'infini. Dans cette construction, les cercles qui sont tangents à une des deux droites forment une famille de cercles de Ford.
L'extension de la figure des cercles d'Apollonius à la dimension trois est baptisée « figure des sphères d'Apollonius ». Sa dimension fractale a été estimée à 2,47[8] ; voir la suite A187089 de l'OEIS.
Symétries
[modifier | modifier le code]Si les trois cercles originaux ont le même rayon, alors la figure des cercles d'Apollonius possède trois axes de symétrie ; ces droites sont mutuellement tangentes à chaque paire de cercles. Chaque tangente mutuelle passe aussi par le centre du troisième cercle et le centre commun du premier des deux cercles d'Apollonius. Ces axes de symétrie forment des angles de 60 degrés, donc la construction des cercles d'Apollonius a aussi une symétrie rotationnelle d'ordre 3. Plus généralement, partant d'une famille de n cercles de même rayon tangents deux à deux, on obtient une famille de cercles d'Apollonius ayant une symétrie rotationnelle d'ordre n, comme on le voit ci-dessous.
Courbures entières
[modifier | modifier le code]Les courbures (les inverses des rayons) d'un ensemble de quatre cercles tangents trois à trois sont liées par la relation de Descartes : Si on désigne alors par et les courbures des deux cercles tangents aux trois premiers, on obtient ; on en déduit de proche en proche que si quatre des courbures d'un ensemble de cercles d'Apollonius sont entières, elles le sont toutes[9].
Liens avec la géométrie hyperbolique
[modifier | modifier le code]Les trois cercles générateurs, et par conséquent la construction entière, sont déterminés par la localisation des trois points de contact. Puisqu'il existe une transformation de Möbius qui applique trois points donnés quelconques dans le plan à trois autres points quelconques, et puisque les transformations de Möbius respectent les cercles, il existe une transformation de Möbius qui applique deux familles de cercles d'Apollonius quelconques à une troisième.
Les transformations de Möbius sont aussi des isométries du plan hyperbolique, donc dans la géométrie hyperbolique, toutes les constructions de cercles d'Apollonius sont isométriques. Dans un sens, il n'existe par conséquent qu'une famille de cercles d'Apollonius, qui peut être pensée comme un pavage du plan hyperbolique par des cercles et des triangles hyperboliques.
La réunion des cercles d'Apollonius est l'ensemble limite (ou attracteur) d'un groupe de transformations de Möbius connu sous le nom de groupe kleinéen.
Notes et références
[modifier | modifier le code]Notes
[modifier | modifier le code]- François Apéry, La Baderne d'Apollonius, Strasbourg, Université Louis Pasteur, Institut de Recherche Mathématique Avancée, (lire en ligne)
- Alain Bouvier, Michel Georges, François Le Lionnais, Dictionnaire des mathématiques, 2005, PUF, p. 47
- « Baderne d'Apollonius », sur MATHCURVE.COM (consulté le ).
- François Apéry, « A propos de l'article intitulé "La baderne d'Apollonius" », La gazette des mathématiciens,
- (en) EDWARD KASNER, FRED SUPNICK, « THE APOLLONIAN PACKING OF CIRCLES », Department of mathematics, Columbia University, (lire en ligne)
- François Apéry, « La baderne d'Apollonius », La gazette des mathématiciens, no 19, , p. 59-61 (lire en ligne
 )
)
- (en) Curtis T. McMullen, Hausdorff dimension and conformal dynamics III: Computation of dimension.
- (en) M. Borkovec, W. De Paris et R. Peikert, The Fractal Dimension of the Apollonian Sphere Packing [PDF].
- (en) Ronald Graham, Jeffrey Lagarias, Colin Mallows, Allan Wilks et Catherine Yan, Apollonian Circle Packings: Number Theory, J. Number Theory 100 (2003), 1--45
Références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Apollonian gasket » (voir la liste des auteurs).
- (en) Alexander Bogomolny, Apollonian Gasket, Cut-the-Knot
- (en) Benoît Mandelbrot, The Fractal Geometry of Nature, W H Freeman, 1982 (ISBN 0-7167-1186-9)
- (en) Paul D. Bourke : "An Introduction to the Apollony Fractal". Computers and Graphics, Vol 30, Issue 1, January 2006, pages 134-136.
- (en) David Mumford, Caroline Series, David Wright: Indra's Pearls: The Vision of Felix Klein, Cambridge University Press, 2002 (ISBN 0-521-35253-3)
Voir aussi
[modifier | modifier le code]Article connexe
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- How to compute and draw Apollonian gasket sur wikibooks
- Circle Inversion Fractals, fractales obtenues comme attracteurs d'une famille d'inversions