Auto-encodeur

Un auto-encodeur (autoencodeur), ou auto-associateur^[1]^,^[2]^:19 est un réseau de neurones artificiels utilisé pour l'apprentissage non supervisé de caractéristiques discriminantes^[3]^,^[4]. L'objectif d'un auto-encodeur est d'apprendre une représentation (encodage) d'un ensemble de données, généralement dans le but de réduire la dimension de cet ensemble. Récemment^[Quand ?], le concept d'auto-encodeur est devenu plus largement utilisé pour l'apprentissage de modèles génératifs^[5]^,^[6].

Historique[modifier | modifier le code]

L'auto-encodeur a d'abord été proposé comme une généralisation non linéaire de l'analyse en composantes principales (ACP) par Kramer^[7]. L'auto-encodeur a également été appelé l'auto-associateur^[7], ou réseau Diabolo^[8]. Ses premières applications datent du début des années 1990^[9]^,^[10]. Leur application la plus traditionnelle était réduction de la dimensionnalité ou apprentissage de représentations, mais le concept est devenu largement utilisé pour apprentissage de modèle génératifs de données^[11]^,^[12]. Certaines des IA les plus puissantes des années 2010 impliquaient des auto-encodeurs empilés à l'intérieur de réseaux de neurones profond^[13].

Architecture[modifier | modifier le code]

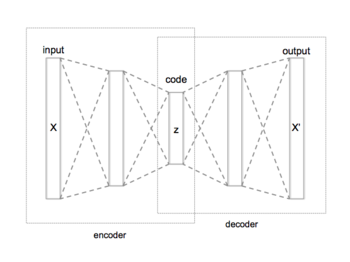
La forme la plus simple d'un auto-encodeur est un réseau de neurones non récurrents qui se propage vers l'avant, très semblable au perceptron multicouches. L'auto-encodeur a une couche d'entrée $X$ , une couche de sortie $X'$ ainsi qu'une ou plusieurs couches cachées les reliant. Toutefois la couche de sortie possède le même nombre de nœuds que la couche d'entrée ; autrement dit $X$ et $X'$ ont le même nombre de dimensions. Le code $\mathbf {z}$ (aussi appelé variables latentes ou représentation latente) est la couche cachée la plus interne. Elle représente $X$ mais dans un espace avec moins de dimensions.

L'objectif de l'auto-encodeur est de reconstruire ses entrées : prédire une valeur cible $X'$ la plus proche des entrées $X$ (plutôt que de prédire une valeur cible $Y$ étant donné les entrées $X$ ). Par conséquent, un auto-encodeur est un modèle d'apprentissage non supervisé.

Formalisation générale[modifier | modifier le code]

Plus formellement, un auto-encodeur se compose toujours de deux parties, l'encodeur et le décodeur, qui peuvent être définies comme des transitions $\phi$ et $\psi$ , telles que :

\phi :{\mathcal {X}}\rightarrow {\mathcal {F}}

\psi :{\mathcal {F}}\rightarrow {\mathcal {X}}

\phi ,\psi =\arg \min _{\phi ,\psi }\|X-(\psi \circ \phi )X\|^{2}

où ${\mathcal {X}}=\mathbb {R} ^{d}$ est l'espace où sont $X$ et $X'$ , et où ${\mathcal {F}}=\mathbb {R} ^{p}$ est l'espace où est le code $\mathbf {z}$ .

Généralement, l'espace caractéristique ${\mathcal {F}}$ possède une dimension inférieure à celui de l'espace d'entrée ${\mathcal {X}}$ . Ainsi le vecteur caractéristique $\phi (x)$ peut être considéré comme une représentation compressée de $x$ . Si les couches cachées possèdent une taille plus grande que celle de la couche d'entrée, l'auto-encodeur peut potentiellement apprendre la fonction identité et devenir sans intérêt. Toutefois, des résultats expérimentaux ont montré que dans ce genre de cas, l'auto-encodeur pouvait malgré tout apprendre des caractéristiques utiles^[2]^:19.

Architecture avec une seule couche cachée[modifier | modifier le code]

Décrivons l'architecture lorsqu'il n'y a qu'une seule couche cachée. L'étape d'encodage prend l'entrée $\mathbf {x} \in {\mathcal {X}}$ et l'associe au code $\mathbf {z} \in {\mathcal {F}}$ par la relation :

\mathbf {z} =\sigma (\mathbf {Wx} +\mathbf {b} )

où $\sigma$ est une fonction d'activation, (e.g. la sigmoïde ou la fonction ReLU), $\mathbf {W}$ une matrice de poids et $\mathbf {b}$ un vecteur de biais.

Ensuite, l'étape de décodage associe $\mathbf {z}$ à la reconstruction $\mathbf {x'}$ de forme identique à $\mathbf {x}$ :

\mathbf {x'} =\sigma '(\mathbf {W'z} +\mathbf {b'} )

où les $\mathbf {\sigma '} ,\mathbf {W'} ,{\text{ et }}\mathbf {b'}$ du décodeur peuvent différer ou non des $\mathbf {\sigma } ,\mathbf {W} ,{\text{ et }}\mathbf {b}$ de l'encodeur, selon la conception de l'auto-encodeur.

Un auto-encodeur est aussi entrainé pour minimiser l'erreur de reconstruction, e.g., erreur quadratique :

{\mathcal {L}}(\mathbf {x} ,\mathbf {x'} )=\|\mathbf {x} -\mathbf {x'} \|^{2}=\|\mathbf {x} -\sigma '(\mathbf {W'} (\sigma (\mathbf {Wx} +\mathbf {b} ))+\mathbf {b'} )\|^{2}

où $\mathbf {x}$ est généralement la moyenne d'un ensemble de données d'apprentissage.

Variations[modifier | modifier le code]

Différentes techniques existent pour empêcher un auto-encodeur d'apprendre la fonction identité et améliorer sa capacité à apprendre des représentations plus riches :

Auto-encodeur débruiteur[modifier | modifier le code]

Un auto-encodeur débruiteur prend une entrée partiellement corrompue et apprend à récupérer l'entrée originale débruitée. Cette technique a été introduite avec une approche spécifique d'une bonne représentation^[14]. Une bonne représentation est celle qui peut être obtenue de manière robuste à partir d'une entrée corrompue et qui sera utile pour récupérer l'entrée débruitée correspondante. Cette définition contient les hypothèses implicites suivantes :

Les représentations de haut-niveau sont relativement stables et robustes à la corruption de l'entrée;
Il est nécessaire d'extraire des caractéristiques qui soient utiles pour la représentation de la distribution d'entrée.

Pour entrainer un auto-encodeur à débruiter des données, il est nécessaire d'effectuer un mappage stochastique préliminaire $\mathbf {x} \rightarrow \mathbf {\tilde {x}}$ afin de corrompre les données et d'utiliser $\mathbf {\tilde {x}}$ comme entrée d'un auto-encodeur classique, avec comme seule exception de calculer la perte pour l'entrée initiale ${\mathcal {L}}(\mathbf {x} ,\mathbf {{\tilde {x}}'} )$ au lieu de ${\mathcal {L}}(\mathbf {\tilde {x}} ,\mathbf {{\tilde {x}}'} )$ .

Auto-encodeur épars[modifier | modifier le code]

En imposant la parcimonie sur les unités cachées durant l'apprentissage (tout en ayant un plus grand nombre d'unités cachées que d'entrées), un auto-encodeur peut apprendre des structures utiles dans les données d'entrées. Cela permet de représenter de façon éparse les entrées, ces représentations pouvant être utilisées pour le pré-entrainement de tâches de classification.

La parcimonie peut être obtenue en ajoutant des termes additionnels à la fonction objectif durant l'apprentissage (en comparant la distribution de probabilité des couches cachées avec une valeur faible désirée)^[15], ou en réduisant manuellement à 0 toutes sauf les quelques activations d'unités cachées les plus fortes (appelé auto-encodeur k-épars)^[16].

Auto-encodeur variationnel[modifier | modifier le code]

Le modèle d'auto-encodeur variationnel hérite de l'architecture de l'auto-encodeur, mais fait des hypothèses fortes concernant la distribution des variables latentes. Il utilise l'approche variationnelle pour l'apprentissage de la représentation latente, ce qui se traduit par une composante de perte additionnelle et un algorithme d'apprentissage spécifique fondé sur un estimateur bayésien variationnel du gradient stochastique^[5]. Il suppose que les données sont produites par un modèle graphique orienté $p(\mathbf {x} |\mathbf {z} )$ et que l'encodeur apprend une approximation $q_{\phi }(\mathbf {z} |\mathbf {x} )$ de la distribution a posteriori $p_{\theta }(\mathbf {x} |\mathbf {z} )$ où $\mathbf {\phi }$ et $\mathbf {\theta }$ désignent respectivement les paramètres de l'encodeur (modèle de reconnaissance) et du décodeur (modèle génératif). L'objectif de l'auto-encodeur, dans ce cas ci, a la forme suivante :

{\mathcal {L}}(\mathbf {\phi } ,\mathbf {\theta } ,\mathbf {x} )=D_{KL}(q_{\phi }(\mathbf {z} |\mathbf {x} )||p_{\theta }(\mathbf {z} ))-\mathbb {E} _{q_{\phi }(\mathbf {z} |\mathbf {x} )}{\big (}\log p_{\theta }(\mathbf {x} |\mathbf {z} ){\big )}

$D_{KL}$ note la divergence de Kullback-Leibler. L'a priori sur les variables latentes est habituellement défini comme une gaussienne multivariée isotrope centrée $p_{\theta }(\mathbf {z} )={\mathcal {N}}(\mathbf {0,I} )$ . Des configurations alternatives sont possibles^[17].

Auto-encodeur contractif[modifier | modifier le code]

L'auto-encodeur contractif ajoute une régularisation explicite dans sa fonction objectif qui force le modèle à apprendre une fonction robuste aux légères variations des valeurs d'entrées. Cette régularisation correspond à la norme de Frobenius de la matrice Jacobienne des activations de l'encodeur par rapport à l'entrée. La fonction objectif finale à la forme suivante :

{\mathcal {L}}(\mathbf {x} ,\mathbf {x'} )+\lambda \sum _{i}||\nabla _{x}h_{i}||^{2}

Relation avec la décomposition en valeurs singulières tronquée[modifier | modifier le code]

Si des activations linéaires sont utilisées, ou uniquement une seule couche cachée sigmoïde, la solution optimale d'un auto-encodeur est apparentée à une analyse en composantes principales^[18].

Apprentissage[modifier | modifier le code]

L'algorithme d'apprentissage d'un auto-encodeur peut être résumé comme suit :

Pour chaque entrée

x

,

Effectuer un passage vers l'avant afin de calculer les activations sur toutes les couches cachées, puis sur la couche de sortie pour obtenir une sortie

\mathbf {x'}

,

Mesurer l'écart entre

\mathbf {x'}

et l'entrée

\mathbf {x}

, généralement en utilisant l'erreur quadratique,

Rétropropager l'erreur vers l'arrière et effectuer une mise à jour des poids.

Un auto-encodeur est bien souvent entrainé en utilisant l'une des nombreuses variantes de la rétropropagation, e.g., méthode du gradient conjugué, algorithme du gradient. Bien que cela fonctionne de manière raisonnablement efficace, il existe des problèmes fondamentaux concernant l'utilisation de la rétropopagation avec des réseaux possédant de nombreuses couches cachées. Une fois les erreurs rétropropagées aux premières couches, elles deviennent minuscules et insignifiantes. Cela signifie que le réseau apprendra presque toujours à reconstituer la moyenne des données d'entrainement. Bien que les variantes de la rétropropagation soient capables, dans une certaine mesure, de résoudre ce problème, elles résultent toujours en un apprentissage lent et peu efficace. Ce problème peut toutefois être résolu en utilisant des poids initiaux proches de la solution finale. Le processus de recherche de ces poids initiaux est souvent appelé pré-entrainement.

Geoffrey Hinton a développé une technique de pré-entrainement pour l'auto-encodeur profond. Cette méthode consiste à traiter chaque ensemble voisin de deux couches comme une machine de Boltzmann restreinte de sorte que le pré-entrainement s'approche d'une bonne solution, puis utiliser la technique de rétropropagation pour affiner les résultats^[19]. Ce modèle porte le nom de réseau de croyance profonde.

Références[modifier | modifier le code]

↑ Tian, X., « Pré-apprentissage supervisé pour les réseaux profonds », In Proceedings of Rfia,‎ 2010, Vol. 2010, p. 36
↑ ^{a et b} (en) Y. Bengio, « Learning Deep Architectures for AI », Foundations and Trends in Machine Learning, vol. 2,‎ 2009 (DOI 10.1561/2200000006, lire en ligne)
↑ Modeling word perception using the Elman network, Liou, C.-Y., Huang, J.-C. and Yang, W.-C., Neurocomputing, Volume 71, 3150–3157 (2008), DOI 10.1016/j.neucom.2008.04.030
↑ Autoencoder for Words, Liou, C.-Y., Cheng, C.-W., Liou, J.-W., and Liou, D.-R., Neurocomputing, Volume 139, 84–96 (2014), DOI 10.1016/j.neucom.2013.09.055
↑ ^{a et b} Auto-Encoding Variational Bayes, Kingma, D.P. and Welling, M., ArXiv e-prints, 2013 arxiv.org/abs/1312.6114
↑ Generating Faces with Torch, Boesen A., Larsen L. and Sonderby S.K., 2015 torch.ch/blog/2015/11/13/gan.html
↑ ^{a et b} (en) Nathalie Japkowicz, Stephen José Hanson et Mark A. Gluck, « Nonlinear Autoassociation Is Not Equivalent to PCA », Neural Computation, vol. 12, n^o 3,‎ 1^er mars 2000, p. 531–545 (ISSN 0899-7667 et 1530-888X, DOI 10.1162/089976600300015691, lire en ligne, consulté le 18 avril 2023)
↑ Holger Schwenk et Yoshua Bengio, « Méthodes d'entraînement pour la stimulation adaptative des réseaux de neurones », Advances in Neural Information Processing Systems, MIT Press, 1997
↑ Jürgen Schmidhuber, « Deep learning in réseaux de neurones : un aperçu », Réseaux de neurones, janvier 2015 (PMID 25462637, DOI 10.1016/j.neunet.2014.09.003, arXiv 1404.7828, S2CID 11715509), p. 85–117
↑ Hinton, G.E., & Zemel, R.S. (1994). Auto-encodeurs, longueur de description minimale et énergie libre de Helmholtz. Dans Advances in neural information processing systems 6 (p. 3-10).
↑ (en) Diederik P Kingma et Max Welling, « Auto-Encoding Variational Bayes », 2013.
↑ Générer des visages avec Torch, Boesen A., Larsen L. et Sonderby S.K., 2015 torch.%20ch/blog/2015/11/13/gan.html
↑ Pedro Domingos, The master algorithm : how the quest for the ultimate learning machine will remake our world, 2015 (ISBN 978-0-465-06570-7, 0-465-06570-8 et 978-0-465-09427-1, OCLC 900623914, lire en ligne)
↑ (en) Pascal Vincent, Hugo Larochelle, Isabelle Lajoie, Yoshua Bengio et Pierre-Antoine Manzagol, « Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion », The Journal of Machine Learning Research, vol. 11,‎ 2010, p. 3371–3408 (lire en ligne)
↑ (en) « Sparse autoencoder »
↑ Alireza Makhzani et Brendan Frey, « k-Sparse Autoencoders », arXiv:1312.5663 [cs],‎ 19 décembre 2013 (lire en ligne, consulté le 23 mai 2017)
↑ Harris Partaourides and Sotirios P. Chatzis, “Asymmetric Deep Generative Models,” Neurocomputing, vol. 241, p. 90-96, June 2017. [1]
↑ (en) H. Bourlard et Y. Kamp, « Auto-association by multilayer perceptrons and singular value decomposition », Biological Cybernetics, vol. 59, n^os 4–5,‎ 1988, p. 291–294 (PMID 3196773, DOI 10.1007/BF00332918)
↑ Reducing the Dimensionality of Data with Neural Networks (Science, 28 July 2006, Hinton & Salakhutdinov)

Voir aussi[modifier | modifier le code]

Articles connexes[modifier | modifier le code]

[1] Tian, X., « Pré-apprentissage supervisé pour les réseaux profonds », In Proceedings of Rfia,‎ 2010, Vol. 2010, p. 36

[bengio-2] {a et b} (en) Y. Bengio, « Learning Deep Architectures for AI », Foundations and Trends in Machine Learning, vol. 2,‎ 2009 (DOI 10.1561/2200000006, lire en ligne)

[3] Modeling word perception using the Elman network, Liou, C.-Y., Huang, J.-C. and Yang, W.-C., Neurocomputing, Volume 71, 3150–3157 (2008), DOI 10.1016/j.neucom.2008.04.030

[4] Autoencoder for Words, Liou, C.-Y., Cheng, C.-W., Liou, J.-W., and Liou, D.-R., Neurocomputing, Volume 139, 84–96 (2014), DOI 10.1016/j.neucom.2013.09.055

[VAE-5] {a et b} Auto-Encoding Variational Bayes, Kingma, D.P. and Welling, M., ArXiv e-prints, 2013 arxiv.org/abs/1312.6114

[gan_faces-6] Generating Faces with Torch, Boesen A., Larsen L. and Sonderby S.K., 2015 torch.ch/blog/2015/11/13/gan.html

[Nonlinear_Autoassociation_Is_Not_Equivalent_to_PCA-7] {a et b} (en) Nathalie Japkowicz, Stephen José Hanson et Mark A. Gluck, « Nonlinear Autoassociation Is Not Equivalent to PCA », Neural Computation, vol. 12, n^o 3,‎ 1^er mars 2000, p. 531–545 (ISSN 0899-7667 et 1530-888X, DOI 10.1162/089976600300015691, lire en ligne, consulté le 18 avril 2023)

[8] Holger Schwenk et Yoshua Bengio, « Méthodes d'entraînement pour la stimulation adaptative des réseaux de neurones », Advances in Neural Information Processing Systems, MIT Press, 1997

[9] Jürgen Schmidhuber, « Deep learning in réseaux de neurones : un aperçu », Réseaux de neurones, janvier 2015 (PMID 25462637, DOI 10.1016/j.neunet.2014.09.003, arXiv 1404.7828, S2CID 11715509), p. 85–117

[10] Hinton, G.E., & Zemel, R.S. (1994). Auto-encodeurs, longueur de description minimale et énergie libre de Helmholtz. Dans Advances in neural information processing systems 6 (p. 3-10).

[VAE2-11] (en) Diederik P Kingma et Max Welling, « Auto-Encoding Variational Bayes », 2013.

[gan_faces2-12] Générer des visages avec Torch, Boesen A., Larsen L. et Sonderby S.K., 2015 torch.%20ch/blog/2015/11/13/gan.html

[13] Pedro Domingos, The master algorithm : how the quest for the ultimate learning machine will remake our world, 2015 (ISBN 978-0-465-06570-7, 0-465-06570-8 et 978-0-465-09427-1, OCLC 900623914, lire en ligne)

[ref9-14] (en) Pascal Vincent, Hugo Larochelle, Isabelle Lajoie, Yoshua Bengio et Pierre-Antoine Manzagol, « Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion », The Journal of Machine Learning Research, vol. 11,‎ 2010, p. 3371–3408 (lire en ligne)

[15] (en) « Sparse autoencoder »

[16] Alireza Makhzani et Brendan Frey, « k-Sparse Autoencoders », arXiv:1312.5663 [cs],‎ 19 décembre 2013 (lire en ligne, consulté le 23 mai 2017)

[17] Harris Partaourides and Sotirios P. Chatzis, “Asymmetric Deep Generative Models,” Neurocomputing, vol. 241, p. 90-96, June 2017. [1]

[18] (en) H. Bourlard et Y. Kamp, « Auto-association by multilayer perceptrons and singular value decomposition », Biological Cybernetics, vol. 59, n^os 4–5,‎ 1988, p. 291–294 (PMID 3196773, DOI 10.1007/BF00332918)

[19] Reducing the Dimensionality of Data with Neural Networks (Science, 28 July 2006, Hinton & Salakhutdinov)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]