Algorithme de parcours en largeur
Pour les articles homonymes, voir BFS.L'algorithme de parcours en largeur (ou BFS, pour Breadth First Search) permet le parcours d'un graphe de manière itérative, en utilisant une file. Il peut par exemple servir à déterminer la connexité d'un graphe.
Sommaire |
[modifier] Principe
Cet algorithme diffère de l'algorithme de parcours en profondeur par le fait que, à partir d'un sommet S, il liste d'abord les voisins de S pour ensuite les explorer un par un. Ce mode de fonctionnement utilise donc une file dans laquelle il prend le premier sommet et place en dernier ses voisins non encore explorés.
Lorsque l'algorithme est appliqué à un graphe quelconque, les sommets déjà visités doivent être marqués afin d'éviter qu'un même sommet soit exploré plusieurs fois. Dans le cas particulier d'un arbre, ce n'est pas nécessaire.
Étapes de l'algorithme :
- Mettre le nœud de départ dans la file.
- Retirer le nœud du début de la file pour l'examiner.
- Mettre tous les voisins non examinés dans la file (à la fin).
- Si la file n'est pas vide reprendre à l'étape 2.
[modifier] Pseudo code
BFS(graphe G, sommet s):
{
f = CreerFile();
Marquer(s);
Enfiler(f, s);
TANT-QUE NON FileVide(f) FAIRE
x = Défiler(f);
Afficher(x)
TANT-QUE ExisteFils(x) FAIRE
z = FilsSuivant(x);
SI NonMarqué(z) ALORS
Marquer(z);
Enfiler(f, z);
FIN-SI
FIN-TANT-QUE
FIN-TANT-QUE
}
[modifier] Exemple
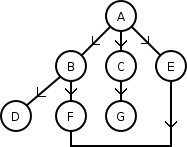
Sur le graphe suivant, cet algorithme va alors fonctionner ainsi :
Il explore dans l'ordre les sommets A, B, C, E, D, F, G, contrairement à l'algorithme de parcours en profondeur qui cherche dans cet ordre : A, B, D, F, C, G, E.
[modifier] Applications
Le parcours en largeur explore tous les sommets accessibles depuis le sommet initial. Il permet de calculer les composantes connexes du graphe avec une complexité linéaire.
De plus, lors de ce parcours, les sommets sont explorés par distance croissante au sommet de départ. Grâce à cette propriété, on peut utiliser l'algorithme pour résoudre le plus simple des problèmes de cheminement : calculer le plus court chemin entre deux sommets dans un graphe non pondéré.
